книги / Основы биомеханики

В результате наложенная деформация, свободная от напряжений, ε*u , становится равной полной деформации ε1 и наложенная нильпотентная собственная деформация ε*σ дает нулевую полную деформацию ε2 .

9.9. ФУНКЦИОНАЛЬНОЕ ПРОСТРАНСТВО СОБСТВЕННЫХ ДЕФОРМАЦИЙ

Дальнейшее изложение теории собственных напряжений и деформаций становится более наглядным при введении функционального пространства собственных деформаций. Это пространство аналогично трехмерному евклидову пространству E3 , элементами его являются не геометрические точки, как в E3 , а функции – собственные деформации. Основное свойство пространства заключается в свойстве линейности, то есть в том, что сложение элементов пространства (то есть собственных деформаций) и умножение на скаляр (число) вновь дает некоторый элемент этого пространства (то есть некоторую собственную деформацию). По аналогии с про-

141

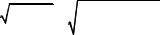
странством E3 в пространстве собственных деформаций вводится скалярное произведение элементов и норма элемента (аналог модуля вектора).

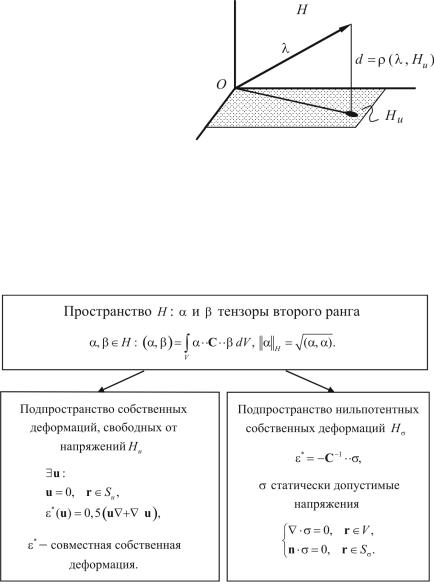
Пусть H − множество симметричных тензоров второго ранга. Тензоры α и β − элементы этого множества. Скалярное произведение элементов вводится по формуле

что имеет место для произвольых элементов множества собственных деформаций H .

Отметим, что введенное функциональное пространство симметричных тензоров называют также энергетическим пространством H.

9.9.1. Подпространство совместных деформаций

По определению, симметричный тензор λ H принадлежит подпространству Hu , если существует такая вектор-функция u , что

Подпространство Hu является линейным пространством, так как суммирование элементов в Hu и умножение на скаляр дает также элемент подпространства Hu .

Условие ε* Hu есть необходимое и достаточное условие того, что собственная деформация является свободной от напряжений.

Полученное подпространство Hu является подпространством совместных деформаций с дополнительным условием u = 0, r Su .

142

9.9.2. Подпространства совместных деформаций, свободных от напряжений, и нильпотентных собственных деформаций

Рис. 9.7. Функциональные пространства собственных деформаций

143

Таким образом, собственная деформация ε* свободна от напряжений тогда и только тогда, когда она совместна с дополнительным условием u = 0, r Su , т.е. принадлежит подпространству Hu .

Собственная деформация ε* нильпотентна тогда и только тогда, когда соответствующие напряжения статически допустимы (собственные напряжения), т.е. удовлетворяют уравнению равновесия с нулевыми объемными силами и нулевым вектором поверхностного напряжения. Множество нильпотентных собственных деформаций образует линейное подпространство Hσ . Иллюстрация функцио-

нальных пространств H , Hu , Hσ приведена на рис. 9.7.

9.10. ТЕОРЕМАОДЕКОМПОЗИЦИИСОБСТВЕННОЙ ДЕФОРМАЦИИ

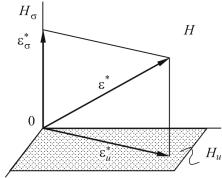
Любой тензор собственной деформации ε* H , существующей в теле, может быть разложен единственным образом на две части, а именно: на собственную деформацию, свободную от напряжений, и нильпотентную собственную деформацию

144

После проведения декомпозиции можно вычислить полную деформацию и напряжения, вызванные имеющейся собственной деформацией:

9.10.1. Доказательство возможности декомпозиции

Рассмотрим некоторое распределение собственной деформации ε* , существующее в теле. Оно производит упругую деформацию εe иполную деформацию ε.

венная деформация, не вызывающая напряжений в любой точке тела. Собственная деформация (−ε*u ) имеет аналогичные свойства. После

Из формулы (9.54) можно заключить, что наложенная собственная деформация ε*σ приводит к состоянию, свободному от деформа-

ций, и поэтому эта собственная деформация является нильпотентной. Соотношение (9.53) можно записать несколько в ином виде:

где ε*u Hu , ε*σ Hσ . Врезультате, исходнаясобственнаядеформация ε* оказаласьразложеннойсогласноутверждениютеоремыодекомпозиции.

145

9.10.2. Доказательство единственности

На втором шаге покажем, что декомпозиция единственна. Для доказательства предположим от противного, что декомпозиция суще-

Из постановок краевых задач для собственных деформаций, свободных от напряжений (9.43), и для нильпотентных собственных деформаций (9.44) сразу следует, что единственный элемент, который принадлежит обоим подпространствам Hu и Hσ , это только ну-

и декомпозиция является единственной.

Наконец, покажем, что подпространства Hu и Hσ взаимно ортогональны, т.е. любые тензорные элементы ε*u Hu и ε*σ Hσ вза-

имно ортогональны. Другими словами, их скалярное произведение равно нулю.

146

(ε*u ,ε*σ ) = ∫ε*u C ε*σ dV = −∫ε(u) σdV =

Можно сделать вывод, что существует ортогональная декомпо-

Теорема утверждает, что любая собственная деформация, существующая в теле, может быть единственным образом разложена на две составляющие: собственную деформацию, свободную от напряжений, и нильпотентную собственную деформацию. В частности, температурная деформация имеет такое же свойство, и это тоже важно для анализа температурных напряжений и деформаций.

Декомпозиция собственных деформаций предоставляет важную для практики возможность полностью разделить управление напряжениями и деформациями, производимыми силовым нагружением.

9.11. ПРИМЕР ДЕКОМПОЗИЦИИ

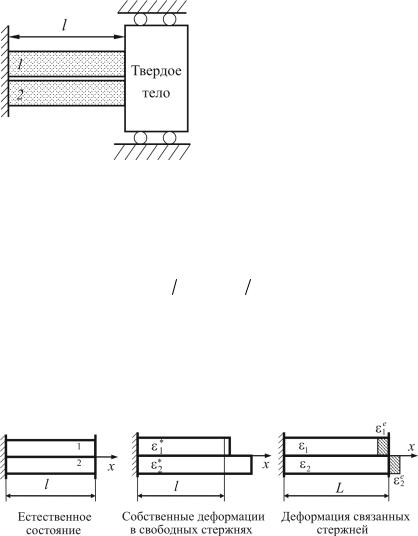
Два стержня с одинаковым модулем упругости E и поперечным сечением A в процессе деформации имеют одинаковую длину l

(рис. 9.9).

147

деформацию, свободную от напряжений, и нильпотентную собственную деформации.

в нашем иллюстрированном примере (рис. 9.10) мы имеем

σ1 > 0, σ2 < 0 .

Рис. 9.10. Схема деформаций

Теперь определим подпространства Hu и Hσ для рассматриваемой системы. Из уравнения (9.63) видно, что для собственной де-

148

формации, свободной от напряжений ( σ1 = σ2 = 0 ), мы получаем соотношение ε1*u = ε*2u . Следовательно, любая собственная деформация, свободная от напряжений, имеет вид

Для нильпотентной собственной деформации имеем (в соответствии с определением нильпотентной собственной деформации)

Из соотношения (9.64) следует, что

или любая нильпотентная собственная деформация имеет вид

Элементы ε*u и ε*σ взаимно ортогональны. В самом деле,

(ε*u ,ε*σ ) = ∫ε*u C ε*σ dV = ∑2 ε*i u E ε*i σli A =

V i =1

= E Al (ε* ε*σ + ε* ε* σ ) = E Al M N (1 1 −1 1) = 0 .

1u 1 2u 2

Далее покажем, что в результате реализована декомпозиция собственной деформации ε* ={ε1* , ε*2 } на составляющие: собственную

деформацию, свободную от напряжений, и нильпотентную собственную деформацию. Другими словами, имеет место соотношение

ε* = ε*u +ε*σ ,

или

{ε1* , ε*2 } = M {1;1} + N {1; −1} .

149

Запишем два уравнения с двумя неизвестными коэффициентами M и N .

В результате мы можем записать разложение собственной деформации на две составляющие:

формация.

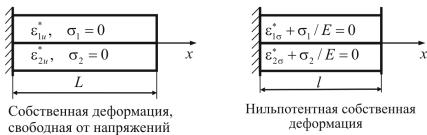
Конфигурация системы при этих собственных деформациях показана на рис. 9.11.

Рис. 9.11. Конфигурация системы при собственной деформации, свободной от напряжений, и нильпотентной собственной деформации

150