
книги / Несущая способность конструкций в условиях теплосмен
..pdf
Dx = f − (A1 + A2 )x,
и формула метода Якоби будет выглядеть следующим образом:
Dx(s+1) = f − (A + A )x(s) . |
|
1 |
2 |
Учитывая, что A1 + A2 = A − D , |
последнее выражение можно |
также представить в форме
D(x(s+1) − x(s) ) + Ax(s) = f .
11.1.3. Метод Зейделя
Для метода Зейделя58 выражение
|
|
i−1 |
m |
xi(s+1) |
= fi − ai j x(js+1) |
− ai j x(js) |
|
|
|
j=1 |
j=i+1 |
(7.1) преобразуется к виду
|
|
|
|
|
ai i , aii ≠ 0, i = 1,m , |
||||
|
||||
|
|
|
|
|
где s – номер итерации. В отличие от метода Якоби, для вычисления
очередной неизвестной xi(s +1) |
на s + 1 итерации используются все |
||
предварительно найденные |
на той же итерации величины |
||
x(js+1) , j = |
|
. Как и ранее, |
вычислительный процесс заканчивает- |
1,i − 1 |
|||
ся, когда выполняется условие
max x(js+1) − x(js) < δ,
1≤ j≤m
где δ – заданная погрешность вычисления результата, δ > 0.
Пример. Решить систему линейных алгебраических уравнений
4x1 + 2x2 = 5,3x1 + 5x2 = 9
методом Зейделя. Точное решение этой системы: x1 = 0,5, x2 = 1,5.
58Зейдель Филипп Людвиг (24.10.1821–13.08.1896) – немецкий астроном
иматематик, член Баварской и Геттингенской академий наук.
131

Уравнения системы записываются в виде итерационной схемы Зейделя:
|
|
|
(s+1) |
(s) |
) |
4, |
|
|
|
|
x1 |
= (5 − 2x2 |
|
|
|||
|
|
|
|
= (9 − 3x1(s+1) ) |
|
|
|
|
|
|
x2(s+1) |
5. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Это означает, что для нахождения |
x2( s+1) на s + 1 итерации ис- |
||||||
пользуется значение x( s+1) |
, вычисленное ранее на той же s + 1 ите- |
|||||||
|
1 |
|
|
|
|
|
|
|
рации. В качестве начального приближения принимаются |
x(0) = 0 , |
|||||||
|
|
|
|
|
|
|
|
1 |
x(0) |
= 0 . |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 11.2 |
|
|
Результаты выполнения итераций метода Зейделя |
|
||||||
|
|
|
|
|
|
|
|
|
|
s |
|
|
x1(s) |
|
|
x2(s) |
|
|
0 |
|
|
|
|
|
0 |
|
|
1 |
|
|
1,25 |
|
|
|
|
|
|
|
|
|
|
|
1,05 |
|
|
2 |
|
|
0,725 |
|
|
|
|
|
|
|
|
|
|
|
1,365 |
|
|
3 |
|
|
0,5675 |
|
|
|
|
|
|
|
|
|
|
|
1,4595 |
|
|
4 |
|
|
0,5203 |
|
|
|
|
|
|
|
|
|
|
|
1,4879 |
|
|
5 |
|
|
0,5061 |
|
|
|
|
|
|
|
|
|
|
|
1,4964 |
|
|
6 |
|
|
0,5018 |
|
|
|
|
|
|
|
|
|
|
|
1,4989 |
|
|
7 |
|
|
0,5005 |
|
|
|
|
|
|
|
|
|
|
|
1,4997 |
|
Ход выполнения итерационного процесса Якоби отображен на рис. 11.2, результаты расчетов приведены в табл. 11.2. После выпол-
нения семи итераций |
|
x(7) − x(6) |
|
= 0,0013, |
|
x(7) − x(6) |
|
= 0,0008 . Ис- |
||
|
|
|
|
|||||||
|
|
1 |
1 |
|
|
|
2 |
2 |
|
|
пользуемая оценка показывает, что решение методом Зейделя также получено с погрешностью не более 0,0015.
132
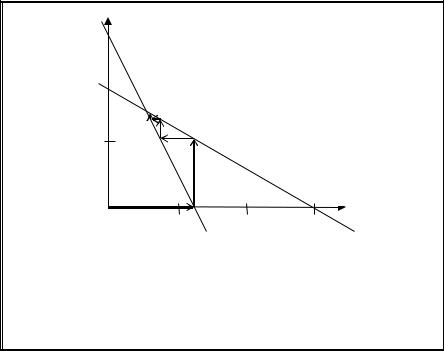
x2
2 |
|
|
4x1 + 2 x2 = 5 |
|
|
|
|
1
3x1 + 5 x2 = 9
x1
0 |
1 |
2 |
3 |
Рис. 11.2. Схема выполнения итераций метода Зейделя
В действительности точное решение системы и решение, полученное методом Зейделя после тринадцати итераций, различаются не более чем на 0,0005. Очевидно, что метод Зейделя дает последовательность, быстрее сходящуюся к точному решению.
Как и в предыдущем случае, матрица коэффициентов А представляется в виде суммы A = A1 + D + A2 с теми же обозначениями. Итерационную формулу метода Зейделя можно представить в форме
( A1 + D ) x(s+1) = f − A2 x(s).
Учитывая, как и ранее, что A2 = A − A1 − D , последнее выражение можно записать в виде итерационной схемы
( A1 + D)(x(s+1) − x(s) )+ Ax(s) = f .
11.1.4. Сходимость итерационных методов
Сравнивая формулы метода Якоби,
D(x(s+1) − x(s) ) + Ax(s) = f ,
133

и метода Зейделя,
( A1 + D)(x(s+1) − x(s) )+ Ax(s) = f ,
можно отметить, что если последовательности получаемых решений сходятся, то есть в некотором смысле x(s+1) − x(s) → 0, s → ∞ , то они
сходятся к решению исходных задач Ax(s ) = f . Однако возможна
ситуация, когда сходимость последовательности получаемых решений отсутствует.
Пример. Решить систему линейных алгебраическихуравнений
4x1 + 2x2 = 5,−20x1 + 5x2 = −2,5.
Точное решение этой системы алгебраических уравнений из-
вестно: x1 = 0,5, x2 = 1,5 .
Таблица 11.3
Отсутствие сходимости решения системы линейных алгебраических уравнений при применении метода Зейделя
s |
x(s ) |
x(s ) |
|
1 |
2 |
0 |
|
0,0 |
1 |
1,25 |
|
|
|
4,5 |
2 |
–1,0 |
|
|
|
–4,5 |
3 |
3,5 |
|
|
|
13,5 |
4 |
–5,5 |
|
|
|
–22,5 |
5 |
12,5 |
|
|
… |
49,5 |
Для нахождения решения используется итерационный метод Зейделя. Как и ранее, уравнения системы записываются в виде итерационной схемы:
134
|
|
|
|
(s+1) |
|
|
|
|
(s) |
) |
4, |
|
|
|
|
|
|
|
|
|
x1 |
= (5 − 2x2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
= (−2,5 + 20x1(s+1) ) |
|
|
|
|
|||||||
|
|
|
x2(s+1) |
|
5. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
x2 |
–20x1 + 5x2 = –2,5 |
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
3 |
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
–5 |
–4 |
–3 |
–2 |
–1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–3 |
|
|
|
4x1 + 2x2 = 5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
–4 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
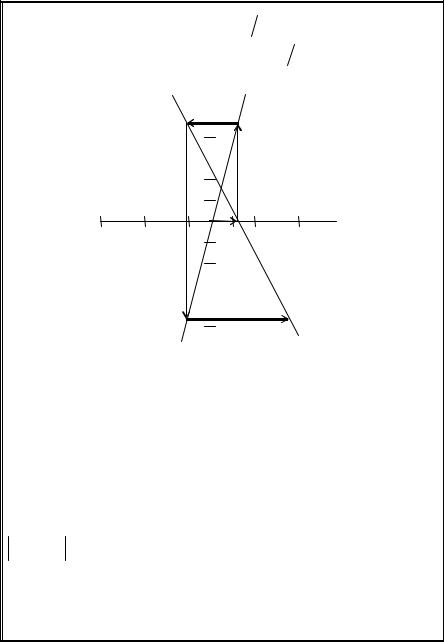
Рис. 11.3. Отсутствие сходимости при использовании метода Зейделя
Результаты вычислений представлены в табл. 11.3. На рис. 11.3 показан ход выполнения итерационной процедуры Зейделя.
Расчеты показывают, что в рассматриваемом примере отсутствует сходимость последовательности получаемых решений: с увели-
чением количества итераций x(s+1) − x(s) → ∞, s → ∞ . |
|
|
|
|
|
|||
После |
выполнения |
пяти |
итераций |
|
x(5) − x(4) |
|
= 18 , |
|
|
|
|||||||
|
|
|
|
|
1 |
1 |
|
|
x2(5) − x2(4) = 72 , причем с увеличением номера итерации различие
между найденными результатами увеличивается. Понятно, что итерационная процедура решения заданной системы алгебраических уравнений не позволяет получить последовательность решений, сходящуюся к какому-либо результату.
135

|
|
11.2. Нелинейные уравнения |
|
|
|
Предполагается, |
что задана нелинейная зависимость вида |
||
y = |
f(x). |
Требуется |
определить все те значения |
аргумента |
xk , |
k =1, |
2, , которые обращают функцию в нуль: |
|
|
|
|
|
f (xk ) = 0. |
(11.3) |
Для поиска корней нелинейных уравнений, как правило (за небольшим исключением: квадратные, кубические, некоторые трансцендентные уравнения), используются итерационные методы.
11.2.1. Метод половинного деления59
Метод основан на теореме математического анализа [3]: функция, непрерывная в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в нуль внутри интервала.
Предполагается, что функция f(x) непрерывна в замкнутом интервале [x0 , x1 ]. Метод заключается в последовательном сокращении
длины этого интервала для локализации корня уравнения (11.3). Первоначально проверяются значения заданной функции на концах интервала. В случае если
f (x(0) ) f (x(1) ) = 0 ,
один из концов интервала является искомым корнем уравнения. Если на концах интервала значения функции имеют разные
знаки, то имеет место соотношение
|
f (x(0) ) f (x(1) )< 0 . |
В этом случае вычисляется значение аргумента в середине ин- |
|
тервала |
(x(0) + x(1) ) 2 , и вычисляется значение функции |
f (x(2) ) |
в этой точке. Далее сравниваются знаки функции в точке |
59 Встречаются иные названия этого метода: метод бисекции, дихотомии.
136
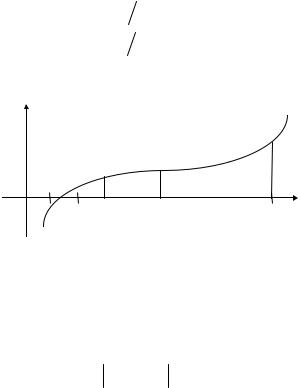
x(2) и, например, в левой точке x(0) интервала. Если имеет место соотношение f (x(0) ) f (x(2) )< 0 (рис. 11.4), то корень следует искать
винтервале x(0) , x(2) . В противном случае корень разыскивается
винтервале x(2) , x(1) . В результате выполненной операции исход-
ный интервал сократился вдвое.
Далее в зависимости от ситуации интервал вновь делится пополам:
(x(2) + x(0) ) 2, x(3) =
(x(2) + x(1) ) 2,
и т.д.
f (x(2) ) f (x(0) )< 0; f (x(2) ) f (x(0) ) > 0,
f(x1)
f(x4) f(x3) f(x2)
x |
x |
|
x |
|
x |
x |
|
|
Рис. 11.4. Схема метода половинного деления
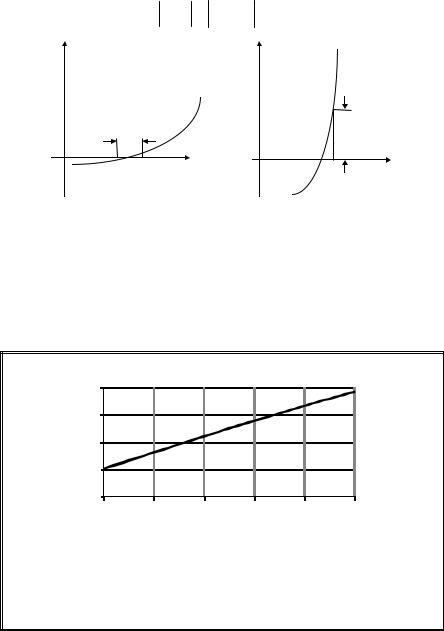
Для прекращения вычислительной процедуры могут применяться различные критерии. Если функция достаточно пологая, имеет смысл использовать условие малости интервала, ограничивающего положение корня (рис. 11.5, a):
x(s+1) − x(s) < δx .
Если функция «круто» меняет свое значение, целесообразно применять условие (рис. 11.5, б) «близости» значения функции f(x) к нулевому значению:
137
|
|
y(s+1) = f (x(s) ) < δy . |
|
||
δx |
|
|
|
|
δy |
|
|
|
|
|
|
xk |
xk+1 |
|
|
xk |
|
a |
|
|
|
б |
|
Рис. 11.5. Частные случаи поиска корня нелинейного уравнения: |
|||||
а – пологая функция; б – функция «круто» меняет значение |
|||||
Если заранее неизвестен характер «поведения» функции, име- |
|||||
ет смысл использовать одновременно оба условия для остановки |
|||||
итерационного процесса. |
|
|
|
||
Пример. Найти корень уравнения 2x + sin х − 1 = 0 . |
|||||
2 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
–-1 |
|
|
|
|
|
–-2 |
|
|
|
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
Рис. 11.6. Функция |
f (x) = 2x + sin х − 1 |
|
|||
Вид функции |
f (x ) = 2x + sin х − 1 |
показан на рис. 11.6, из ко- |
|||
торого видно, что корень этого уравнения принадлежит интервалу |
|||||
[0, 1]. Рассматриваемая функция в этом интервале непрерывна и на |
|||||
138

его концах принимает значения разных знаков. Это означает, что для поиска корня заданного уравнения может быть использован метод половинного деления. Результаты расчетов приведены в табл. 11.4. Значение корня уравнения (с погрешностью не более 10–10): 0,335 418.
|
|
|
|
|
Таблица 11.4 |
|
|
Результаты вычисления корня уравнения 2x + sin (x) − 1 = 0 |
|
||||
|
|
методом половинного деления |
|
|
||
|
|
|
|
|
|
|
|
Номер |
Левая точка |
Центральная |
Правая точка |
Ширина |
|
|
итерации |
точка |
отрезка |
|
||
|
1 |
0,0 |
0,5 |
1,0 |
1,0 |
|
|
2 |
0,0 |
0,25 |
0,5 |
5,0 10–1 |
|
|
3 |
0,25 |
0,375 |
0,5 |
2,5 10–1 |
|
|
4 |
0,25 |
0,3125 |
0,375 |
1,25 10–1 |
|
|
5 |
0,3125 |
0,34 375 |
0,375 |
6,25 10–2 |
|
|
6 |
0,3125 |
0,328 125 |
0,343 75 |
3,125 10–2 |
|
|
7 |
0,328 125 |
0,335 937 5 |
0,343 75 |
1,5625 10–2 |
|
|
8 |
0,328 125 |
0,332 031 3 |
0,335 937 5 |
7,8125 10–3 |
|
|
9 |
0,332 031 3 |
0,333 984 4 |
0,335 937 5 |
3,9063 10–3 |
|
|
10 |
0,333 984 4 |
0,334 960 9 |
0,335 937 5 |
1,9531 10–3 |
|
|
11 |
0,334 960 9 |
0,335 449 2 |
0,335 937 5 |
9,7656 10–4 |
|
|
12 |
0,334 960 9 |
0,335 205 1 |
0,335 449 2 |
4,8828 10–4 |
|
|
13 |
0,335 205 1 |
0,335 327 1 |
0,335 449 2 |
2,4414 10–4 |
|
|
14 |
0,335 327 1 |
0,335 388 2 |
0,335 449 2 |
1,2207 10–4 |
|
|
15 |
0,335 388 2 |
0,335 418 7 |
0,335 449 2 |
6,1035 10–5 |
|
|
|
|
… |
|
|
|
|
36 |
0,335 418 0 |
0,335 418 0 |
0,335 418 0 |
2,9104 10–11 |
|
|
|
11.2.2. Метод простых итераций |
|
|
||
|
Метод простых |
итераций заключается в замене уравне- |
|
|||
|
ния (11.3) эквивалентным ему уравнением вида |
|
|
|||
x = ϕ (x).
Для приведения выражения (11.3) к требуемому виду можно воспользоваться простым приемом:
139
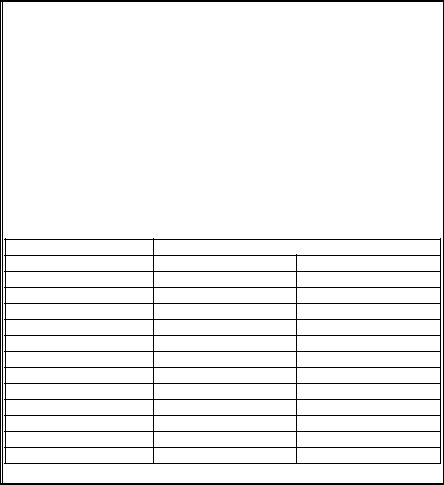
f(x) = f (x) + x − x = 0,
x= x + f (x) = ϕ (x).
Спомощью этой зависимости строится итерационный процесс
x(s+1) = ϕ(x(s) )
при некотором заданном начальном значении x(0) .
Пример. Найти корень уравнения 2x + sin х − 1 = 0 методом простых итераций. Уравнение преобразуется к стандартному виду
x= [1 − sin х]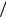 2
2
ик форме итерационного процесса
x(s+1) = 1− sin x(s) 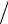 2.
2.
Результаты расчетов даны в табл. 11.5.
Таблица 11.5
Результаты вычисления корней уравнения 2x + sin х − 1 = 0 методом простых итераций при разных начальных значениях x(0)
Номер итерации |
Приближения решения |
|
0 |
x(0) = 0,0 |
x(0) = 1,0 |
1 |
0,5 |
0,079 264 5 |
2 |
0,260 287 2 |
0,460 409 2 |
3 |
0,371 320 9 |
0,277 842 6 |
4 |
0,318 576 7 |
0,362 859 2 |
5 |
0,343 392 4 |
0,322 525 7 |
6 |
0,331 658 3 |
0,341 518 5 |
7 |
0,337 194 3 |
0,332 540 9 |
8 |
0,334 579 7 |
0,336 777 1 |
9 |
0,335 813 9 |
0,334 776 5 |
10 |
0,335 231 1 |
0,335 721 0 |
… |
… |
… |
30 |
0,335 418 0 |
0,335 418 0 |
140
