Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Несущая способность конструкций в условиях теплосмен

..pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

4.03 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Для этого используется ряд математических преобразований с использованием формулы Коши (8.1) и теоремы Остроградского43– Гаусса44. Уравнения движения (8.4) являются справедливыми для движения всех видов сплошной среды: твердых деформируемых тел, жидкостей и газов.

8.4. Закон сохранения энергии

Изменение полной энергии массы жидкости в объеме V за промежуток времени dt происходит за счет работы поверхностных p и массовых f сил, за счет притока за тот же промежуток времени тепловой энергии вследствие наличия объемно распределенных источников тепла q, а также теплового потока J через поверхность (см. рис. 8.2) за счет теплопроводности.

Закон сохранения энергии, записанный для бесконечно малой материальной частицы, выражается соотношением

dU = dAV + dAS + dQV + dQS .

В этом выражении обозначено:

	v2
U = ρ		2	+ E dV
V

– полная энергия среды в объеме V, равная сумме кинетической энергии ρv2dV/2 и внутренней энергии ρEdV всех входящих в этот объем материальных частиц;

dAV = ρf (vdt )dV

– элементарная работа массовых сил f, приложенных к материальной частице массой ρdV, на перемещении vdt;

43Остроградский Михаил Васильевич (12.09.1801–20.12.1861) – российский математик и механик, академик Санкт-Петербургской академии наук, признанный лидер математиков Российской империи в 30–60-е гг. XIX в.

44Гаусс Карл Фридрих (30.04.1777–23.02.1855) – немецкий ученый-матема- тик, учился и работал в Геттингенском университете, Университете Брауншвейга, Геттингенском университете, Геттингенской астрономической обсерватории. Иностранный почетный член Петербургской академии наук.

dAS = p (vdt)dS

– элементарная работа поверхностных сил p, действующих на поверхностьматериальной частицы площадью dS, на перемещенииvdt;

dQV = (qdt )dV

– поступление энергии в объем dV за счет внутренних источников, имеющих мощность q, за время dt;

dQS = (Jdt) ndS

– поступление энергии c вектором J потока тепла через поверхность с нормалью n и площадью dS материальной частицы за время dt за счет теплопроводности среды.

Подстановка составляющих в закон сохранения энергии:

+ E

= ρf (vdt )dV

+ p (vdt )dS + dt qdV + dt J ndS ,

d ρ

приводит к интегральной

+ E dV

− ρ

+ E dV

= ρf vdVdt + p vdSdt + qdVdt +

J ndSdt

t0 V

t0 S

t0 V

t0 S

и дифференциальной

+ E dV = ρf vdV + p vdS + qdV + J ndS

dt V

формам закона: скорость изменения полной энергии U сплошной среды, заключенной в объеме V, равна сумме мощностей объемных f и поверхностных p сил, а также объемного поступления энергии за счет внутренних источников мощностью q и потока тепла J через поверхность этого объема.

Применение формулы Коши (8.1), уравнения неразрывности (8.2), уравнения движения (8.4) и соотношения теоремы Остроградского – Гаусса приводит к еще одной дифференциальной форме закона сохранения энергии:

ρdEdt = σ : gradv + q + divJ .

Вэтом выражении используются символ двойного скалярного произведения «:» и математическая операция определения градиента вектора скорости:

gradv = ∂∂vx i + ∂∂vx j + ∂∂vx k .

8.5. Уравнение теплопроводности

Для получения уравнения теплопроводности принимается гипотеза о том, что для теплопроводной сплошной среды внутренняя энергия пропорциональна температуре:

E = cT ,

и выполняется закон Фурье

J = ηgrad T ,

где c, η – коэффициенты теплоемкости и теплопроводности среды; Т – температурное поле. В этом случае дифференциальная форма закона сохранения энергии приводится к виду уравнения теплопро-

водности

cρ dTdt = σ : gradv + q + div(ηgrad T ) ,

или в координатной форме

cρ

∂

∂T

∂

∂T

∂

∂T

+ q + Φ .

(8.5)

∂x

∂y

∂z

В выражении (8.5) введено обозначение

Φ = σ

∂v

+ σ

∂v

+ σ

∂v

+ σ

∂vy

xx ∂x

∂y

yx ∂x

∂z

+ σ

∂vy

+ σ

∂vy

+ σ

∂v

+ σ

∂v

+ σ

∂v

z .

yy ∂y

∂z

∂y

∂x

∂z

8.6. Уравнение состояния

Для жидкости и газа в общем случае плотность ρ зависит от давления p и температуры T. Соответствующая зависимость p (ρ,T )

или ρ ( p,T ) , связывающая указанные параметры, называется урав-

нением состояния жидкости и газа. Для идеальных (в термодинамическом смысле) жидкостей и газов таким уравнением состояния является закон Менделеева45 – Клайперона46

pV = mβ RT ,

где β – молярная масса среды; R – универсальная газовая постоянная. Это соотношение может быть преобразовано к виду уравнения состояния

p (ρ,T ) =	R	ρT.	(8.6)
	β

Такая взаимосвязь плотности ρ, давления p и температуры T справедлива не только для многих газов, но и для некоторых жидкостей, если давление p не очень велико, а температура T не слишком низкая.

45Менделеев Дмитрий Иванович (27.01.1834–20.01.1907) – русский ученыйэнциклопедист: химик, физикохимик, физик, метролог, экономист, технолог, геолог, метеоролог, нефтяник, педагог, преподаватель, воздухоплаватель, приборостроитель. Открыл периодический закон химических элементов. Профессор Императорского Санкт-Петербургского университета, член-корреспондент Императорской Санкт-Петербургской академии наук.

46Клапейрон Бенуа Поль Эмиль (26.02.1799–28.01.1864) – французский фи-

зик и инженер, автор работ по	термодинамике. Участвовал в проектировании
и строительстве многих железных	дорог и мостов.

9. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ МЕХАНИКИ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА

Вычислительное моделирование напряженно-деформирован- ного состояния элементов и узлов строительных и дорожных машин предполагает корректную математическую постановку (формулировку) краевой задачи, включающую систему дифференциальных уравнений в частных производных, связывающих компоненты тензора напряжения, тензора деформации и вектора перемещения материальных частиц, а также граничные и начальные (для нестационарных уравнений) условия.

В качестве основных уравнений механики деформируемого твердого тела выступают:

– уравнения движения (8.4) (с учетом формулы (7.2)):

d 2u

= ρf

∂σ

∂σxy

∂σ

dt2

∂y

∂z

∂x

d 2u

= ρf

∂σ

dt2

∂z

∂x

∂y

d 2u

= ρf

∂σ

zx +

∂σzy

∂σ

;

dt2

∂y

∂x

∂z

– физические соотношения обобщенного закона Гука (6.4):

σxx =

(1+ ν)(1− 2ν) (1− ν)εxx + νε yy + νεzz

σyy =

(1+ ν)(1− 2ν) νεxx

+ (1− ν)ε yy + νεzz

σzz =

(1+ ν)(1− 2ν) νεxx

+ νε yy + (1− ν)εzz

σxy = σ yx =

εxy , σ yz = σzy

ε yz , σxz = σzx =

εxz ;

+ ν

1+ ν

– кинематические соотношения (5.2)–(5.4):

εxx =

∂u

x ,

ε yy

∂uy

, εzz =

∂u

z ;

∂y

∂x

∂z

∂ux

∂uy

∂ux

∂uz

∂uy

∂uz

εxy =

, ε xz =

ε yz

∂y

∂x

∂z

∂y

∂x

Записанная система пятнадцати дифференциальных уравнений в частных производных содержит пятнадцать искомых функций: шесть независимых компонент σxx, σyy, σzz, σxy, σyz, и σxz тензора напряжения, шесть независимых компонент εxx, εyy, εzz, εxy, εyz, и εxz тензора деформации и три независимые компоненты ux, uy и uz вектора перемещения, то есть число уравнений системы соответствует числу неизвестных.

Подстановка кинематических соотношений (5.2)–(5.4) в формулы обобщенного закона Гука (6.4), а полученных соотношений – в уравнения движения (8.4) позволяет получить три дифференциальных уравнения движения с тремя искомыми функциями перемещения ux, uy и uz, или уравнения Ламе47:

d 2u

= ρfx +

dt2x

2(1+ ν )

∂2u

∂2uy

∂2u

(9.1)

x +

;

∂x∂y

− 2ν

∂x2

∂x∂z

∂x2

∂y2

∂z2

d 2uy

= ρfy +

dt2

2(1+ ν )

47 Ламе Габриель (22.07.1795–01.05.1870) – французский математик, механик, физик и инженер, член-корреспондентПетербургской академии наук, член Парижской академии наук, профессор Политехнической школы и Парижского университета. В1820–1831 гг. работал в Институте корпуса инженеров путей сообщения в Петербурге. Основные труды по математической физике и теории упругости, разработал общую теориюкриволинейныхкоординат. Вчестьнегоназванрядпараметроввтеорииупругости.

∂2u

∂2uy

∂2u

∂2uy

∂y∂x

∂y2

∂x2

∂y2

− 2ν

∂y∂z

d 2u

= ρfz +

dt2z

2(1+ ν )

∂2u

∂2uy

∂2u

∂z∂y

1− 2ν

∂z∂x

∂z2

∂x2

∂y2

+∂2uy ;

∂z2

+∂2uz .

∂z2

9.1. Кинематические граничные условия

Получение единственного решения системы уравнений Ламе (9.1) требует задания кинематических граничных условий, накладываемых на компоненты вектора перемещения. Система (9.1) содержит дифференциальные уравнения в частных производных второго порядка по каждой из пространственных переменных x, y и z. Это означает, что для каждой из искомых функций ux, uy и uz на каждой граничной поверхности необходимо задать кинематические граничные условия (рис. 9.1).

ux = Ux3 uy = Uy3 uz = Uz3

ux = Ux1 uy = Uy1 uz = Uz1

		ux = Ux6
	z	uy = Uy6
	z	uz = Uz6
		uz = Uz6

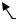ux = Ux5 uy = Uy5 uz = Uz5

ux = Ux2 uy = Uy2 uz = Uz2

ux = Ux4 uy = Uy4 uz = Uz4

Рис. 9.1. Кинематические граничные условия для уравнений Ламе механики деформируемого твердого тела

9.2. Силовые граничные условия

Если математическая модель деформируемого твердого тела содержит полную систему уравнений (5.2)–(5.4), (6.4) и (8.4), получение единственного решения может потребовать задания силовых граничных условий в виде соотношений (формулы) Коши (8.1), накладываемых на компоненты тензора напряжения.

Если, например, поверхность тела перпендикулярна оси x (см. рис. 9.1), проекции вектора нормали nx = 1, ny = 0, nz = 0, и, согласно соотношениям Коши (8.1), компоненты тензора напряжения на этой границе тела принимают значения

σxx = px, σyx = py, σzx = pz.

9.3. Начальные условия

Уравнения движения сплошной среды (8.4) с учетом формулы (7.2) или уравнения Ламе (9.1) содержат вторые производные по времени искомых функций ux, uy и uz. Для получения единственности решения уравнений, содержащих вторую производную по времени, необходимо в каждой точке области, занимаемой рассматриваемым телом, задать два начальных условия для каждой искомой функции в начальный момент времени t = 0:

u				= U 0	,	dux


	x		t =0	x		dt
	x		t =0	x		dt
uy				= U y0 ,		duy


		t=0				dt
		t=0				dt
u				= U 0	,	duz


	z		t =0	z		dt
	z		t =0	z		dt

= v				= V 0 ;
= v				= V 0 ;
t=0	x	t=0		x
	x	t=0		x

= vy			t =0	= Vy0 ;	(9.2)
= vy				= Vy0 ;	(9.2)
t =0
t =0
= v				= V 0 .
= v				= V 0 .
	z	t=0		z
	z	t=0		z

t =0

9.4. Стационарные48 задачи механики деформируемого твердого тела

При изучении стационарного напряженно-деформированного состояния тела производные по времени искомых функций равны нулю. В частности,

d 2u	x	= 0	,	d 2u	y	= 0 ,	d 2u	z	= 0 ,
dt2				dt2			dt2

и система уравнений (5.2)–(5.4), (6.4), (8.4) механики деформируемого твердого тела упрощается:

∂σ

∂σxy

∂σ

+ ρfx = 0

;

∂y

∂x

∂z

∂σyx

∂σyy

∂σyz

+ ρfy = 0

;

∂x

∂y

∂z

∂σ

zx +

∂σzy

∂σ

zz + ρfz = 0

;

∂y

∂x

∂z

σxx = (1+ ν)E(1− 2ν) ((1− ν)εxx + νε yy + νεzz );

σyy = (1+ ν)E(1− 2ν) (νεxx + (1− ν)ε yy + νεzz );

σzz = (1+ ν)E(1− 2ν) (νεxx + νε yy + (1− ν)εzz ) ;

σxy = σ yx =		E	εxy , σ yz = σzy =	E	ε yz , σxz = σzx =	E	εxz ;
	1	+ ν		1+ ν		1+ ν

48 Стационарность напряженно-деформированного состояния изучаемого тела предполагает независимость от времени t коэффициентов дифференциальных уравне-

нийивсехискомыхфункцийσxx, σyy, σzz, σxy, σyz, σxz, εxx, εyy, εzz, εxy, εyz, εxz, ux, uy иuz.

ε xx =

∂u

ε yy

= ∂v

, εzz =

∂w

;

∂x

∂y

∂z

ε xy =

∂u

∂v

εxz =

∂u

∂w

ε yz

∂v

∂w

∂y

∂z

∂x

∂y

Приведенная система пятнадцати дифференциальных уравнений также содержит пятнадцать искомых функций.

Уравнения Ламе (9.1) также упрощаются:

∂2u

∂2uy

∂x∂y

2(1+ ν ) 1

− 2ν

∂x2

∂2u

∂2uy

∂y∂x

∂y2

2(1 + ν ) 1

− 2ν

∂2u

∂2uy

∂z∂y

2(1+ ν ) 1

− 2ν

∂z∂x

+	∂2u	z	+	∂2u	x
		z

	∂x∂z			∂x2

+	∂2u	z	+	∂2uy
		z
				∂x2
	∂y∂z			∂x2

+∂2uz + ∂2uz ∂z2 ∂x2

∂2u

+ ρf

= 0 ;

∂y2

∂z2

∂2u

+ ρf

= 0 ;

∂y2

∂z2

∂2u

+ ρf

= 0 .

∂y2

∂z2

Граничные условия в рассматриваемом случае являются одновременно краевыми, поскольку начальные условия не требуются.

9.5. Краевые условия49 для трехмерной задачи

Для получения единственного решения задачи механики деформируемого твердого тела в общем случае в каждой точке границы тела задаются три граничных условия, при этом возможны различные комбинации кинематических и силовых граничных условий

(см. рис. 9.1):

– три кинематических условия,

ux = Ux, uy = Uy, uz = Uz;

49 Краевыми условиями называется совокупность граничных и начальных условий для задачи, содержащей дифференциальные уравнения с частными производными по времени t и координатам x, y, z.

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке книги