
книги / Строительная механика, динамика и устойчивость композитных конструкций
..pdfЕсли применить к системе процедуру МКЭ, то получим систему линейных соотношений относительно обобщенных узловых перемещений следующего вида:
С 2 |
|
|
В |
|
|
u' |
|
f |
0i |
|
|
||||
|
|
|
|
A |
|
|
|
i |
|
|
|
, |
(1.4.5.6) |
||
|
|
В |
|
|
С 2 |
u'' |
|
0 |
|||||||
|
|
|
|
|
|
|
A |
i |
|
|
|
|
|
|
|
где [B] – глобальная матрица диссипативных коэффициентов. При вычислении амплитуды узловых перемещений доста-
1
точно рассчитать норму (ui 2 ui 2 )2 для определения запаздывания (сдвига по фазе относительно вынуждающей нагрузки)
i arctg |
ui' |
. |
(1.4.5.7) |
|
|||
|
ui'' |
|
|
1.4.6.Анализ неустановившихся процессов
вдиссипативных системах
Если для уравнения движения
A |
2u |
В |
u |
Cu f |
(1.4.6.1) |
||
t |
2 |
t |
|||||
|
|
|
|
||||
применить процедуру МКЭ, то разрешающая система будет иметь вид:
|
A |
|
|
|
В |
|
|
|
С |
|
|
|
F |
|
. |
(1.4.6.2) |
|
u |
|
u |
|
u |
|
|
Интегрирование системы обыкновенных дифференциальных уравнений второго порядка с начальными условиями проводится численно, используя методы Адамса, Рунге – Кутты, Ньюмарка.
1.4.7. Оценка диссипативных характеристик композитных материалов
Композиционные материалы обладают достаточно высокими диссипативными свойствами по сравнению с традиционными металлами и сплавами.
41
Причины: обилие внутренних границ раздела фаз, способность длительное время накапливать повреждения, применение в качестве компонентов композита материалов с высокими вязкоупругими свойствами.
В связи с тем что упругий оператор и диссипативный оператор внутреннего трения подобны, то для оценки эффективных диссипативных характеристик композитов используются методы механики неоднородных сред.
1.5. Стохастические краевые задачи динамики конструкций
Динамическое поведение конструкции описывается операторным уравнением вида:
A |
2u |
В |
u |
Cu f , |
(1.5.1) |
||
t |
2 |
t |
|||||
|
|
|
|
||||
где A, B, C – соответственно инерционный, диссипативный и жесткостный операторы.
Если внешнее воздействие является случайной функцией времени t и координаты r , f (t, r ) , то есть заданы ее статистиче-
ские характеристики (для стационарного эргодического поля это среднее f (t, r ) , дисперсия f (t, r ) и корреляционная
функция k f (r ,t, r ,t ) ), тогда исследование динамического поведения конструкции сводится к отысканию случайного поля u(r,t) ,
удовлетворяющего уравнению (1.5.1) и краевым условиям. Операторная форма уравнения (1.5.1) может иметь следующий вид
L[u] f , |
(1.5.2) |
где L – детерминированный оператор, f (r,t) – случайное поле внешних перегрузок, u(r,t) – случайное, подлежащее определе-
нию поле.
Таким образом, имеем стохастическую краевую задачу динамики.
Рассмотрим основные методы решения задач такого вида.
42

1.5.1. Получение решения в моментных функциях (метод моментных функций)
Применим операцию осреднения к стохастическому дифференциальному уравнению
lim |
|
L[u] f |
1 fk (r,t), |
|
1 L uk (r,t) lim |
||||
|
|
N |
|
N |
|
N |
k 1 |
N |
k 1 |
где uk и fk – реализации случайных полей u и f. Если L( ) – является линейным оператором, то
L[ lim |
1 uk (r,t)] lim |
1 fk (r,t) |
|||
|
|
N |
|
|
N |
N |
N |
k 1 |
|
N |
k 1 |
|
|
L[ u ] f |
, |
||
(1.5.1.1)
(1.5.1.2)
(1.5.1.3)
полученное таким образом сравнение является уже детерминированным уравнением относительно средних значений полей u(r,t)
и f (r,t) .
Подобную процедуру можно выполнить для вариационных функций
|
1 |
N |
|
|
Rf (r ,t ,r ,t) lim |
fk (r ,t ) fk (r ,t) |
(1.5.1.4) |
||
|
||||
N N k 1 |
|
|||
по определению, но, с другой стороны, для реакций fk справедливо операторное уравнение (1.5.1.1), тогда
|
1 |
N |
|
Rf (r ,t , r ,t) lim |
L[uk (r ,t)]L[uk (r ,t )]. |
(1.5.1.5) |
N N k 1
Если L() – линейный оператор, то справедливо представление следующего вида:
|
1 |
N |
|
|
Rf (r ,t, r ,t ) L L lim |
uk (r ,t)uk (r ,t ) |
(1.5.1.6) |
||
|
||||
r ,t r' ,t'' N N k 1 |
|
|||
43
или окончательно
|
|
|
(1.5.1.7) |
Rf (r ,t, r ,t ) L L |
Ru (r ,t, r ,t ) |
||
|
r ,t r' ,t'' |
|
|
детерминированное операторное уравнение относительно ковариационной функции.
Решая полученное уравнение относительно неизвестной функции Ru (r ,t,r ,t ), получим ковариационную функцию иско-
мого поля. Если при этом положить r r и t t , то получим поле дисперсий или флуктуаций случайного поля. Исходная стохастическая задача, таким образом, сводится к решению детерминированных краевых задач, а само решение получается в виде набора детерминированных его моментных функций (от термина «статистический момент»).
1.5.2. Использование функций Грина при построении решения статистической задачи
динамики в моментных функциях
Использование функций Грина при построении решения статистической задачи динамики в моментных функциях. Попробуем разрешить уравнение (1.5.1) относительно u(r ,t) :
u H f . |
(1.5.2.1) |
Для получения оператора Н, необходимо построить функцию Грина, решаявспомогательную краевую задачу дляуравнения вида
L |
G(r ,t,r ,t ) r r (t t ), |
(1.5.2.2) |
r ,t |
|
|
где G(r ,t,r ,t ) – функция Грина. Вспомогательная задача явля-
ется детерминированной и может быть решена обычными методами анализа, тогда уравнение (1.5.1.1) примет вид
u(r ,t) |
t G(r ,t,r ,t ) f r ,t dr dt . |
(1.5.2.3) |
|
V |
|
44
Полученное уравнение справедливо для любых функций f (r ,t ) , в том числе и случайных. Тогда, применяя операторы осреднения к u(r ,t) , можно получить любые интересующие мо-
ментные функции. В прикладных расчетах обычно ограничиваются анализом среднего и дисперсии.
В том случае, когда u(r ,t) и f (r ,t ) являются тензорными случайными полями, решение может быть представлено при помощи тензора Грина Gij (r ,t, r ,t ) в виде
n |
t |
|
u j (r ,t) Gjk (r ,t,r ,t ) fk r ,t dr dt . |
(1.5.2.4) |
|
k 1 V
1.5.3. Метод спектрального разложения
Метод основан на свойствах случайных полей, допускающих каноническое разложение вида:
|
|
f r ,t Fn n r ,t , |
(1.5.3.1) |
n 1
где Fn – случайные величины, n (r ,t) – детерминированные
функции.
В этом случае решение статистической задачи динамики можно разыскивать в подобном виде
|
|
u r ,t Fn n r ,t , |
(1.5.3.2) |
n 1
где Fn – случайные величины, n – некоторые независимые де-
терминированные функции.
Подстановка представлений (1.5.3.2) в исходное уравнение (1.5.2.3) позволяет получить для отыскания n приведением вы-
ражений при одинаковых случайных коэффициентах Fn следующие соотношения
45

L[ n ] n n = 1,2..., |
(1.5.3.3) |
таким образом, статистическая краевая задача сводится к последовательности решения детерминированных задач.
1.5.4. Разложение по собственным формам
Разложение поля u по собственным формам дает представление в виде
|
t n r , |
|
u r ,t Vn |
(1.5.4.1) |
n 1
где n – собственная формаколебаний, un (t) – случайнаяфункция.
Подставляя ряд в уравнение (1.5.2.3) и используя процедуру метода Галеркина и свойство ортогональности собственных форм, получим набор стохастических обыкновенных дифференциальных уравнений
|
d 2u |
n |
2 |
|
du |
n |
2 |
|
F |
(t) |
n = 1,2..., |
(1.5.4.2) |
|
dt2 |
|
|
dt |
u |
|
||||||
|
|
|
n |
n |
n |
n |
|
|
|
|||
где n |
собственные |
частоты, |
|
n коэффициент диссипации, |
||||||||
Fn (t) – случайные функции времени.
Решение каждого из уравнений можно получить, например, используя методы моментных функций.
1.5.5. Численные методы решения статистических задач динамики
Численные методы решения статистических задач динамики в основе своей содержат метод реакций (метод МонтеКарло).
Так, в соответствии с методом реакций
|
|
1 |
N |
1 |
N |
|
|
u r ,t |
lim |
uk (r ,t) |
uk (r ,t) |
(1.5.5.1) |
|||
|
|
||||||
|
N N k 1 |
N k 1 |
|
||||
46
|
|
|
1 |
N |
|
Ru (r ,t, r ,t ) lim |
uk (r ,t)uk (r ,t ) |
|
|||
|
|
||||
|
|
N N k 1 |
(1.5.5.2) |
||
|
1 |
N |
|
|
|
|
|
|
|
||
|
uk (r ,t)uk (r ,t ), |
|
|||
|
|
||||
|
N k 1 |
|
|
|
|
где uk – реализации случайной величины u, определяемые численно, используя для этого процедуру метода конечного элемента
A uk В uk С uk Fk , |
(1.5.5.3) |
где {Fk } – реализация вектора внешних случайных воздействий
на механическую систему.
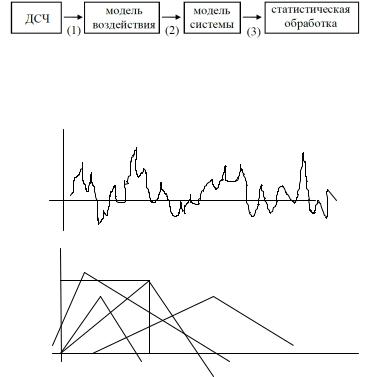
Блок-схема метода Монте-Карло показана на рис. 1.10.
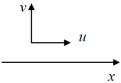
Рис. 1.10. Блок-схема метода Монте-Карло: 1 – методы скользящего суммирования; 2 – метод конечного элемента; 3 – эргодичный процесс по одной реализации (а); и неэргодичный по большому числу разных реализаций (б) (рис. 1.11)
u |
а |
Fа
t0
б
Рис. 1.11. Случайные процессы ( Fa и t0 случайные величины)
47
1.6. Распространение волн в неоднородных средах
Распространение упругих волн в неоднородных средах в общем случае предполагает рассмотрение одного из двух видов:
1.Длина волны значительно больше характерного размера неоднородности.
2.Длину волны нельзя считать существенно большей по сравнению с масштабом неоднородности.
1.6.1. Волны в эквивалентной гомогенной среде
Рассмотрим распространение волн в неоднородной среде при выполнении условия большой длины волны. Приняв данное предположение, можно считать, что неоднородная среда ведет себя как эквивалентная однородная с эффективными упругими и инерционными характеристиками. Тогда основные уравнения динамики примут вид:
ij, j ui,tt , |
|
ij Cijkl kl , |
(1.6.1.1) |
ij (ui, j u j,i )/2,
где – плотность среды, осредненная по объему материала, Cijkl –
эффективные упругие модули среды, рассчитанные с использованием моделей и методов механики композиционных материалов; , и u – осредненные нестационарные поля напряжений, деформаций, перемещений.
|
Подробнее |
рассмотрим одно- |
||||
|
мерный случай: |
|
|
|
||
|
E |
2u |
|
2u |
; |
|
|
x2 |
t |
2 |
|||
|
|
|
; (1.6.1.2) |
|||
|
G |
2v |
|
2v |
||
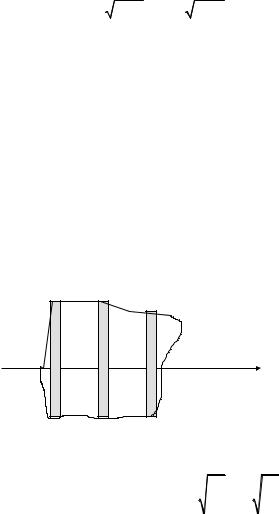
Рис. 1.12. Ориентация |
x2 |
t |
2 |
. |
||
|
|
|
||||
продольной |
Фронт волны распространяется |
|
и сдвиговой волн |
||
с постоянной скоростью, тогда |
||
|
48
u u(x a1t) ; v v(x a2t). |
(1.6.1.3) |
Если ввести обозначение x at (характеристики волнового уравнения) и перейти к новым переменным, то получим:
E |
2u |
a2 |
2u |
; |
G |
2u |
a2 |
2u |
, |
(1.6.1.4) |
|
|
2 |
|
1 |
2 |
|
|
2 |
2 |
2 |
|
|
откуда следуют |
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
E / ; |
a2 |
|
G / |
|
|
(1.6.1.5) |
|||
скорости распространения продольных и сдвиговых волн в материале.
В анизотропных средах скорости волн в направлении главных осей анизотропии отличаются, при этом волны, распространяющиеся в произвольном направлении, образуют продольную и сдвиговую форму деформирования одновременно, их взаимодействие и наложение приводит к сложным динамическим эффектам (рис. 1.12).
1.6.2. Прохождение волн в слоистых средах
Распространение коротких импульсов в неоднородных средах рассмотрим на примере слоистого материала (для простоты двухкомпонентного и периодического). Исследуем скорость распространения волн поперек пакета слоев (рис. 1.13).
1 2 |
1 2 |
х
1 2
1 2
Рис. 1.13. Двухкомпонентная периодическая среда
a |
h1 h2 |
|
h1 |
h2 |
|
; |
a |
|
h1 |
h2 |
|
|
(1.6.2.1) |
||
h1 |
|
|
|
|
|
|
|
||||||||
1 |
t |
|
|
h1 |
1 |
h |
h |
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
2 |
|
||||
|
|
|
(1) |
(2) |
|
|
|
|
|
||||||
|
|
|
|
|
|
E |
|
|
|||||||
|
|
|
a1 |
|
a1 |
|
|
|
1 |
2 |
E |
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
49
Сравним со скоростью распространения длинных волн
|
|
a |
* |
|
|
E* |
; |
|
|
h |
|
|
h |
|
|
|
h |
|
|
, |
|
|
(1.6.2.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|||||||||||
|
|
1 |
|
|
* |
|
|
|
E* |
|
|
E |
|
|
|
E |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
где |
h h h |
; * h1 h2 |
|
; a* |
|
|
|
|
|
|
|
|
|
|
h1 h2 |
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 2 |
h |
|
1 |
h |
2 |
1 |
|
|
|
h1 |
|
|
|
|
|
h2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h1 1 |
h2 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
E |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
Очевидно, что a1 a2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Аналогично можно получить выражение для скорости попе- |
|||||||||||||||||||||||||||
речной волны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a2 |
|
|
|
|
|
|
h1 h2 |
|
|
|
. |
|
|
|
|
|
(1.6.2.3) |
|||||||
|
|
|
|
h |
|
|
1 |
h |
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
G |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
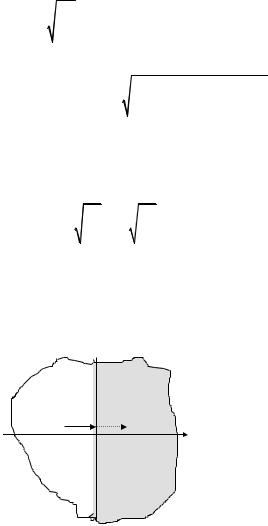
1.6.3. Отражение волн на границах раздела
Путь волны проходит из слоя 1 в слой 2 (рис. 1.14) через поверхность раздела. Запишем условия непрерывности для напряжений при перемещении на границе слоев.
–
 +0
+0
Рис. 1.14. Волны напряжений на границе раздела слоев: σ0 – падающая волна напряжений; σ+ – проходящая волна;
σ– – отраженная волна; |
|
|
|
|
условия на границе раздела фаз |
|
|
u |
|
||
|
u u |
|
|
||
50
