
книги / Методы вычислительной математики
..pdf
|
|
|
|
T ( n ) |
|
|
|
= sup |
|
|
|
T ( n)V |
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
sup |
λmax |
|
|
|
V |
|
|
|
|
= ν. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
V Rm ,V ≠0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V Rm ,V ≠0 |
|
|
|
|
V |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Сравнением последнего неравенства с выражением (2.19) определяется |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точное значение нормы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T (n) |
|
|
|
= ν . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
С учетом этого можно оценить величину погрешности: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z(n) |
|
|
|
|
= |
|
|
|
T (n) z(0) |
|
|
|
|
≤ ν |
|
|
|
z(0) |
|
|
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Построение |
доказательства |
|
|
|
|
|
теоремы 2.5 |
основано на поиске набо- |
|||||||||||||||||||||||||||||||||||||||||||||||||
ра τ(s) , s = |
|
, |
который минимизирует спектральный радиус ν матрицы T (n) . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
1,n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Предполагается, что все собственные значения матрицы А упорядочены: 0 < λ1 = λmin < λ2 <…< λm−1 < λm = λmax .
Известно [9], что если f(A) – матричная функция матричного аргумента А, то f (λ1 ), f (λ2 ), …, f (λm ) – полная система собственных значений матрицы f(A).
Поскольку
T (n) (A)= (E − τ(n) A)(E − τ(n−1) A) … (E − τ(1) A)
является как раз матричной функцией матричного аргумента, то соответствующая скалярная функция
(1 − τ(n)λi )(1 − τ(n−1)λi ) … (1 − τ(1)λi )
определяет собственные значения матрицы T (n) . В этом случае ее спектральный радиус может быть определен как
ν = max (1 − τ(n)λi )(1 − τ(n−1)λi )… (1 − τ(1)λi ).
1≤i≤m
Используя обозначение
f (λ)= (1 − τ(n)λ)(1 − τ(n−1)λ) … (1 − τ(1)λ), |
(2.20) |
||||||||||||||||||||||
спектральный радиус можно определить неравенством ν ≤ |
max |
|
f (λ) |
|
. Тогда |
||||||||||||||||||
|
|
||||||||||||||||||||||
определение набора τ(s) , s = |
|
, сводится к задаче поиска |
λmin ≤λ≤λmax |
|
|
|
|
||||||||||||||||
|
|
|
|||||||||||||||||||||
1,n |
|
|
|
|
|
||||||||||||||||||
min max |
|
f (λ) |
|
= min |
|
|
|
f (λ) |
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
τ(s ) , s= |
1,n |
λmin ≤λ≤λmax |
|
|
|
τ(s ) , s= |
1,n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Функция (2.20) является полиномом степени n, причем f(0) = 1. Иначе говоря, поиск итерационных параметров τ(s) , s =1,n , сводится к задаче об отыскании полинома степени n, наименее уклоняющегося от нуля на отрезке
61

[λmin , λmax ], которая может быть решена с использованием полинома Чебышёва. Корни функции (2.20) принимают значения:
1 − τ(s)λ = 0, λs =1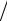 τ(s) , s =1,n
τ(s) , s =1,n
и должны совпадать с корнями полинома Чебышёва
λs = [(λmax + λmin )+ (λmax − λmin )cos((2s −1)π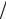 2n)]
2n)]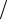 2, s =1,n .
2, s =1,n .
Это означает, что итерационные параметры следует выбирать следующим образом:
(τ(s) )−1 = λs = [(λmax + λmin ) + (λmax − λmin )cos((2s −1)π 2n)] 2 = |
|||
= (λmax + λmin )[1 + (λmax − λmin )t(s) |
(λmax + λmin )] 2= [1 + (1 − ξ)t(s) (1 + ξ)] τ(0) , |
||
τ(s) = τ(0) |
(1 + ρ0t(s) ), s = |
|
. |
1,n |
|||
Использованные обозначения соответствуют введенным ранее при формулировке теоремы. Для оценки нормы погрешности следует заметить, что
ν ≤ max |
|
f (λ) |
|
= |
|
|
|
f |
|
|
|
= 2ρn |
(1 + ρ2n ), |
|
|
|
|
|
|
||||||||
λmin ≤λ≤λmax |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда следует неравенство

 z(n)
z(n) 
 ≤ 2ρ1n
≤ 2ρ1n 
 z(0)
z(0) 

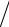 (1 + ρ12n ).
(1 + ρ12n ).
Что и требовалось доказать.
2.4.5. Неявный метод с чебышёвским набором параметров
Рассматривается неявная итерационная схема с положительно определенными матрицами А и В:
B(x(s+1) − x(s) ) τ(s+1) + Ax(s) = f . |
(2.21) |
Эта система уравнений для погрешностей принимает вид |
|
B(z(s+1) − z(s) ) τ(s+1) + Az(s) = 0. |
|
Указанные свойства матрицы В позволяют представить |
ее в виде |
B = B1 2 B1 2 и записать систему уравнений в форме |
|
(B1 2 z(s+1) − B1 2 z(s) ) τ(s+1) + B−1 2 Az(s) = 0. |
|
Обозначение B1 2 z(s) = v(s) , z(s) = B−1 2v(s) используется для преобразования
последней системы уравнений к виду
(v(s+1) − v(s) )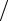 τ(s+1) + Cv(s) = 0 ,
τ(s+1) + Cv(s) = 0 ,
где C = B−1 2 AB−1 2 – симметричная положительно определенная матрица, причем минимальное (максимальное) собственное значение матрицы B−1 A является одновременно и минимальным (максимальным) собственным значением для матрицы С.
62

Теорема 2.6. Пусть А и В – симметричные положительно определенные матрицы, λmin , λmax – наименьшее и наибольшее собственные значения матри-
цы B−1 A. Для заданного числа n итераций неявный чебышёвский метод (2.21) имеет минимальную погрешность при наборе τ(s) , s =1,n , определенном условиями предыдущей теоремы, где ξ = λmin 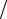 λmax .
λmax .
Удачным выбором матрицы В можно приблизить значение параметра ξ к 1, что приведет к понижению погрешности 
 z(n)
z(n) 
 .
.
2.4.6. Метод минимальных невязок
Погрешность z(s) = x(s) − x решения системы линейных алгебраических уравнений вида1 Ax = f определить невозможно, поскольку точное решение x
неизвестно. Однако можно оценить невязку
r(s) = Az(s) = A(x(s) − x)= Ax(s) − Ax = Ax(s) − f ,
показывающую, насколько полученное численное решение не удовлетворяет исходному уравнению. Рассматривается явный итерационный метод:
(x(s+1) − x(s) )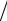 τ(s+1) + Ax(s) = f .
τ(s+1) + Ax(s) = f .
Из приведенного соотношения определяется величина x
x(s+1) = x(s) − τ(s+1) (Ax(s ) − f )= x(s) − τ(s+1)r(s ).
При использовании этой итерационной схемы для s + 1 шага следует так подобрать итерационный параметр τ(s+1) , чтобы при известном x(s) значение невязки r стало наименьшим. Для этого с использованием найденного x(s) оценивается невязка для шага s + 1:
r(s+1) = Ax(s+1) − f = Ax(s) − τ(s+1) Ar(s) − f = r(s) − τ(s+1) Ar(s) .
Как и ранее, вычисляется квадрат нормы невязки:

 r(s+1)
r(s+1) 
 2 = (r(s) − τ(s+1) Ar(s) , r(s) − τ(s+1) Ar(s) )=
2 = (r(s) − τ(s+1) Ar(s) , r(s) − τ(s+1) Ar(s) )=
= (r(s) , r(s) )− (τ(s+1) Ar(s) , r(s) )− (r(s) , τ(s+1) Ar(s) )+ (τ(s+1) Ar(s) , τ(s+1) Ar(s) )=
= 
 r(s)
r(s) 
 2 − 2τ(s+1) (r(s) , Ar(s) )+ (τ(s+1) )2
2 − 2τ(s+1) (r(s) , Ar(s) )+ (τ(s+1) )2 
 Ar(s)
Ar(s) 
 2 .
2 .
При выводе последнего выражения учтено, что
(Au, v)= (u, AT v)= (u, Av),
1 Здесьидалеепредполагается, чтоА– симметричнаяположительноопределеннаяматрица.
63

AT = A – в силу симметрии матрицы. Полученное соотношение между невязками на соседних шагах итерационной процедуры можно рассматривать как функциональную зависимость r(s+1) (τ(s+1) ). Для нахождения итерационного па-
раметраτ(s+1) , при котором невязка r(s+1) минимальна, используется теорема Ферма1:
d 
 r(s+1)
r(s+1) 
 2
2 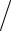 dτ(s+1) = −2(r(s) , Ar(s) )+ 2τ(s+1)
dτ(s+1) = −2(r(s) , Ar(s) )+ 2τ(s+1) 
 Ar(s)
Ar(s) 
 2 = 0 ,
2 = 0 ,
τ(s+1) = (r(s) , Ar(s) )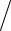

 Ar(s)
Ar(s) 
 2 .
2 .
Оценка невязки получаемого решения:

 A(x(s) − x)
A(x(s) − x)
 ≤ ρ0s
≤ ρ0s 
 A(x(0) − x)
A(x(0) − x)
 .
.
Здесь ρ0 = (1 − ξ)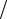 (1 + ξ); ξ = λmin
(1 + ξ); ξ = λmin 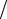 λmax ; λmin , λmax – наименьшее и наибольшее собственные значения матрицы А; s – номер итерации.
λmax ; λmin , λmax – наименьшее и наибольшее собственные значения матрицы А; s – номер итерации.
2.4.7. Метод минимальных поправок
Неявная итерационная схема
B(x(s+1) − x(s) )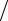 τ(s+1) + Ax(s) = f
τ(s+1) + Ax(s) = f
представляется в виде
B(x(s+1) − x(s) )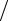 τ(s+1) + r(s) = 0 ,
τ(s+1) + r(s) = 0 ,
x(s+1) = x(s) − τ(s+1) B−1r(s) ,
где, как и ранее, r(s) = Ax(s) − f . Вектор w(s) = B−1r(s) называется поправкой. Очевидно, что поправка w(s) удовлетворяет уравнению
B(w(s+1) − w(s) )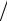 τ(s+1) + Aw(s) = 0 .
τ(s+1) + Aw(s) = 0 .
Предполагая, что В – симметричная положительно определенная матрица, можно с ее использованием определить норму в виде

 v
v
 B =
B = 
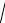 (Bv,v).
(Bv,v).
1 Пьер Ферма [17.8.1601 – 12.1.1665] – французский математик. По профессии был юристом, с 1631 года являлся советником парламента в Тулузе. Основные научные труды изданы лишь после его смерти.
Теорема Ферма [10]: пусть функция y = f(x), непрерывная в некотором замкнутом интервале [a, b], принимает свое наименьшее (наибольшее) значение во внутренней точке ξ этого интервала. Если в точке ξ производная функции f(x) существует, то она равна нулю.
64

Квадрат нормы поправки w(s+1) = w(s) − τ(s+1) B−1 Aw(s) определяется выражением

 w(s+1)
w(s+1) 
 2B = (B(w(s) − τ(s+1) B−1 Aw(s) ), w(s) − τ(s+1) B−1 Aw(s) )=
2B = (B(w(s) − τ(s+1) B−1 Aw(s) ), w(s) − τ(s+1) B−1 Aw(s) )=
=(Bw(s) , w(s) )−τ(s+1) (Aw(s) , w(s) )−τ(s+1) (Bw(s) , B−1 Aw(s) )+(τ(s+1) )2 (Aw(s) , B−1 Aw(s) )=
=(Bw(s) , w(s) )− 2τ(s+1) (Aw(s) , w(s) )− (τ(s+1) )2 (Aw(s) , B−1 Aw(s) )=
= |
|
|
|
|
w(s) |
|
|
|
2 |
|
|
|
|
− 2τ(s+1) |
|
|
|
w(s) |
|
|
|
2 |
|
|
|
|
− (τ(s+1) )2 |
|
|
|
|
|
|
|
Aw(s) |
|
|
|
|
|
2 |
. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B−1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Для получения этого выражения использовались соотношения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Bw(s ), B−1 Aw(s ) )= ((B−1 A)T Bw(s), w(s ) )= (AB−1Bw(s), w(s ) )= (Aw(s ), w(s) ), |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
AT = A, |
|
(B−1 )T = B−1 , |
|
w(s) |
|
|
|
2 = (Aw(s) , w(s) ), |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aw(s) |
|
|
|
2 |
|
|
|
|
= (Aw(s) , B−1 Aw(s) ). |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
w(s+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Норма поправки |
|
|
|
|
будет минимальной при условии |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
d |
|
|
|
w(s+1) |
|
|
|
2 dτ(s+1) = −2 |
|
|
|
w(s) |
|
|
|
2 + 2τ(s+1) |
|
|
|
Aw(s) |
|
|
|
2 |
= 0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B−1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Решением этого уравнения является значение итерационного параметра |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
τ(s+1) = |
|
|
|
w(s) |
|
|
|
2 |
|
|
|
|
Aw(s) |
|
|
|
2 |
|
|
|
|
= (Aw(s) , w(s) ) (Aw(s) , B−1 Aw(s) ). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
B−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Для реализации метода минимальных поправок требуется на каждой итерации |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
решать систему уравнений |
|
|
Bw(s) = r(s) , что позволяет вычислять поправку w(s) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Кроме этого необходимо определять |
|
|
|
решение |
|
системы уравнений Bv(s) = Aw(s) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ивычислять v(s) = B−1 Aw(s) , |
|
|
|
|
требующееся |
|
для |
|
нахождения |
очередного значения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
итерационного параметра. Погрешность метода минимальных поправокоценивается следующимобразом(сучетомвведенногоопределениянормы):
|
A(x(s) − x) |
|
|
|
B |
−1 |
≤ ρ0s |
|
|
|
A(x(0) − x) |
|
|
|
B |
−1 . |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Как и ранее, ρ0 = (1 − ξ) (1 + ξ); |
ξ = λmin |
λmax ; |
|
λmin , λmax – наименьшее |
|||||||||||||
и наибольшее собственные значения матрицы |
B−1 A; s – номер итерации. |
||||||||||||||||
2.4.8. Метод скорейшего спуска |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Относительно погрешности z(s) |
= x(s) − x |
итерационная схема Ричардсона, |
|||||||||||||||
как показано ранее, принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(z(s+1) − z(s) )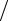 τ(s+1) + Az(s) = 0 .
τ(s+1) + Az(s) = 0 .
65

Определяется величина погрешности z(s+1) :
z(s+1) = z(s) − τ(s+1) Az(s) .
Квадрат нормы z(s+1) определяется с учетом свойств матрицы А:

 z(s+1)
z(s+1) 
 2A = (Az(s+1) , z(s+1) )= (A(z(s) − τ(s+1) Az(s) ), z(s) − τ(s+1) Az(s) )=
2A = (Az(s+1) , z(s+1) )= (A(z(s) − τ(s+1) Az(s) ), z(s) − τ(s+1) Az(s) )=
=(Az(s) , z(s) )− (Aτ(s+1) Az(s) , z(s) )− (Az(s) , τ(s+1) Az(s) )+ (Aτ(s+1) Az(s) , τ(s+1) Az(s) )=
=(Az(s) , z(s) )− 2τ(s+1) (Az(s) , Az(s) )+ (τ(s+1) )2 (A2 z(s) , Az(s) )=
= 
 z(s)
z(s) 
 2A − 2τ(s+1)
2A − 2τ(s+1) 
 Az(s)
Az(s) 
 2 + (τ(s+1) )2
2 + (τ(s+1) )2 
 Az(s)
Az(s) 
 2A .
2A .
При выводе последнего соотношения учтено, что при A = AT
(AAz(s) , z(s) )= (Az(s) , Az(s) ).
Полученное выражение может рассматриваться как квадратичная функция итерационного параметра τ(s+1) . Для нахождения значения итерационного параметра, доставляющего экстремум этому выражению, используется теорема Ферма:
d |
|
|
|
z(s+1) |
|
|
|
2 |
|
|
|
|
|
dτ(s+1) |
= −2 |
|
|
|
Az(s) |
|
|
|
2 + 2τ(s+1) |
|
|
|
Az(s) |
|
|
|
2 |
= 0, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
τ(s+1) = |
|
|
|
Az(s) |
|
|
|
2 |
|
|
|
Az(s) |
|
|
|
2 |
|
|
|
= (Az(s) , Az(s) ) (A2 z(s) , Az(s) ). |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вторая производная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d(τ(s+1) )2 = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
d |
2 |
|
|
|
z(s+1) |
|
|
|
2 |
|
|
|
Az(s) |
|
|
|
2 > 0 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
положительна в силу положительной определенности А, то есть выражение

 z(s+1)
z(s+1) 
 2A = (Az(s+1) , z(s+1) ) принимает наименьшее значение при найденном τ(s+1) .
2A = (Az(s+1) , z(s+1) ) принимает наименьшее значение при найденном τ(s+1) .
Учитывая, что Az(s) = r(s) – невязка решения системы уравнений, можно определить искомый итерационный параметр
τ(s+1) = 
 r(s)
r(s) 
 2
2 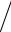

 r(s)
r(s) 
 2A .
2A .
Погрешность решения системы линейных алгебраических уравнений методом скорейшего спуска оценивается выражением
|
x(s) − x |
|
|
|
|
≤ ρ0s |
x(0) − x |
, |
|
|
|
|
|
A |
|
|
A |
|
|
|
|
|
||||
где ρ0 = (1 − ξ) (1 + ξ); ξ = λmin λmax ; |
λmin , λmax |
– наименьшее и наибольшее |
||||||
собственные значения матрицы А; s – номер итерации.
66

2.4.9. Неявный метод скорейшего спуска
Рассматривается неявная итерационная схема вида
B(x(s+1) − x(s) )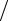 τ(s+1) + Ax(s) = f
τ(s+1) + Ax(s) = f
с симметричной и положительно определенной матрицей B. Для погрешности z(s) = x(s) − x эта схема принимает вид
B(z(s+1) − z(s) )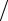 τ(s+1) + Az(s) = 0.
τ(s+1) + Az(s) = 0.
Отсюда получается, что z(s+1) = z(s) − τ(s+1) B−1 Az(s) симметрии матрицы А, определяется выражение

 z(s+1)
z(s+1) 
 2A = (Az(s+1) , z(s+1) )=
2A = (Az(s+1) , z(s+1) )=
= (Az(s) , z(s) )− 2τ(s+1) (Az(s) , B−1 Az(s) )+ (τ(s+1) )2 (AB
. Как и ранее, с учетом
−1 Az(s) , B−1 Az(s) )=
= |
|
|
|
z(s) |
|
|
|
2 |
− 2τ(s+1) |
|
|
|
Az(s) |
|
|
|
2 |
+ (τ(s+1) )2 |
|
|
|
B−1 Az(s) |
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
B−1 |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Благодаря положительной определенности матрицы А,
(Az(s+1) , z(s+1) )> 0 ,
минимум полученного выражения достигается при значении итерационного параметра
τ(s+1) = |
|
|
|
Az(s) |
|
|
|
2 |
|
|
|
B−1 Az(s) |
|
|
|
2 |
= |
|
|
|
r(s) |
|
|
|
2 |
|
|
|
B−1r(s) |
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
B−1 |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
B−1 |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Погрешность неявного метода скорейшего спуска оценивается неравенством

 x(s) − x
x(s) − x
 A ≤ ρ0s
A ≤ ρ0s 
 x(0) − x
x(0) − x
 A ,
A ,
где ρ0 = (1 − ξ)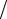 (1 + ξ); ξ = λmin
(1 + ξ); ξ = λmin 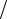 λmax ; λmin , λmax – наименьшее и наибольшее собственные значения матрицы B−1 A; s – номер итерации.
λmax ; λmin , λmax – наименьшее и наибольшее собственные значения матрицы B−1 A; s – номер итерации.
2.4.10. Скорость сходимости
Ранее утверждалось, что если итерационный метод в некотором смысле сходится, то он сходится к решению исходной задачи (2.1). Быстрота достижения результата существенно зависит от того, насколько удачно («близко» к решению) выбрано начальное приближение. В общем случае условия сходимости итерационного метода решения системы линейных алгебраических уравнений определяются следующей теоремой, доказательство которой можно найти, например, в книге [35].
Теорема 2.7. Итерационный метод
B(x(s+1) − x(s) )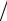 τ + Ax(s) = f , s = 0,1, 2, …
τ + Ax(s) = f , s = 0,1, 2, …
67
сходится при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы (E − τB−1 A) по модулю меньше единицы.
При практическом использовании итерационных методов важен не только сам факт сходимости последовательности получаемых решений, но и скорость, с которой эта последовательность сходится к точному результату. Если для погрешности используемого метода имеет место оценка вида

 x(s) − x
x(s) − x
 ≤ qs
≤ qs 
 x(0) − x
x(0) − x
 , s = 0,1, 2, …,
, s = 0,1, 2, …,
то говорят, что итерационный метод сходится со скоростью геометрической прогрессии со знаменателем q. Эта оценка показывает, во сколько раз уменьшается начальная погрешность после проведения заданного числа итераций.
Пусть задано произвольное целое число k > 0 и требуется, чтобы после выполнения n итераций начальная погрешность уменьшилась не менее, чем в k раз, то есть 
 x(n) − x
x(n) − x
 ≤
≤ 
 x(0) − x
x(0) − x

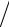 k . Это имеет место в случае qn ≤ k −1 , откуда
k . Это имеет место в случае qn ≤ k −1 , откуда
получается
n ≥ ln(k )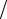 ln(1
ln(1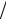 q).
q).
Целая часть этой дроби будет минимальным числом итераций, необходимым для достижения заданной точности. Выражение ln(1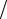 q) называется скоростью сходимости итерационного метода. Эта скорость целиком определяется свойствами матрицы перехода (E − τB−1 A) и не зависит от номера итерации, выбора начального приближения и задаваемой точности. Чем выше скорость сходимости, тем выше производительность выбранного метода решения системы линейных алгебраических уравнений.
q) называется скоростью сходимости итерационного метода. Эта скорость целиком определяется свойствами матрицы перехода (E − τB−1 A) и не зависит от номера итерации, выбора начального приближения и задаваемой точности. Чем выше скорость сходимости, тем выше производительность выбранного метода решения системы линейных алгебраических уравнений.
Контрольные вопросы и задания
2.1.Какие методы решения системы линейных алгебраических уравнений называются прямыми и итерационными?
2.2.Сформулируйте условия существования и единственности решения системы линейных алгебраических уравнений.
2.3.Сформулируйте условия разрешимости системы линейных алгебраических уравнений методом Гаусса.
2.4.Покажите, какую структуру будут иметь матрицы, равные произведениям A−1B, AB−1 , если А и В являются обратимыми верхними (нижними) тре-
угольными матрицами.
68
2.5.Как можно вычислить определитель матрицы коэффициентов, используя процедуру метода Гаусса?
2.6.Обоснуйте возможность построения обратной матрицы с помощью ка- кого-либо численного метода решения системы линейных алгебраических уравнений.
2.7.Выбор «главного» элемента при использовании метода Гаусса возможен с помощью перестановки либо строк, либо столбцов. Обоснуйте, какой вариант предпочтителен.
2.8.Сформулируйте условия применимости метода «квадратного корня» для решения системы линейных алгебраических уравнений.
2.9.Сравните методы Гаусса и квадратного корня для решения системы линейных алгебраических уравнений. Укажите достоинства и недостатки каждого из этих методов.
2.10.Сформулируйте понятие устойчивости системы линейных алгебраических уравнений.
2.11.Чему равно и что характеризует число обусловленности системы линейных алгебраических уравнений?
2.12.Определите смысл условия 
 δA
δA
 <
< 
 A−1
A−1 
 −1 теоремы 2.1 .
−1 теоремы 2.1 .
2.13.Какую погрешность: относительную 
 δx
δx

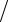

 x
x
 или абсолютную
или абсолютную 
 δx
δx
 – целесообразно оценивать при выполнении вычислений на ЭВМ?
– целесообразно оценивать при выполнении вычислений на ЭВМ?
2.14.Приведите классификацию итерационных методов решения системы линейных алгебраических уравнений. Какие критерии можно использовать для остановки итерационного процесса?
2.15.Укажите геометрический смысл сходимости (расходимости) решения системы алгебраических уравнений при использовании итерационных методов.
2.16.Дайте определение понятия скорости сходимости итерационного
процесса.
2.17.Обоснуйте идею и поясните условия применимости метода Якоби.
2.18.Обоснуйте идею и поясните условия применимости метода Зейделя.
2.19.Покажите, что из условия B – τA/2 > 0 теоремы 2.4 следует существование обратной матрицы B–1.
2.20.Докажите справедливость неравенства (Dx, x) > 0, использованного при доказательстве следствия 1 из теоремы 2.4.
2.21.Укажите условия применимости метода верхней релаксации.
69
2.22.Сформулируйте условия сходимости стационарного итерационного
метода.
2.23.Сформулируйте задачу, решение которой приводит к построению полинома Чебышёва на отрезках [–1, 1] и [a, b].
2.24.В чем преимущество метода решения системы линейных алгебраических уравнений с чебышёвским набором параметров?
2.25.Опишите порядок выбора итерационных параметров в методе минимальных невязок.
2.26.Опишите порядок выбора итерационных параметров в методе минимальных поправок.
2.27.Опишите порядок выбора итерационных параметров в явном методе скорейшего спуска.
2.28.Опишите порядок выбора итерационных параметров в неявном методе скорейшего спуска.
70
