книги / Математика. Функции нескольких переменных

dz

f x, y

x

f x, y

y .

x

y

Найдем

z

и z :

x

y

z

2x y ,

z x 2 y .

x

y

z

6 2 8 ,

z

3 4 7 .

x

y

M x, y, z из положе-

u

x2 y2 z2 при перемещении точки

ния M1 10;10;5 в положение M2 9;11;6 .

du

u x u

y u

z .

x

y

z

u

1

2x

x

;

x

2 x2 y2 z2

x2 y2 z2

u

1

2 y

y

;

y

2 x2 y2 z2

x2

y2 z2

u

1

2z

z

.

z

2 x2 y2 z2

x2

y2 z2

Вычислим частные производные в точке M1 10;10;5 :

u

10

10

2

;

x

M

1

100

100 25

15

3

u

10

10

2

;

y

M

1

100

100 25

15

3

u

5

5

1

.

z

M

1

100

100 25

15

3

Будем полагать, что 1,01 3 1,98 3

есть частное значение

функции z f x, y

в точке M 1,01;1,98 .

x3 y3

На основании формулы (5.18)

f x x, y y

f x, y

f x, y

x

f x, y

y ,

y

x

Найдем

z

и

z

в точке 1; 2 :

x

y

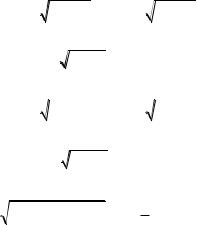
z

1

3x2

3x2

x

;

2 x3

y3

2 x3 y3

z

3 12

3

1

.

x

2

1;2

2

13 23

3

2

z

1

3y2

3y2

y

;

2 x3

y3

2 x3 y3

z

3 22

12

2 .

y

6

13

23

1;2

2

Основные формулы и рисунки

Определения и замечания

1.

z f x, y

(6.1)

Если z f x, y

есть

диф-

x x t , y y t ,

(6.2)

ференцируемая

функция

двух

z f x t , y t

(6.3)

переменных x

и

y,

которые

в

свою очередь, являются диффе-

ренцируемыми функциями неза-

висимой переменной t (6.2), то

сложная функция (6.3) есть диф-

ференцируемая

функция одной

переменной t.

2.

dz

z

dx

z

dy

(6.4)

dz

– полная производная функ-

y

dt

x

dt

dt

dt

ции z по t.

Следует запомнить:

z

z

x ,

y

– частные производные,

так

как

функция

z f x, y

–

функция двух переменных, а

dx

,

dt

dy

– обычные производные, т.к.

dt

x и y – функции одной перемен-

ной t.

Замечание

В формуле (6.4) два слагае-

мых,

так

как

функция

z f x, y – функция двух пере-

менных.

Основные формулы и рисунки

Определения и замечания

3.

Если z f x1, x2 ,..., xn

– диффе-

ренцируемая

функция

перемен-

ных x1, x2 ,..., xn

(6.5),

которые в

z f x1, x2 ,..., xn ,

(6.5),

свою очередь

являются диффе-

ренцируемыми функциями неза-

x1 x1 t ,

висимой переменной t (6.6), то

x2 x2 t ,

сложная функция (6.7) есть диф-

ференцируемая

функция

одной

………...

(6.6)

переменной t.

xn

xn t ,

z f x

t , x t ,..., x

t

(6.7)

1

2

n

4.

dz

z

dx1

z

dx2

...

dz

– полная производная функ-

dt

x

dt

x

dt

dt

1

2

(6.8)

z

dxn

ции z по t.

x

dt

Замечание

n

Формулы (6.4) и (6.8) явля-

ются обобщением правила диф-

ференцирования

сложной

функ-

ции одной переменной.

5.

z f x, y ,

y y x

(6.9)

Если z f x, y

есть дифферен-

z f x, y

x

(6.10)

цируемая функция двух

пере-

менных, причем x – независимая

переменная,

а

y y x

есть

дифференцируемая функция по x

(6.9), то сложная функция (6.10)

есть дифференцируемая функция

одной переменной x.

6.

dz

z

z

dy

(6.11)

dz

– полная производная функ-

dx

x

y

dx

dx

ции z по x.

Основные формулы и рисунки

Определения и замечания

Замечание

В

правой части

равенства

(6.11) мы находим частную про-

изводную

z

, так как z – функ-

x

ция двух переменных x и y.

В

левой

части производная

dz

есть

производная

сложной

dx

функции

одной

переменной

x

(6.10).

7.

z f x, y ,

Если

z f x, y

есть

диф-

x x u,v ,

(6.12)

ференцируемая

функция

двух

y y u,v ,

переменных

x и

y, которые,

в

свою очередь, являются диффе-

z f x u,v , y u,v

(6.13)

ренцируемыми функциями по u и

v (6.12), то сложная функция

(6.13)

есть

дифференцируемая

функция двух переменных u и v.

z

z

x

z

y

Следует запомнить:

8.

x

y

u

(6.14)

частная

производная

сложной

u

u

z

z

x

z

y

функции (6.13) равна сумме про-

изведений частных производных

v x v y v

(6.15)

по

промежуточным аргументам

(x и y) на частные производные

этих аргументов (x и y) по соот-

ветствующей независимой пере-

менной (u или v) (6.14, 6.15).

Замечание

Правило

дифференцирова-

ния сложной функции (6.13) ос-

тается справедливым для функ-

ции с любым количеством про-

межуточных аргументов, кото-

рые

зависят

от

любого

числа

Основные формулы и рисунки

Определения и замечания

независимых переменных.

z f x , x ,..., x

,

(6.16)

z

–

функция

аргументов

1

2

n

x1, x2 ,..., xn (6.16),

которые явля-

x1 x1 u1,u2 ,...,un ,

ются функциями

независимых

x2 x2 u1,u2 ,...,un ,

(6.17)

переменных u ,u ,...,u (6.17).

1 2

n

……………………

xn xn u1,u2 ,...,un

z

z

x1

z

x2

x

x

u

u

u

1

1

1

2

1

...

z

xn

x

u

n

1

z

z

x1

x

u

2

u

2

1

z

x2

...

z

xn

x

u

2

x

u

2

2

n

………………………….…(6.18)

z

z

x1

x

u

n

u

n

1