
книги / Тестовые задания по курсу высшей математики. Ч. 1 Линейная алгебра. Векторная алгебра. Аналитическая геометрия
.pdf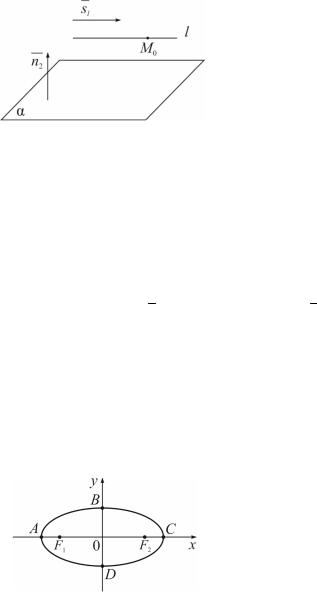
Решение
|
|
|
|
Рис. 3.8 |
|
|||
Прямая |
x − x0 |
= |
y − y0 |
= |
z − z0 |
|
проходит через точку |
|
m |
n |
p |
||||||
|
|
|
|
|||||
M0 (x0 , y0 , z0 ) , параллельно вектору s = {m;n; p} . Плоскость задана уравнением Ax + By + Cz + D = 0 , где n = { A; B;C} – нормальный
вектор плоскости (рис. 3.8).
Первое условие Am + Bn + Cp = 0 представляет собой равенство
нулю скалярного произведения векторов n и s . Поэтому векторы n и s перпендикулярны.
Второе условие означает, что точка M0 не принадлежит плос-
кости. Отсюда следует, что прямая и плоскость параллельны.
Верный ответ № 1.
Вопрос 3.1.19
Число вершин эллипса равно … .
Решение
Рис. 3.9
61
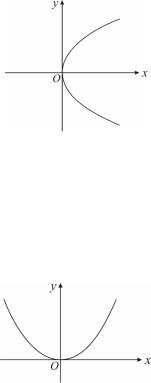
Рассмотрим эллипс, изображенный на рис. 3.9. Для него оси координат являются осями симметрии. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Для данного эллипса точки A, B,C, D – его вершины.
Ответ: 4.
Вопрос 3.1.20
Число осей симметрии параболы равно … .
Решение
Рис. 3.10
Рассмотрим параболу, изображенную на рис. 3.10. Она имеет каноническое уравнение y2 = 2 px( p > 0) . Переменная y входит
в уравнение в четной степени, значит, парабола симметрична относительно оси Ox . Ось Oy не является осью симметрии, так как пе-
ременная x входит в уравнение в первой степени.
Рис. 3.11
Рассмотрим параболу, изображенную на рис. 3.11. Она имеет каноническое уравнение x2 = 2 py( p > 0) . Переменная x входит
62
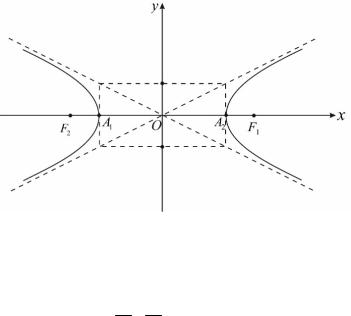
в уравнение в четной степени, значит, парабола симметрична относительно оси Oy . Ось Ox не является осью симметрии, так как пе-
ременная y входит в уравнение в первой степени. Следовательно, у параболы одна ось симметрии.
Ответ: 1.
Вопрос 3.1.21
Ось симметрии, пересекаемая гиперболой, называется ... осью гиперболы.
Рис. 3.12
Решение
Рассмотрим гиперболу, изображенную на рис. 3.12. Она имеет
каноническое уравнение x2 − y2 = 1 . a2 b2
Оси координат являются осями симметрии данной гиперболы. С осью Oy данная гипербола не пересекается, а с осью Ox имеет
две точки пересечения. Ось симметрии, которую гипербола пересекает, называют действительной осью симметрии, а точки пересечения с ней называются вершинами гиперболы.
63
Вопрос 3.1.22
Центрально симметричными кривыми второго порядка являются… .
1)эллипс,
2)гипербола,
3)парабола,
4)окружность.
Решение
Заметим, что любое уравнение кривой второго порядка путем
преобразования параллельного переноса или поворота осей может
быть преобразовано в каноническое уравнение эллипса |
|
x2 |
+ |
y2 |
= 1 , |
|||||||||||||||
|
a2 |
b2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
гиперболы |
x2 |
− |
y2 |
= 1, параболы |
y2 |
= 2 px |
или |
окружности |
||||||||||||
a2 |
b2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 + y2 = R2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Канонические |
уравнения эллипса |
|
x2 |
+ |
y2 |
= 1 , |
|
гиперболы |
||||||||||
|
|
|
a2 |
b2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x2 |
− |
y2 |
= 1 и окружности x2 + y2 = R2 |
содержат переменные x и y |
|||||||||||||||
|
a2 |
|
||||||||||||||||||
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
только в четных степенях, следовательно, эллипс, гипербола, окружность симметричны относительно осей Ox и Oy , а также
относительно точки O(0;0) , которая является центром указанных
кривых.
Эллипс, гипербола, окружность – центрально симметричные кривые второго порядка.
Парабола к центрально симметричным кривым не относится, так как имеет только одну ось симметрии и не имеет центра симметрии.
Верные ответы № 1, № 2, № 4.
64
Вопрос 3.1.23
Если эллипс задан уравнением |
x2 |
+ |
y2 |
= 1 и a > b , то … |
|
a2 |
b2 |
||||
|
|
|
1)фокусы расположены в точках (a;0) и(−a;0) ;
2)фокусы расположены в точках (0;b) и(0;−b) ;
3)фокусы расположены на оси Ox ;
4)фокусы расположены на оси Oy .
Решение
Фокусы любого эллипса расположены на большей оси симметрии эллипса.
Если эллипс задан уравнением |
x2 |
+ |
y2 |
= 1 и a > b , то большая |
|
a2 |
b2 |
||||
|
|
|
ось симметрии принадлежит оси Ox и фокусы расположены на оси Ox .
Верный ответ № 3.
Вопрос 3.1.24
Если эллипс задан уравнением |
x2 |
+ |
y2 |
= 1 , то … |
|
a2 |
b2 |
||||
|
|
|
1)точка (0;0) является центром симметрии эллипса;
2)прямая x = 0 является осью симметрии эллипса;
3)прямые x = a иx = −a являются осями симметрии эллипса;
4)прямые y = ± ba x являются асимптотами эллипса.
Решение
Если эллипс задан каноническим уравнением |
x2 |
+ |
y2 |
= 1 , то |
|
a2 |
b2 |
||||
|
|
|
оси координат x = 0 и y = 0 являются двумя взаимно перпендику-
лярными осями симметрии эллипса.
Начало координат является центром симметрии. Асимптот у эллипса нет. Поэтому верные высказывания № 1, 2.
65
Вопрос 3.1.25
Действительная ось симметрии гиперболы |
x2 |
− |
y2 |
= 1 имеет |
||
a2 |
b2 |
|||||
уравнение… |
|
|
||||
|
|
|
|
|||
1) |
x = 0, |
|
|
|
|
|
2) |
y = 0, |
|
|
|
|
|
3) |
x = a, |
|
|
|
|
|
4) |
y = b. |
|
|
|
|
|
Решение
Поскольку данное уравнение является каноническим уравнением гиперболы, то оси координат являются осями симметрии гиперболы. Найдем точки пересечения гиперболы с осями координат. По-
ложим y = 0 , тогда получим уравнение |
x2 |
= 1, которое имеет два |
|||
a2 |
|||||
|
|
|
|
||
решения x = ±a . А при x = 0 получим уравнение − |
y2 |
= 1, которое |
|||
b2 |
|||||
|
|
|
|
||
решений не имеет. Таким образом, данная гипербола ось Ox пересекает, а ось Oy – нет. Следовательно, действительная ось гипербо-
лы имеет уравнение y = 0 .
Верный ответ № 2.
§3.2. Задачи
Задача № 3.2.1
Уравнение прямой, проходящей через точки A(1;−1)
иB(11;−6) , имеет вид…
1)x − 2 y − 3 = 0,
2)x + 8y + 7 = 0,
3)2x + y − 16 = 0,
4)x + 2 y + 1 = 0.
66

Решение
Уравнение прямой, проходящей через две данные точки
M1 (x1; y1 ) и M2 (x2 ; y2 ), имеет вид |
x − x1 |
= |
|
||
|
x2 − x1 |
|
кущие координаты прямой. Составим уравнение прямой AB :
x − 1 = y − ((−1)) ; 11 − 1 −6 − −1
x − 1 |
= |
y + 1 |
; |
|
10 |
|
−5 |
||
|
|
|
||
x − 1 |
= |
y + 1 |
; |
|
2 |
|
−1 |
||
|
|
|
||
− x + 1 = 2y + 2;
x + 2 y + 1 = 0 – общее уравнение прямой
y − y1 , где (x; y) – те- y2 − y1
AB .
Верный ответ № 4.
Задача № 3.2.2
Уравнение прямой (на плоскости), проходящей через точку A(1;2) и составляющей с положительным направлением оси абсцисс угол 45°, имеет вид…
1)x − y + 1 = 0,
2)x + y = 0,
3)x = 0,
4)y + 2 = 0.
Решение
Составим уравнение прямой, проходящей через заданную точку в данном направлении:
y − y0 = k (x − x0 ), k = tg 45° = 1,
y − 2 = 1 (x − 1).
Прямая имеет уравнение:
x − y + 1 = 0.
Верный ответ № 1.
67
Задача № 3.2.3
Нормальным уравнением прямой является…
1) |
2x + 3y + 5 = 0; |
|
|
|
||||||||||||||
2) |
|
|
1 |
|
|
|
x + |
|
3 |
|
y + |
|
5 |
= 0; |
||||
|
|
10 |
|
|
10 |
|
|
10 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3) − |
|
2 |
|
|
x − |
3 |
|
y − |
1 |
|
= 0; |
|||||||
|
13 |
13 |
13 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
4) |
|
x |
+ |
y |
|
= 1. |
|
|
|
|
|
|
|
|
||||
5 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение
Рис. 3.13
Напомним, что нормальное уравнение прямой на плоскости имеет вид:
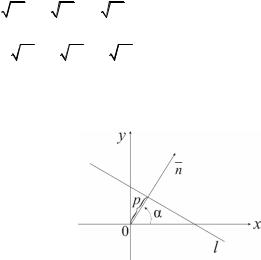
x cos α + y sin α − p = 0,
где α – угол между осью Ox и нормальным вектором прямой, а p –
расстояние от начала координат до прямой l (рис. 3.13).
Таким образом, уравнение первой степени Ax + By + C = 0 является нормальным уравнением прямой, если коэффициенты при x и y являются косинусом и синусом некоторого угла, т.е. для них должно выполняться основное тригонометрическое тождество A2 + B2 = 1 , и, поскольку в нормальном уравнении число p есть расстояние, а рас-
стояние всегда есть число неотрицательное, то свободный член в уравнении Ax + By + C = 0 должен бытьотрицательным.
68

Для уравнения 2x + 3y + 5 = 0 имеем 22 + 32 ≠ 1, следовательно, уравнение не является нормальным.
|
|
Для |
|
|
уравнения |
|
|
|
|
1 |
|
x + |
|
3 |
|
y + |
|
5 |
|
= 0 |
имеем |
|||||||
|
|
|
|
|
|
|
|
10 |
|
|
10 |
|
|
10 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
2 |
|
3 |
2 |
|
p = |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
+ |
|
|
= 1, |
но |
|
|
|
|
> 0 , следовательно, уравнение не |
|||||||||||||||
|
|
10 |
|
|
|
10 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
является нормальным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Для |
|
|
уравнения |
|
− |
|
2 |
|
x − |
3 |
|
y − |
1 |
|
= 0 |
имеем |
||||||||||
|
|
|
|
|
|
13 |
13 |
13 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
2 |
|
|
3 |
|
2 |
|
p = − |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
− |
|
|
|
|
+ |
|
|
= 1 |
и |
|
|
|
|
< 0 , |
следовательно, |
уравнение |
|||||||||||
|
|
|
|
|
|
13 |
||||||||||||||||||||||
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
является нормальным.
Для уравнения |
x |
|
y |
= 1 имеем |
|
1 |
2 |
|
1 |
2 |
|
|
+ |
|
|
5 |
|
+ |
2 |
|
|||
5 |
2 |
||||||||||
|
|
|
|
|
|
|
уравнение не является нормальным.
Верный ответ № 3.
Задача № 3.2.4
Прямая, проходящая через точки A(1;2) и
ось абсцисс в точке с координатой ...
Решение
Составим уравнение прямой AB :
x − 1 |
= |
y − 2 |
; |
||
2 − 1 |
|
0 − 2 |
|||
|
|
||||
x − 1 |
= |
y − 2 |
; |
||
1 |
|
−2 |
|||
|
|
|
|||
−2x + 2 = y − 2; 2x + y = 4.
≠ 1 , следовательно,
B(2;0) , пересекает
69
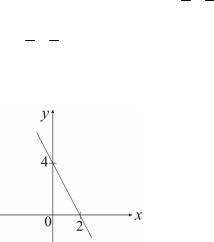
1-й способ
Разделим все члены уравнения на 4, получим 2x + 4y = 1 – урав-
нение прямой в отрезках ( ax + by = 1 ), где a = 2 – величина отрезка,
отсекаемого прямой на оси Ox , а b = 4 – величина отрезка, отсекаемого прямой на оси Oy .
Рис. 3.14
Прямая пересекает ось абсцисс в точке с координатой x = 2 .
2-й способ
Если прямая пересекает ось Ox , то ордината точки пересечения равна нулю. Следовательно, 2x = 4 , x = 2 .
Ответ: 2.
Задача № 3.2.5
Если прямая проходит через точки A(2;5) и B(−4;2) , то тан-
генс угла наклона прямой к оси Ox равен...
Решение
Составим уравнение прямой, проходящей через точки A и B :
x − 2 |
= |
y |
− 5 |
; |
−4 − 2 |
|
− 5 |
||
2 |
|
|||
−3(x − 2) = −6( y − 5);
x − 2 y + 8 = 0 – общее уравнение прямой AB .
70
