книги / Тестовый контроль по математике

Пример третьего уровня сложности

Решение:

1) Напишем уравнение плоскости α, перпендикулярной прямой l, проходящей через точку Р. Заметим, что направ-

A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0 имеет вид 3(x −1) + 2( y +1) −

−2(z + 2) = 0 или в общем виде α: 3x + 2 y − 2z − 5 = 0.

2) Найдем точку A пересечения плоскости α и прямой l. Для этого запишем уравнения прямой l в параметрическом виде: x = −3 + 3t; y = −2 + 2t; z = 8 − 2t и подставим в уравнение плос-

кости α: 3(−3 + 3t) + 2(−2 + 2t) − 2(8 − 2t) − 5 = 0 t = 2. Подста-

вим t = 2 в параметрические уравнения прямой l и получим ко-

плоскость α перпендикулярна прямой l, то искомое расстояние d = PA = (3 −1)2 + (2 +1)2 + (4 + 2)2 = 4 + 9 + 36 = 49 = 7.

Ответ: d = 7.

Возможны ошибки при написании уравнения плоскости и при вычислении координат точки пересечения прямой и плоскости.

71

Тест по модулю «Аналитическая геометрия»

Время прохождения – 60 мин. Задания 1-го уровня сложности: 1–12; задания 2-го уровня сложности: 13–18; задания 3-го уровня сложности: 19–20.

Оценка «удовлетворительно» ставится за 12–15 правильно решенных заданий;

оценка «хорошо» ставится за 16–18 правильно решенных заданий;

оценка «отлично» ставится за 19–20 правильно решенных заданий.

1. Прямая y = x +1 расположена к оси ОX под углом…

72

6. Плоскость Р: 3x + 2y + 1 = 0 перпендикулярна вектору…

9.Уравнение прямой, проходящей через точки A (1; –2; 1)

иB (3; 1; –1), имеет вид…

10. Координатыцентраокружности (x + 2)2 + y2 = 25 равны…

13. Уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметричны относительно начала координат на расстоянии 10 см друг от друга, а расстояние между вершинами равно 6 см, имеет вид…

73

14. Уравнение параболы, проходящей через начало координат, с осью параллельной оси OX и проходящей через точку

B (–1; 3), имеет вид…

19. Расстояние между параллельными сторонами ромба, диагонали которого совмещены с осями координат и равны

74

20.Даны вершины треугольника A (1; –2; –4), B (3; 1; –3)

иC (5; 1; –7). Параметрические уравнения высоты треугольника, опущенной из вершины B на сторону AC, имеют вид…

75

МОДУЛЬ 3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

ОДНОЙ ПЕРЕМЕННОЙ

РАЗДЕЛ «ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ»

Справочные материалы

Пусть функция y = f (x) определена в окрестности некоторой точки x = a, за исключением, быть может, самой точки а.

Определение (на языке «ε – δ »). Число А называется пределом функции y = f (x) при х→ а, если для любого ε > 0 можно указать такое δ = δ (ε ) > 0, что для всех х, удовлетворяющих соотношению |x – a| < δ , имеет место неравенство |f (x) – A| < ε . Тот факт,

1)lim( f (x) ± q(x)) = A ± B ;

x→ a

2)lim f (x)iq(x) = AiB ;

x→ a

3) lim f (x) = A (при условии, что В ≠ 0). x→ a q(x) B

Непрерывность функции в точке

Определение. Функция y = f (x), определенная в некоторой окрестности точки а, называется непрерывной в точке а, ес-

ли lim f (x) = f (a).

x→ a

76

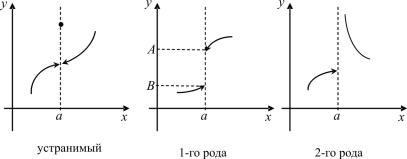
Точки разрыва

Определение. Если функция y = f (x) определена в некоторой выколотой окрестности точки а или не является непрерывной в точке а, то говорят, что точка х = а есть точка разрыва функции f (x).

Точка х = а является точкой разрыва функции f (x) в одном из следующих случаев:

1. Односторонние пределы f (x) при х→ а существуют, конечны, равны между собой, но не равны значению функции в точке х = а. В этом случае точку х = а называют точкой устра-

х = а называется точкой разрыва 1-го рода. Значение (А – В) – скачок функции.

3. Хотя бы один из односторонних пределов не существует или равен бесконечности. В этом случае точка х = а – точка разрыва 2-го рода.

При решении задач полезно помнить таблицу простейших пределов:

77

называть неопределенностями.

Примеры тестовых заданий с решениями к разделу «Предел и непрерывность функции одной

переменной»

Примеры первого уровня сложности

Ввыражении lim Pn (x) , где Pn (x) – многочлен и Qm (x) –

x→∞ Qm (x)

многочлен, мы встречаемся с отношением двух бесконечно больших величин. При вычислении предела необходимо избавиться в числителе либо в знаменателе от бесконечно большой величины. Для этого делим числитель и знаменатель дроби на старшую степень числителя (либо знаменателя).

Решение. Делим числитель и знаменатель на старшую степень числителя х5:

78

Величина, обратная бесконечно малой, есть бесконечно большая.

Неопределённость 0

0

lim f (x) . Пусть f (x) и q (x) – многочлены. Если f (a) = 0

x→ a q(x)

и q (a) = 0, то число а является корнем многочлена f (x) и корнем многочлена q (x), т.е. в разложении многочленов на множители будет присутствовать сомножитель (х – а). Сократив дробь на (х – а), получаем новое выражение, предел которого равен пределу исходного.

метрические функции, обычно используется 1-й замечатель-

ный предел:

79

При вычислении пределов произведения и частного одну бесконечно малую можно заменять ей эквивалентной.

Второй замечательный предел используется для раскрытия неопределенности вида (1∞ ).

80