книги / Некоторые задачи спортивной биомеханики

Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет»

О.Р. Ильялов, Н.С. Шабрыкина, В.А. Лохов, А.В. Сотин

НЕКОТОРЫЕ ЗАДАЧИ СПОРТИВНОЙ БИОМЕХАНИКИ

Утверждено Редакционно-издательским советом университета

в качестве учебного пособия

Издательство Пермского национального исследовательского

политехнического университета

2023

1

УДК 612.76: 796. 012 (075.8) ББК 75.0 Я 73

Н478

Рецензенты:

д-р физ.-мат. наук С.А. Федосеев (Пермский национальный исследовательский политехнический университет);

канд. физ.-мат. наук Ю.В. Баяндин (Институт механики сплошных сред УрО РАН, Пермь)

Некоторые задачи спортивной биомеханики : учеб. Н478 пособие / О.Р. Ильялов, Н.С. Шабрыкина, В.А. Лохов, А.В. Сотин. − Пермь : Изд-во Перм. нац. исслед. политехн.

ун-та, 2023. − 61 с.

ISBN 978-5-398-02855-3

Рассмотрены некоторые задачи биомеханики спорта. Детально рассматриваются уравнения движения спортивного мяча в сопротивляющейся среде. На основе этих уравнений решены практические задачи полета футбольного, волейбольного и теннисного мячей. Рассмотрены элементы фигурного катания – скольжение по дуге и вращение «винт». Изучено движение гимнастической булавы при жонглировании. Учитываются биомеханические особенности человека и реальные условия его движения.

Книга предназначена для студентов, изучающих общий курс теоретической механики и биомеханику спорта.

УДК 612.76: 796. 012 (075.8) ББК 75.0 Я 73

2

4

ПРЕДИСЛОВИЕ

Данное учебное пособие является дополнением к теоретическому курсу по биомеханике спорта. В пособии рассмотрены примеры применения законов теоретической механики для решения задач биомеханики спорта. Учебное пособие соответствует программе по курсу спортивной биомеханики для технических вузов и иллюстрирует курс примерами по игре в футбол, настольный теннис, фигурному катанию и художественной гимнастике. Учитываются биомеханические особенности человека и реальные условия его движения и движение спортивных снарядов. Введение этих примеров способствует лучшему усвоению студентами основного теоретического курса.

Предназначено для студентов высших технических учебных заведений, изучающих биомеханику спорта. Авторы полагают, что рассмотренные в данном учебном пособии биомеханические модели должны получить дальнейшее развитие в сторону их усложнения и рассмотрения новых видов спортивных движений.

5

ВВЕДЕНИЕ

Спортивная биомеханика – это раздел биомеханики, который занимается различными приложениями данной науки в области спорта. Задачами спортивной биомеханики являются не только изучение биомеханических особенностей движений спортсмена с целью улучшения его спортивных результатов, но и изучение влияния других факторов, например спортивного инвентаря, спортивной обуви, погодныхусловий(в частности, ветра) и т.п.

Основой спортивной биомеханики являются механика, а также анатомия и физиология человека. С помощью механического подхода производится анализ движений спортсмена, анализ отдельных масс-инерционных характеристик сегментов тела, анализ движения спортивных снарядов. Биомеханика спорта основана как на методах механики (законах Ньютона, общих теоремах динамики и т.д.), так и на экспериментальных методах. Следует отметить, что механика тесно связана с применением математических концепций, которым также будетуделено внимание вданномучебном пособии.

В пособии достаточно простые биомеханические модели демонстрируют подходы к решению более сложных задач, таких как оптимизация спортивных движений, обеспечение их безопасности, реабилитация травмированных и т.д.

Для чтения предлагаемого пособия надо предварительно изучить курс теоретической механики, включающий в себя статику, кинематику и динамику, хотя некоторые сведения из этих разделов при необходимости приводятся. Изучение общих теорем динамики служит необходимым условием для постановки и решения задач динамики механической системы. Для решения задач биомеханики требуется также знание механических характеристик человеческого тела, и некоторыеизних приведенывтексте.

Учебное пособие написано для студентов, специализирующихся в области биомеханики. Оно также полезно всем, изучающим теоретическую механику по программам технических вузов. Приведенные примеры оживляют курс, позволяют глубже понять законы механики.

6

ГЛАВА 1. ДИНАМИКА МЯЧА

ВСОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ

1.1.Система сил, действующих на мяч. Аэродинамические коэффициенты

лобового сопротивления и подъемной силы

В видах спорта, где используется мяч, важнейшую роль играет траектория мяча, обеспечивающая правильный пас (удар, подачу), и самое главное – поражение ворот соперника, попадание в нужную точку площадки соперника или в нужную лунку (например, при игре в гольф). Использование математических моделей и компьютерного моделирования позволит прогнозировать траекторию полета мяча, а также освоить методику построения таких моделей и научиться реализовывать построенные модели на языке программирования. В данной главе студентам предлагается составить математическую модель движения центра масс мяча. Особенностью описания движения футбольного (волейбольного) мяча является то, что мяч может двигаться с большой скоростью, и в этом случае нельзя применять гидравлическое приближение (например, применяемое в курсе теоретической механики и базовой физики), в котором сила аэродинамического сопротивления пропорциональна квадрату скорости. На основе построенной модели предлагается решить задачу оптимизации, например для нахождения траекторий, наиболее благоприятных для взятия ворот соперника, или под каким углом к горизонту должен вылететь футбольный мяч, чтобы он пролетел наибольшее расстояние по горизонтали.

Будем рассматривать плоские и пространственные траектории движения мяча. На рис. 1 приведена траектория движения мяча в вертикальной плоскости OXY при начальной скорости V0 ,

лежащей в плоскости OXY, вращение мяча происходит вокруг оси, параллельной оси z.

Кинематические характеристики движения – вектор скорости поступательного движения V , направленный по касательной

7

к траектории центра масс, и вектор угловой скорости ω , направленный по оси вращения в ту сторону, откуда вращение видно происходящим против часовой стрелки. Вращение может быть произвольным в зависимости от удара по мячу.

y

Q

V

M

R

ωP

x

z

Рис. 1. Система сил, действующих на футбольный мяч при его обратном вращении

При полете мяча на него действуют следующие силы: сила тяжести P = mg , где m – масса мяча, g – ускорение свободного

где ρ – плотность воздуха, S – площадь наибольшего сечения мя-

ча, перпендикулярного V (площадь Миделя), CD и CL – аэродинамические коэффициенты лобового сопротивления и подъемной

8

силы соответственно. Момент сил трения относительно центра масс не учитываем, ввиду его малости, и во время полета вектор угловой скорости считаем постоянным (будет показано позднее).

Сила тяжести P направлена вертикально вниз. Сила лобового сопротивления R направлена противоположно вектору скорости V :

Сложнее обстоит дело с определением направления подъемной силы Q, обусловленной эффектом Магнуса (1852). Про-

стейшее обоснование этого эффекта состоит в том, что при полете мяча встречный поток воздуха взаимодействует с потоком воздуха, приводимого в движение вращающимся мячом. В зоне смешанных потоков в соответствии с принципом Бернулли образуется область повышенного давления. Так, например, при обратном вращении мяча скорость верхней точки мяча противопо-

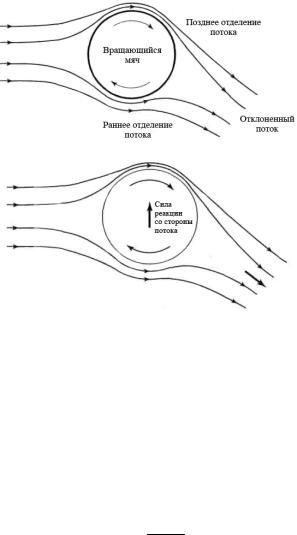
ложна V. Область смешения находится вблизи нижней части мяча, и поэтому возникает подъемная сила. Однако у этого объяснения есть серьезный недостаток – поверхностный слой воздуха, захватываемый вращающимся мячом, достаточно тонок. Поэтому возникающих в нем сил вязкости может быть недостаточно для реализации принципа Бернулли. На рис. 2 представлено другое объяснение эффекта Магнуса. При движении с вращением частицы воздуха захватываются поверхностью мяча. Таким образом, отрыв воздушного потока от поверхности раньше происходит с той стороны, где поверхность мяча движется навстречу потоку воздуха. В результате огибающий мяч поток воздуха отклоняется в сторону (см. рис. 2, а). Но это означает, что и воздух действует на мяч, но уже в противоположном направлении. Для сохранения общего количества движения движение мяча должно быть противоположно движению воздушного потока (рис. 2, б).

9

Термин «подъемная сила» используется и при других направлениях поперечной аэродинамической силы.

а

б

Рис. 2. Объяснение эффекта Магнуса: а – вращение мяча отклоняет поток воздуха; б – возникновение подъемной силы поток воздуха

В эксперименте подъемная сила измеряется как сила, на-

правленная перпендикулярно векторам ω и V . Из опыта также известно, что она направлена в ту сторону, откуда кратчайший

поворот от вектора ω к вектору V виден происходящим против часовой стрелки. Это позволяет применить правило векторного произведения двух векторов:

10