книги / Теория линейных электрических цепей. Ч. 2

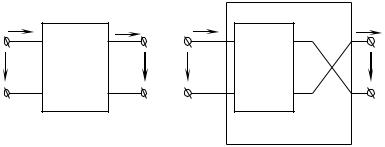
может быть учтено ни расчетом, ни экспериментальным определением сопротивлений в режимах холостого хода и короткого замыкания. Представляется, что возникновение двух решений может также иметь иное объяснение. Изменение полярности выходного тока и напряжения, схемно реализуемое в виде перекрещивания выходных зажимов, образует новый четырехполюсник, характеризующийся своей схемой замещения и матрицей [А]. Таким образом, возникает понятие родственных четырехполюсников, одновременно удовлетворяющих одним и тем же значениям входных сопротивлений Z1х, Z2х, Z1k, Z2k. И в этом отношении такие четырехполюсники равноправны. У всех коэффициентов матрицы [А](2) родственного четырехполюсника знаки меняются на противоположные по отношению к коэффи-

циентам матрицы [А](1).

Схемы замещения родственных четырехполюсников различны, а их соответствие друг другу с точки зрения передающих свойств можно проиллюстрировать с помощью рис. 2.6.

Рис. 2.6

Следует отметить, что схемная реализация родственных четырехполюсников в ряде случаев невозможна, так как в результате расчета параметров схем замещения могут быть получены отрицательные значения активных сопротивлений.

71

2.9. Характеристические параметры четырехполюсника

Для несимметричных четырехполюсников можно подобрать такую пару сопротивлений Z1C и Z 2C , для которых соблюдаются следующие условия:

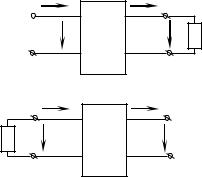
1. Входное сопротивление со стороны выводов 1–1 Z1вх Z1C , если к выводам 2–2 подключено сопротивление

Z 2 Z 2C (рис. 2.7, а).

2. Входное сопротивление со стороны выводов 2–2 Z 2вх Z 2C , есликвыводам1–1 подключеносопротивление Z1 Z1C (рис. 2.7, б).

Z1C и Z 2C называют характеристическими сопротивле-

ниями (характеристическими параметрами) четырехполюсника. Выразим Z1C и Z 2C через А-параметры. Для этого воспользуемся уравнениями (2.9) и (2.11):

72

При выводе этого соотношения числитель и знаменатель дроби разделили на I2 и учли, что Z 2 Z 2C U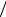2 I2 .

Из уравнений (2.11) следует, что

При выводе соотношения (2.24) числитель и знаменатель дроби разделилина I1 иучли, чтопри принятыхусловиях Z 1C U1 I1 .

Решая совместно уравнения (2.23) и (2.24) относительно Z1C

Третьим характеристическим параметром четырехполюсни-

ка является постоянная передачи (или мера передачи), которая характеризует четырехполюсник как элемент, через который передается мощность, и в общем случае представляет собой комплексное число:

где – постоянная ослабления; – постоянная фазы.

Постоянная передачи должна удовлетворять условиям:

73

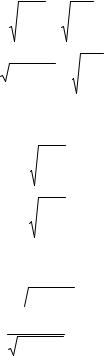
Эти выражения непротиворечат соотношению (2.10), таккак

ch2 sh2 1 .

Z1C , Z 2C , называют вторичными параметрами четырех-

полюсника. Эти величины независимы друг от друга и являются функциями параметров четырехполюсника.

2.10. Уравнения четырехполюсника в гиперболических функциях

Выразим с помощью характеристических параметров соотношения между напряжениями и токами на входе и выходе четырехполюсника. С этойцельюразделимиумножим(2.25) на (2.26):

74

Таким образом, с помощью уравнений (2.33) – (2.36) можно выразить А-параметры через характеристические параметры четырехполюсника. Дляэтого(2.33) – (2.36) подставимв(2.9), тогда:

U2 , I2 связаны друг с другом с помощью трех независимых ха-

рактеристических параметров. Поскольку в эти соотношения входят гиперболические функции, то они называются уравнения-

ми четырехполюсника в гиперболических функциях.

2.11. Режим согласованной нагрузки четырехполюсника

Подключимквыходнымвыводамчетырехполюсника Z 2 Z 2C , тогда Z1вх Z1C . Это соответствует согласованному режиму – режиму передачи максимальной мощности. В этом случае U2 I2 Z 2C . Вынесем в(2.37) U2 , ав (2.38) I2 за скобкии получим:

75

Уравнения (2.39), (2.40) называют уравнениями четырехполюсника для согласованного режима. Найдем произведение

Приведенные соотношения позволяют пояснить физический смысл A и B: A – постоянная ослабления (коэффициент затуха-

ния), учитывает изменение полной мощности сигнала при прохождении через четырехполюсник; B – постоянная фазы (коэффициент фазы), показывает изменение фазы напряжения и тока при прохождении сигнала от первичных выводов к вторичным. Значения и можно определить из уравнений:

76

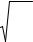
Связь между напряжениями и токами на входе и выходе четырехполюсника можно выразить с помощью двух характеристических сопротивлений и меры передачи.

В симметричных четырехполюсниках A11 A22 , тогда на ос-

новании (2.25), (2.26)

Для симметричного четырехполюсника характеристическое сопротивление Z C называют повторным. Это объясняется тем,

что при Z 2 Z C входное сопротивление со стороны входных выводов тоже будет равно Z C ,

На основании (2.37) и (2.38) для симметричных четырехполюсников

Если у симметричного четырехполюсника в качестве нагрузки использоватьсопротивление Z 2 Z C , то согласно (2.39), (2.40)

В этих соотношениях четко просматривается физический смысл постоянной ослабления и фазы.

77

рах. 1 непер соответствует уменьшению модуля напряжения или тока в e раз при прохождении тока от входных выводов к выходным в симметричном четырехполюснике, нагруженном на Z C .

Постоянная фазы измеряется в радианах или градусах. Применяются и другие единицы измерения ослабления – белы и децибелы. Постоянная в белах определяется по формуле

где S1, S2 – полные мощности соответственно на входе и выходе четырехполюсника.

Для симметричного согласованного четырехполюсника

В этом случае постоянная ослабления (в белах)

2.12. Передаточные функции четырехполюсника

Токи и напряжения могут быть выражены через токи и напряжения со стороны входа и выхода с помощью передаточных

отношение комплексных амплитуд или комплексных действую-

78

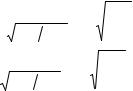
щих значений электрической величины на выходе и входе четырехполюсника при заданном режиме нагрузки. Выразив эти коэффициенты через А-параметры, получим коэффициент передачи

(или передаточную функцию) по напряжению:

и коэффициент передачи по току

Если четырехполюсник нагружен на характеристическое сопротивление, то в соответствии с (2.39), (2.40)

Модули этих величин представляют собой амплитудно-час- тотные характеристики (АЧХ), а их аргументы – фазочастотные характеристики (ФЧХ).

Используются и такие передаточные функции, как переда-

точное сопротивление:

79

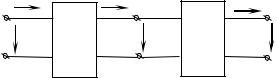
2.13. Соединения четырехполюсников

Рассмотрим три вида соединения четырехполюсников – каскадное (цепная схема соединения, рис. 2.8), параллельное (рис. 2.10)

и последовательное(рис. 2.11).

2.13.1. Каскадное соединение

Пусть в цепной схеме соединения заданы А-параметры четырехполюсника (АI) и (АII). Выразим напряжение и ток на входе четырехполюсника заданными напряжениями и токами на выходе последнего четырехполюсника (в данном случае второго). Для первого и второго четырехполюсников справедливы следующие соотношения:

Рис. 2.8

80