книги / Переработка полимеров

Так как dm dV , получим

Будем предполагать, что накопления материала внутри объема не происходит, т.е. = const, а выражение d 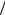dt в (2.7) рав-

но нулю.

Для перехода от поверхностного интеграла к объемному используем теорему Остроградского–Гаусса

Поскольку интеграл равен нулю, а dV является малым и виртуальным, то можем приравнять подынтегральное выражение нулю.

ρd FV 0 Px Py Pz . dt x y z

Так как массовые силы в рассматриваемых задачах значительно меньше поверхностных, то ими будем пренебрегать (FV = 0).

зор, отвечающий за изменение объема, р – гидростатическое давление; ij – девиатор (девиаторный тензор) отвечает за изме-

нение формы.

Пользуясь численной нумерацией координат, проекций векторов и компонент тензоров, можно представить уравнения (2.11) в компонентной компактной форме:

Уравнения (2.11) и (2.12) имеют форму второго закона Ньютона. Они показывают, что скорость изменения количества движения системы равна сумме сил, действующих на неё.

23

2.4. Уравнение энергии

При выводе этого и предыдущих уравнений используют метод математической физики, который исходит из того, что ограничивается промежуток времени и из всего пространства выделяется лишь элементарный объём. Это позволяет в пределах элементарного объёма и малого отрезка времени пренебречь изменением некоторых величин и существенно упростить задачу.

Выбранные таким образом элементарные dV и d с математической точки зрения являются величинами бесконечно малыми, а с физической точки зрения – величинами ещё достаточно большими, чтобы в их пределах можно было бы игнорировать дискретное строениесредыирассматриватьсреду как сплошную.

При выводе дифференциального уравнения энергии сделаем следующие допущения:

–материал однородный и изотропный;

–теплофизические характеристики постоянны;

–внутренние источники тепла распределены по объему равномерно.

В основу вывода дифференциального уравнения теплопроводности (энергии) положен закон сохранения энергии, который в рассматриваемом случае может быть сформулирован таким образом.

Количество тепла, подведенное к элементарному объёму

dV за время d (dQ*), равно изменению внутренней энергии вещества (dU), содержащегося в данном объёме за время d .

dQ*

Для нахождения составляющих уравнения (2.13) выделим в теле параллелепипед со сторонами dx, dy, dz. Грани параллелепипеда параллельны соответствующим координатнымплоскостям.

Количество теплоты, которое подводится к граням элементарного объёма за время d в направлении осей Ox, Oy, Оz, обозначим dQx, dQy, dQz (рис. 2.4).

24

Общее количество тепла, поступившего извне dQ dQx dQy dQz .

Рис. 2.4. Баланс потоков тепла в элементарном объеме

Введем понятие потока тепла: qx – количество тепла, проходящего в единицу времени через единицу площади (в данном

Разница между количеством теплоты, подведённым к dV за d и отведённым в направлениях Ox, Oy, Oz, может бытьвыраженакак

Функция qx dx считается непрерывной в рассматриваемом объёме и может быть разложена в ряд Тейлора.

Ограничимся в выражениях (2.15) только двумя первыми членами ряда и подставим слагаемые в (2.14), получим

dQx qxx dxdydzd qxx dVd , dQy qyy dxdydzd qyy dVd , dQz qzz dxdydzd qzz dVd .

Общее количество теплоты, подведённое к dV за d ,

Определим вторую составляющую уравнения (2.13). Обозначим количество теплоты, выделяемое внутренними

источниками тепла в единице объёма среды за единицу времени и называемое мощностью внутренних источников тепла, че-

dQV qV dVd .

Третья составляющая уравнения (2.13) находится для изохорного процесса (процесс, протекающий без изменения объема)

26

dU c T d dV ,

где с – теплоемкость*; – плотность.

Запишем уравнение (2.12) с учетом полученных слагаемых.

лового потока в направлениирассматриваемыхосей координат.

Аналогичные выражения получим для направлений вдоль оси y,z. Подставляя полученные члены в (2.16), запишем:

T qV c T – уравнение теплопроводности, (2.17)

где

T 2T 2T 2T .x2 y2 z2

В общем случае теплопереноса (с учётом конвективного и диффузионного механизмов переноса тепла) компоненты теплового потокаqx, qy, qz могутбыть представлены следующимобразом:

* Теплоемкость – количество энергии, необходимое для увеличения температуры тела массой 1 кг на 1 С, [Вт/кг С].

27

qx T c xT ,x

qy T c yT , (2.18)

y

qz T c zT.z

Подставив (2.18) в (2.16), получим уравнение энергии

Окончательный вид уравнения энергии

В левой части уравнения (2.19) конвективный теплообмен;T – молекулярный (диффузионный перенос тепла).

2.5.Тензор скоростей деформаций. Реологические уравнения

Напряжённое состояние среды связано и определяется деформационными изменениями. Так, например, под воздействием одной и той же растягивающей силы различные материалы получают различные уд-

Рис. 2.5. Схема нагружения линения.

28

Связь напряжений и деформаций для твёрдых тел осуществляется с помощью закона Гука

Å , l1 l2 , l1

где E – модуль упругости, l1,l2 –конечная и начальная длина образцов, – деформация, – напряжения.

Для жидких сред (растворы и расплавы полимеров) тензор напряжений (или напряжённое состояние в точке среды) зависит от скорости течения среды. Кинематическое соотношение, характери-

зующеедвижение жидкости, – это градиент скорости i .

xi

Причём чем сильнее изменяется величина скорости по сечению канала, тем большее усилие действует на среду, тем большее напряжение в среде возникает.

В общем случае течения возможно более чем одно ненулевое значение градиента скорости. Каждый из трёх компонент скорости может изменяться в трёх координатных направлениях, что даёт девять возможных компонент градиента скорости. Таким образом, можно ввести тензор градиентов скорости , который в декартовых координатах запишется как

В общем случае движение среды, описываемое тензором градиентов скоростей, представляет собой одновременно поступательное и вращательное движение. Такие движения можно разделить, представить тензор градиентов градиентов в виде двух слагаемых:

29

12 ,

где и – тензорскоростейдеформациии вращательный тензор. Тензор скоростей деформаций , отвечающий за поступа-

тельное движение, вводится следующим образом:

T ,

где тензор T – транспонированный тензор, имеющий те же компоненты, что и , но с переставленными индексами (зеркальное отображение компонент относительно главной диагонали тензора скоростей деформаций).

Уравнениями состояния, или реологическими уравнениями, называют уравнения, связывающие тензор напряжений и тензор скоростей деформаций, т.е. ~ .

В том случае, если связь между этими тензорами линейна, то говорят, чтожидкость является ньютоновской, или линейной.

Если ньютоновская жидкость помещена между двумя параллельными бесконечными пластинами и одна из пластин движется с постоянной скоростью, то после достижения установившегося течения сила на единицу площади, приводящая в движение пластину, пропорциональна скорости движения пластины и обратно пропорциональна расстояниюмежду пластинами.

FS ~ Hz .

30