
книги / Основы конденсаторной техники
..pdfиметь место и в неорганических диэлектриках типа керамики и слюды.
Метод испарения металла в вакууме. Заключается в на-
греве металла в вакуумной камере, испарение его и осаждение паров металла на поверхности диэлектрика тоже находящегося в вакуумной камере. Применение вакуума обеспечивает отсутствие окисления испаряемого металла, снижение его точки кипения и получение прямолинейного движения атомов металла от испарителя к поверхности диэлектрика. Этот метод пригоден для органических и неорганических диэлектриков. Метод испарения в вакууме широко применяется для серебрения слюды. При атмосферном давлении температура кипения се-
ребра равна 1955 °С, а при давлении 10−2 мм рт. ст. – 1050 °С. Этот способ позволяет получать слюдяные конденсаторы высокого качества. При металлизации органических диэлектриков, имеющих вид длинных тонких лент, намотанных в рулоны (конденсаторная бумага, синтетические пленки), процесс ведут непрерывно, пропуская ленту над испарителем. После окончания металлизации вакуум снимают и достают металлизированный рулон (в качестве металла используют цинк и алюминий). Производят как одностороннюю металлизацию, так и двухстороннюю, исключающую воздушный зазор между обкладками и диэлектриком.
Метод катодного распыления металла. Применяется,
когда высокая температура кипения тугоплавкого металла не позволяет успешно применить метод испарения в вакууме. Катодом является испаряемый металл, анодом – подложка, на которую наносится слой металла. В вакуумную камеру после откачки подают инертный газ. Этот метод используют редко, так как мала скорость создания металлического слоя; применяют в основном в производстве тонкопленочных конденсаторов с неорганическим нагревостойким диэлектриком, требующих применения обкладок из тугоплавкого металла.
61
11. Особенности металлизированного диэлектрика
При замене обкладок из фольги тонким слоем металла, нанесенным тем или иным методом на поверхность диэлектрика, в конденсаторе возникают некоторые явления, которые не наблюдались при обкладках из металлической фольги. К числу этих явлений относятся: явление мерцания емкости; явление самовосстановления конденсатора при пробое.
Явление мерцания емкости было обнаружено для кера-
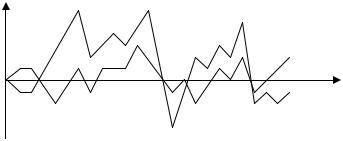
мических и слюдяных конденсаторов с серебряными обкладками, нанесенными методом вжигания и испарением в вакууме. Это явление характеризуется небольшими самопроизвольными скачками емкости, вызывающими соответствующие скачки частоты контуров (рис. 31). Величина таких скачков невелика, но возрастает с увеличением напряжения, что может отражаться на стабильности работы.
C
τ, с
─U1 ---U2>U1
Рис. 31. Мерцание емкости конденсатора
Была разработана специальная методика для отбраковки конденсаторов, в которых наблюдалось это явление. Брак «по мерцанию» можно снизить, увеличивая толщину диэлектрика в конденсаторах, т.е. снижая рабочее значение напряженности поля.
Явление мерцания связано с отсутствием четко выраженного края серебряного электрода и наличием большого чис-
62
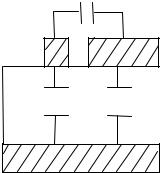
ла мелких островков серебра, постепенно соединяющихся в сплошную обкладку по мере удаления от закраин, свободных от серебра
(рис. 32).
В схеме, эквивалентной «мерцающему» конденсатору: С1 – ос-
новная емкость электрода; С2 – емкость островка; С3 – емкость тон-
кого зазора между островком и основной обкладкой.
При высокой температуре по системе емкостей С2 –С3 проходит
С3
С2 С1
Рис. 32. Схема «мерцающего» конденсатора
ток, создающий основное падение напряжения на емкости зазора, так как С3 << С2. При этом в зазоре возникает микроду-
га, присоединяющая С2 к С1, что дает скачкообразное увели-
чение емкости конденсатора. При обрыве дуги емкость скачкообразно уменьшается. Погружение в жидкий диэлектрик не устраняет мерцания, увлажнение усиливает его.
Явление мерцания приводит к небольшому увеличению емкости конденсаторов с напряжением. Этим увеличением можно пренебречь, за исключением случаев, когда точность емкости играет особо большую роль (образцовые конденсаторы).
Явление мерцания связано и с увеличением потерь энергии в конденсаторе.
Явление самовосстановления в конденсаторе. Конден-
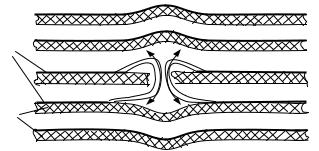
саторы с металлизированными обкладками восстанавливают электрическую прочность диэлектрика после пробоя. В зоне пробоя ток короткого замыкания достигает максимальной плотности и испаряет (выжигает) тонкий слой металла в окрестности этой зоны (рис. 33). Электрическая дуга увеличивает свою длину и гаснет, так как в зоне пробоя давления растет за
63
1
3
2
Рис. 33. Схема, поясняющая процесс самовосстановления при пробое: 1 – обкладки; 2 – диэлектрик; 3 – электрическая дуга
счет газообразных продуктов разложения диэлектрика и пропитки. Вокруг места пробоя образуется свободный от металлических обкладок участок диэлектрика малой площади (от долей до 10 мм2). Этот процесс происходит за короткое время –
приблизительно 10−4...10−5 с. Выделяющаяся при этом энергия не вызывает существенного повреждения диэлектрика, лишь в месте пробоя остается тонкое отверстие диметром 1…10 мкм. Таким образом, тонкие обкладки играют роль предохранителя, отключающего поврежденный участок диэлектрической системы. При этом емкость конденсатора почти не меняется. Емкость металлобумажного конденсатора С = 1,5 мкФ уменьшается на 1 % после 105 пробоев.
Пленочные конденсаторы с металлизированными обкладками более чувствительны к самовосстановлению и выходят из строя раньше. Это явление связано с составом пленочного диэлектрика, в частности, с относительным содержанием кислорода в его молекуле.
64
12. Потери энергии в конденсаторе
Всякий реальный конденсатор, включенный в электрическую цепь, рассеивает электрическую энергию. Эта энергия расходуется на нагрев конденсатора.
Потери энергии в конденсаторе складываются из следующих составляющих:
1. Потери энергии в диэлектрике конденсатора Pд:
а) от движения ионов (проводимость, междуслойная поляризация, ионно-релаксационная поляризация);
б) от вращения диполей и перемещением полярных групп (дипольная, дипольно-радикальная, спонтанная поляризации); в) от ионизации воздушных включений в диэлектрике или
воздуха у края обкладок.
2. Потери энергии в металлических частях конденсатора Pм:
а) от нагрева током контактов и выводов; б) от нагрева током обкладок;
в) от явления мерцания у краев обкладок, полученных металлизацией диэлектрика;
г) от вибрации обкладок.
Полные потери энергии в конденсаторе (активная мощность)
Ра = Рд + Рм.
Величина потерь опасна, так как выделяемое тепло может привести к недопустимому повышению температуры конденсатора.
При установившемся тепловом состоянии конденсатора количество тепла, выделяющееся в нем за 1 с, должно быть равно количеству тепла, отводимому в 1 с от его поверхности в окружающую среду:
Ра = αт S (tк −tо ),
65

где αт – коэффициент теплоотдачи, Вт/(м2·°С);
S – поверхность охлаждения конденсатора, м2; tо – температура окружающей среды, °С;
tк – температура конденсатора, °С.
Перегрев конденсатора прямо пропорционален величине потерь:
∆tR =tк −tо = αРт аS .
13. Расчет величины потерь в конденсаторе при синусоидальном напряжении
Потери энергии в основном диэлектрике Рд1 (Вт) рассчитываются по формуле
P |
= 2π U 2 f C tg δ |
, |
(15) |
д1 |
д |
|
|
где U – эффективное напряжение, В; f – частота, Гц;
С – емкость, Ф;
tg δд – тангенс угла потерь основного диэлектрика. Мощность Pд2 , теряемая во вспомогательном диэлектри-
ке, может быть рассчитана по формуле (15), если в нее подставить значение паразитной емкости Сп и величину tg δп вспо-
могательного диэлектрика. Если в конструкции использовано несколько вспомогательных диэлектриков (заливочная масса, изоляция корпуса, пластмассовая опрессовка, выводные изоляторы), то для каждого из них надо брать значение созданной им части общей паразитной емкости и соответствующие ему значение tg δ.
Тогда общие диэлектрические потери конденсатора
Р = Р + Р = 2π U 2 f |
C tg δ + ∑C tgδ . |
|||
|
|
|
i=n |
пi |
д д1 д2 |
д |
пi |
||
|
|
|
i=1 |
|
66

Для уменьшения потерь необходимо выбрать основной диэлектрик с малым tg δ, а также и вспомогательные диэлек-
трики с малым tg δ. Нужно тщательно освобождать конденса-
тор от остатков воздуха, чтобы устранить потери от ионизации воздушных включений, внутри диэлектрика и у края обкладки.
Мощность, теряемая на нагрев металлических выводов конденсатора. Для подсчета мощности, теряемой на нагрев металлических выводов, используют формулу
|
Р = r I 2 , |
|
в в |
где I |
– ток, потребляемый конденсатором, А; |
rв |
– сопротивление выходов, Ом. |
Ток, протекающий в конденсаторе, можно вычислить по формуле
I = |
U |
=U ω C или I = U . |
|
χ |
|
||
|
С |
Z |
|
|
|
|
|
Мощность тепловыделения в одном выводе конденсатора круглого сечения при сильном поверхностном эффекте
(∆< 0,1dв )
Pв = I 2 dв πlвγм ∆,
где dв, lв – диаметр и длина вывода;
γм – удельная проводимость металла;
∆ – глубина проникновения электромагнитного поля в металлический вывод,
∆ = |
1 |
, |
|
||
π f γм µ0 µ |
µ0 = 4π 10−7 Гн/м.
67
При слабом поверхностном эффекте (∆≥ 0,1dв ) мощность определяется по формуле
|
|
|
|
|
Pв = I |
2 |
|
|
4 lв |
|
|
. |
|
|
||
|
|
|
|
|
|
dв2 π γм |
|
|
||||||||
|
Более точное значение мощности потерь |
|||||||||||||||
|
|
|
|
Р = I 2 |
|
4lв |
|
K |
|
|
dв |
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
в |
|
π γм dв |
|
|
|
|
||||||
|
|
|
|
|
|
|
2∆ |
|
||||||||
где |
K |
dв |
|
– коэффициент, определяемый по графику и учи- |
||||||||||||
|
||||||||||||||||
|
2∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тывающий изменение сопротивления за счет поверхностного эффекта.
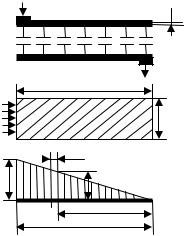
Мощность, теряемая на нагрев обкладок. При вычисле-
нии мощности, теряемой на нагрев обкладок, нужно учесть изменение тока по длине обкладки.
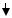 δоб
δоб
|
l |
|
b |
|
dx |
I |
Ix |
|
|
|
x |
|
l |
|
Рис. 34. Схема к расчету мощ- |
|
ности, теряемой в обкладках |
Рассмотрим плоский конденсатор с выводами в конце каждой обкладки (рис. 34). Обозначим: l – длина обклад-
ки; b – ширина обкладки; δоб – толщина обкладки; ρ – удель-
ное сопротивление металла обкладки.
В том конце обкладки, где поставлен вывод, ток равен I, далее он спадает линейно и в противоположном конце равен 0.
Выделим элемент обкладки длиной dx на расстоянии х от того конца, где ток равен 0.
68

Сопротивление этого элемента
rx =ρ bdx .
δоб
Ток в этом элементе
Ix = I xl .
Расход мощности на нагрев элемента
P = r I |
2 |
= |
ρ I 2 |
2 |
|
|
|
x |
|
x |
|
dx. |
(16) |
||
|
|
||||||
x x |
|
l2 b δоб |
|
|
|
||
|
|
|
|
|
|
||
Для того чтобы получить величину мощности, теряемую во всей обкладке, надо проинтегрировать это выражение по длине обкладки и умножить на 2, так как обкладки две:
l |
|
2ρ I 2 |
l |
2 |
|
2l |
|
2 |
|
|
|
Pоб = 2 ∫ Px = |
|
|
|
∫ x |
dx = |
|
ρ I |
|
. |
(17) |
|
l |
2 |
|
3b δоб |
|
|||||||
0 |
|
b δоб 0 |
|
|
|
|
|
|
|||
Если учесть часть длины обкладки ∆l, выступающую за пределы активной площади, и понимать под значением l только активную длину обкладки, то имеем
∆l + 3l
Pоб = 2 b δоб ρ I 2.
Мощность, теряемую в обкладках цилиндрического конденсатора, можно найти по формуле (16), выразив ширину обкладки как среднюю длину окружности l = π Dср, где Dср –
среднее значение диаметра цилиндрического конденсатора. Для плоского многопластинчатого конденсатора с числом
обкладок N имеем
|
(2N −3) |
|
∆l + |
l |
|
||
|
|
|
|
|
|||
|
3 |
||||||
P = 2 |
|
|
|
|
ρ I 2. |
||
(N −1)2 b δоб |
|
||||||
об |
|
|
|||||
69
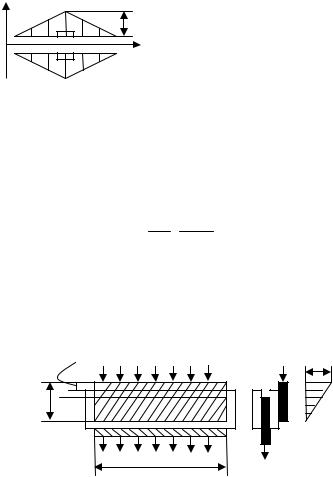
Р |
Если выводы поставлены |
||
|
|
I/2 |
в середине намотки спирального |
|
|
х |
конденсатора (рис. 35), то потери |
|
|
||
|
|
|
уменьшаются в 4 раза и выража- |
|
|
|
|
|
|
|
|
|
|
|
ются формулой |
Рис. 35. Схема расположе- |
P = |
l |
ρ I 2. |
|
ния выводов в середине дли- |
||||
|
||||
ны обкладок |
об |
6b δоб |
||
При большой длине ленты фольги ставят несколько пар выводов – n и, если они расположены равномерно, то мощность, теряемая в обкладках,
Pоб = 61n2 b lδоб ρ I 2.
При намотке с выступающей фольгой (безындукционной) ток вводится с торцов конденсаторной секции (рис. 36), поэтому ширина фольги определяет длину пути тока, а длина ленты – ширину пути тока.
∆b |
I |
b bа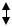
l
Рис. 36. Схема к расчету потерь в обкладках при намотке с выступающей фольгой
Если активная ширина фольги bа и ∆b =b −ba – часть
ширины фольги, определяемая закраиной и необходимостью осуществлять соединение с выводом, то мощность, теряемая в обкладках конденсатора,
70
