книги / Маркшейдерское дело. Анализ точности

венного выполнения ориентировки невозможно правильно и безопасно вести горные работы. В соответствии с этим маркшейдер должен уметь оценить точность ранее проведенной ориентировки, выполнить предрасчет погрешности проектируемой соединительной съемки и на основании этого предрасчета разработать методику ориентировки нового горизонта.

Под погрешностью ориентировки Mор понимается погрешность определения дирекционного угла m 0 первой стороны ОМС. Эту погрешность можно определить по формуле

где Mп – погрешность примыкания к отвесам на поверхности; – погрешность проектирования створа отвесов с поверхности на ориентируемый горизонт; Mш – погрешность примыкания к отвесам на

ориентируемом горизонте (в шахте).

При ориентировании через один вертикальный ствол примыкание к отвесам может быть осуществлено различными способами, главными из которых являются:

–способ соединительного треугольника;

–способсимметричногопримыкания(способпараллельныхшкал);

–способ соединительного четырехугольника;

–примыкание при помощи пентапризмы.

3.5.1.Оценка точности ориентировки первой стороны подземного теодолитного хода при примыкании

к отвесам способом соединительного треугольника

Согласно опросу, проведенному профессором Н.И. Стениным [11] в более чем 150 маркшейдерских отделах, было выявлено, что на горнодобывающих предприятиях используют исключительно способ соединительного треугольника.

Определим последовательно все три составляющие погрешности ориентировки при примыкании к отвесам способом соединительного треугольника (в курсовом проекте это ствол № 1).

21

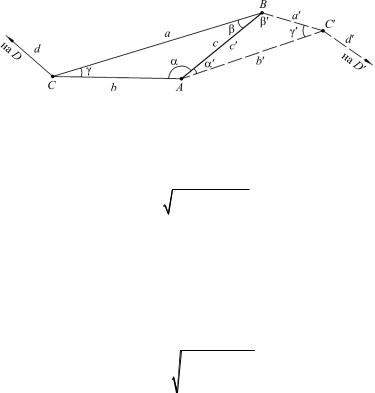
Определение погрешности примыкания к отвесам на по-

верхности. Примыкание на поверхности (рис. 3.6) заключается в передаче дирекционного угла на створ отвесов АВ при помощи примычного угла DCB и угла β при отвесе В. В шахте дирекционный угол со створа отвесов АВ передается на исходную сторону подземной съемки при помощи угла при отвесе А и примычного угла AC D (при этом передача координат с поверхности в шахту не принимается во внимание). Все вычисления, как правило, ведутся с использованием острых углов, так как в треугольнике ошибка острого угла меньше ошибки тупого.

Рис. 3.6. Схема ориентировки при примыкании к отвесам способом соединительного треугольника

Погрешность примыкания на поверхности определяется по формуле

Вычисления производятся в метрах. В формуле (3.19) из углов

и выбирается наименьший.

Всвою очередь, если ошибки центрирования сигнала в точке D

итеодолита в точке С (ed и ec соответственно) равны между собой

где mi – инструментальная ошибка (определяется по формуле (3.14)

или (3.15)); е – линейная ошибка центрирования теодолита в точке С и сигнала в точке D (линейная ошибка центрирования в точке В

22

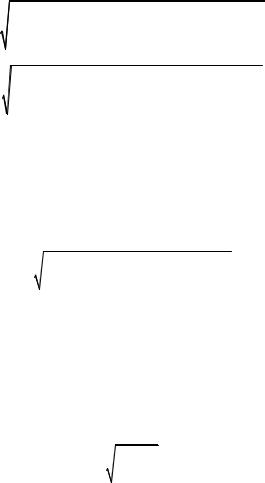
равна нулю, поскольку при измерении угла DCB визируем непосредственно на проволоку отвеса В); d – длина примычной стороны на поверхности (DC).

Ошибку вычисленного угла M при отвесе A и вычисленного угла M при отвесе B можно найти по формулам из работы [5]:

где M – ошибка измерения угла соединительного треугольника

АВС; ma , mb , mc – ошибки измерения сторон a, b, c соединительно-

го треугольника АCB, определяются по формуле (3.10).

Ошибка измерения угла возникает за счет инструментальной ошибки mi и ошибки центрирования теодолита в точке С:

Определение ошибки проектирования створа отвесов.

На точность проектирования влияют следующие факторы: действие воздушного потока, капеж, схождение отвесов к центру земли, упругость проволоки и др. Вследствие этого створ отвесов на ориентируемом горизонте может составить со створом отвесов на дневной поверхности некоторый угол , который вычисляется по формуле

где e1 и e2 – линейные ошибки проектирования первого и второго отвесов; c – расстояние между отвесами.

23

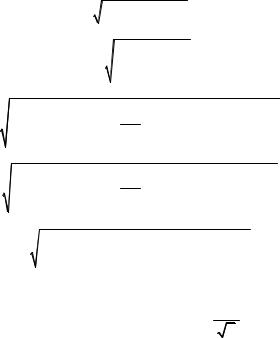
При e1 е2 е

Линейная ошибка проектирования точки не может быть определена непосредственно. Возможно лишь примерное определение этой ошибки из сопоставления результатов геометрического и гироскопического ориентирования подземной съемки. Согласно практике эта линейная ошибка не превышает 1,5–2,0 мм [14].

Определение погрешности примыкания в шахте. Погреш-

ность примыкания в шахте определяется по формулам, аналогич-

ным формулам (3.19)–(3.23):

Ориентировка выполняется независимо дважды [13, п. 163],

и определяется средняя ошибка ориентировки M2ор . Полученную

ошибку нужно сравнить с допустимой по инструкции и сделать вывод о качестве ориентирно-соединительной горизонтальной съемки способом соединительного треугольника.

24

3.5.2. Определение ошибки ориентировки ствола при примыкании к отвесам с помощью параллельных шкал

(симметричный способ)

Способ симметричных шкал можно применять при примыкании к отвесам только в шахте. Поэтому на поверхности примыкание к отвесам осуществляется соединительным треугольником и ошибка примыкания на поверхности вычисляется по формулам (3.19)– (3.23). Если примыкание в шахте производится при помощи параллельных шкал (в курсовом проекте это ствол № 2), то ошибка ориентировки вычисляется по формуле

где Mп – ошибка примыкания к отвесам на поверхности способом соединительного треугольника; Mш – погрешность примыкания к отвесам наориентируемомгоризонте способомсимметричныхшкал.

В этом случае Mш включает в себя погрешность проектирова-

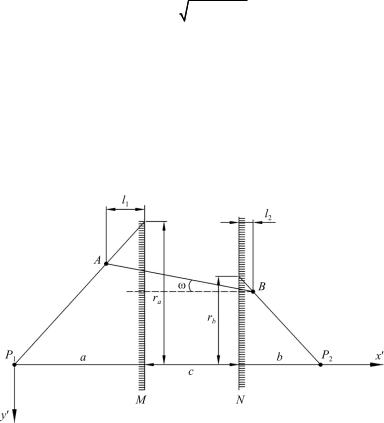
ния створа отвесов, поскольку задачи проектирования и примыкания здесь решаются одновременно. Схема примыкания симметричным способом показана на рис. 3.7.

Рис. 3.7. Схема примыкания симметричным способом

25

Примыкание симметричным способом заключается в передаче дирекционного угла створа отвесов АВ на примычную сторону P1P2 в шахте через угол . В данном случае ошибка примыкания в шахте Мш равна ошибке определения этого угла М . В свою очередь, ошибка угла зависит от ошибок шкальных отсчетов ( ra и rb ), ошибок измерения расстояний от отвесов до шкал ( l1 и l2 ), ошибки

измерения расстояния между шкалами (с) и ошибки измерения расстояний от примычных точек (Р1 и Р2) до шкал (a и b) и определяется по формуле

Влияние ошибок шкальных отсчетов определяется по формулам:

где mra и mrb – ошибки шкальных отсчетов, mra mrb 0,0005 ;

x c l1 l2 .

Влияние ошибок измерения расстояний от отвесов до шкал оп-

стояний от отвесов до шкал, рассчитываются по формуле (3.10). Влияние ошибки измерения расстояния между шкалами опре-

деляется по формуле

26

где mс – ошибка измерения расстояния между шкалами, рассчиты-

вается по формуле (3.10).

Влияние ошибок измерения расстояний от примычных точек до шкал определяется по формулам:

где ma , mb – ошибки измерения расстояний от примычных точек

до шкал.

Ориентировка выполняется независимо дважды [13, п. 163],

и определяется средняя ошибка ориентировки M2ор . Полученную

ошибку нужно сравнить с допустимой по инструкции и сделать вывод о качестве ориентирно-соединительной горизонтальной съемки симметричным способом.

Примечание: маркшейдерская практика применения способа примыкания с помощью параллельных шкал показывает, что в основном ошибку этого способа определяет ошибка шкальных отсчетов ra и rb . Поэтому оценивать точность симметричного примыка-

ния можно по упрощенной формуле:

3.5.3. Оценка точности гироскопического ориентирования

Гироскопическое ориентирование производят специальными приборами – гирокомпасами. Данный метод позволяет с высокой точностью определить азимут направлений.

27

В данном разделе необходимо произвести оценку точности гироскопического ориентирования, пользуясь теоретическими основами, представленными ниже. При этом требуется выбрать гирокомпас, описать требования к гироскопическому ориентированию и методику выполнения работ при гироскопическом ориентировании.

Под точностью гироскопического ориентирования понимается средняя квадратическая погрешность определения дирекционного угла ориентируемой стороны относительно исходной стороны на поверхности. Она зависит от точности гирокомпаса и выбранной методики ориентировки.

Под точностью гирокомпаса понимается средняя квадратическая погрешность m определения гироскопического азимута при одном пуске прибора. Данная величина определяется по формуле

где n – количество взятых отсчетов при определении гироскопического азимута; – уклонение отдельного значения гироскопического азимута от среднего арифметического [6].

Величина m является паспортной характеристикой прибора. При его выпуске с завода погрешность устанавливается экспериментально путем многократных пусков гирокомпаса на одной и той же стороне в разных условиях. Значение ошибки m позволяет достаточно просто оценивать точность определения дирекционного угла при любой методике ориентирования.

Дирекционный угол ориентируемой стороны в шахте определяется из выражения [6]

где п – известный дирекционный угол стороны на поверхности; Гп и Гш – гироскопический азимут соответственно стороны на поверхности и стороны в шахте; – разность сближения меридианов

для точек стояния гирокомпаса на поверхности и в шахте,п ш .

28

Поэтому ошибка определения дирекционного угла гироскопическим способом определяется так:

где mГп и mГш – погрешности гироскопических азимутов соответст-

венно исходной (на поверхности) и ориентируемой (в шахте) сторон. Каждый из этих азимутов в общем случае определяется как среднее арифметическое результатов нескольких пусков прибора.

Погрешности средних значений вычисляются по формулам:

где kп и kш – количество взятых отсчетов при определении гироскопического азимута исходной и ориентируемой сторон.

Подставляя эти выражения в формулу для определения m (3.40), получаем окончательную формулу:

В производственных условиях более целесообразно вычислять погрешность m по разности двойных измерений:

где d – разность двух ближайших определений гироскопического азимута исходной стороны, выполненных в разных условиях (например, до и после работы в шахте); n – число разностей.

3.6. Определение ошибок координат конечной точки свободного полигона

В практике маркшейдерских работ форму полигона определяют горные выработки. Обычно это висячие (свободные) ходы, т.е. ходы, опирающиеся на одну твердую сторону полигона. Под твердой сто-

29

роной понимают сторону, дирекционный угол которой определен. На ошибку координат такого полигона оказывают совместное влияние ошибки ориентирования (ошибки дирекционного угла исходной стороны), ошибки измерения углов и ошибки длин сторон полигона. Для удобства дальнейших вычислений необходимо указанные на плане проектного полигона значения горизонтальных углов с точностью до градуса, длин линий – до метра свести в табл. 3.2.

где M 0 ,M ,Ml – ошибки положения конечного пункта, зависящие

от погрешности определения дирекционного угла, ошибок измерения горизонтальных углов и длин линий соответственно; M x 0

и M y 0 – ошибки координат, обусловленные погрешностью определения дирекционного угла исходной стороны; M x и M y –

ошибки координат, обусловленные ошибками измерения горизонтальных углов; M xl и M yl – ошибки координат, обусловленные

ошибками измерения длин линий.

30