книги / Теория вероятностей и математическая статистика

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

, P(B2 ) =

Условные вероятности

P(A / B1 ) = 0,81

..pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

898.56 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

B4 – в урне был 1 белый и 3 черных шара; B5 – в урне было 4 черных шара.

Формулу полной вероятности используем в следующем виде:

P( A) = P( A / B1 ) P(B1 ) + P(A / B2 ) P(B2 ) +

+P(A / B3 ) P(B3 ) + P(A / B4 ) P(B4 ) + P(A / B5 )P(B5 ).

События B1, B2, B3, B4, B5 образуют полную систему событий, значит, их сумма равна достоверному событию и

P(B1 ) + P(B2 ) + P(B3 ) + P(B4 ) + P(B5 ) =1.

По условию все эти вероятности равны. Следовательно,

P(B1 ) = P(B2 ) = P(B3 ) = P(B4 ) = P(B5 ) = 15.

Общее число элементарных исходов n = C36 =	4 5 6	= 20.
	1 2 3
Находим вероятности гипотез и условные ве-
Находим вероятности гипотез и условные ве-
роятности.			6б
			6б
При B1: m1 = C36 = 20, P( A / B1 ) = 20 / 20 =1.
При B1: m1 = C36 = 20, P( A / B1 ) = 20 / 20 =1.

			3

При В2: m2 = C53 =10, P(A / B2 ) =10 / 20 =1/ 2.	5б
	1ч

4б

2ч

3б

3ч

2б

4ч

При В3: m3 = C34 = 4, P(A / B3 ) = 4 / 20 =1/ 5.

При В4: m4 = C33 =1, P(A / B4 ) =1/ 20.

При В5: m5 = 0, P(A / B5 ) = 0.

По формуле полной вероятности находим

P(A) =1	1		1	1		1	1	1		1			1		1	1+		1		1		1	=
		+			+			+			+ 0			=					+		+
	5	+	2	5	+	5	5	+	20	5	+ 0		5	=	5			2	+	5	+	20
			=	1	20 +10 + 4 +1 =							1		35	=	7	.
			=	5	20 +10 + 4 +1 =							5		20	=	20	.
				5				20				5		20		20

Ответ: Р(А) = 7/20.

Задача 1.8

В одной урне 5 белых и 6 черных шаров, а в другой – 4 белых, 8 черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.

Решение:

1-я урна 2-я урна

5б →3 4б →46ч 8ч

В этой задаче испытания происходят в два этапа: вначале случайным образом вынимают шары из первой урны и опускают во вторую, а затем случайно вынимают шары из второй урны.

Событие А – шары, взятые из второй урны. Рассмотрим события (гипотезы):

B1 – из первой урны вынимают 3 белых шара;

B2 – из первой урны вынимают 2 белых и 1 черный шар; B3 – из первой урны вынимают 1 белый и 2 черных шара; B4 – из первой урны вынимают 3 черных шара.

Вероятность события А находим по формуле

P(A) = P(A / B1 ) P(B1 ) + P(A / B2 ) P(B2 ) +

+P(A / B3 ) P(B3 ) + P(A / B4 ) P(B4 ).

Количество элементарных событий на первом этапе

n1 = C3 = 9 10 11 =165, 11 1 2 3

а на втором этапе

n2 = C4 = 12 13 14 15 =13 7 15. 15 1 2 3 4

Находим вероятности гипотез и условные вероятности.

			m1		= C53 =					4 5				=10,							7б					m2 = C74 = 5 6 7 = 35,
			m1		= C53 =					4 5				=10,							7б					m2 = C74 = 5 6 7 = 35,
При B1 :										1 2											8ч										1 2 3
При B1 :									10					2							8ч												35
			P(B ) =						10			=		2		,										P(A / B ) =							35				.
			P(B ) =									=				,										P(A / B ) =											.
					1			165						33															1			13 7 15
					1																								1


																					4
При B2 :																													4		=		5 6		=15,
																						6б

					= 4 5 6																					m2 = C6							1 2
m1 = C52 С16					= 4 5 6						= 60,											9ч											1 2		15
							1 2 1																			P(A / B2 ) =									15				.
P(B ) =			60		= 12 ,																													13	7 15



2	165						33
	165						33																4
																							4
При B3 :																										m2 = C54 = 5,
																						5б
																						5б
m1 = C15 С62 = 5 5 6											= 75,											10ч				P(A / B ) =									5			.
m1 = C15 С62 = 5 5 6											= 75,															P(A / B ) =								13	7 15			.
						1 1 2																							3					13	7 15
																													3
P(B ) =		75			= 15 ,
		75

3	165				33
	165				33																		4
																							4
			m1				3	=		4 5 6					= 20,											m2 = C44 =1,
																					4б

					= C6					1 2 3																									1
При B4 :										1 2 3											11ч					P(A / B4 ) =
При B4 :																					11ч
			P(B4 ) =					20				=		4			,																	13	7 15			.
			P(B4 ) =									=					,																	13	7 15
								165						33
								165						33

																					4

P(A) =				2				35					+ 12						15		+		15		15			+	4					1		=
P(A) =							13	7 15					+ 12					13	7 15		+		33	13	7 15			+	33		13 7 15					=
	33						13	7 15						33				13	7 15				33	13	7 15				33		13 7 15
							=	70 +180 + 75 + 4 =															329			=		47		.
										33 13 7 15										33 13 7 15							6435
Ответ: Р(А) =												47			.
Ответ: Р(А) =											6435				.
											6435
24

Задача 1.9

Впирамиде стоят 19 винтовок, из них 3 винтовки с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0,81, а стреляя из винтовки без оптического прицела, – с вероятностью 0,46. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.

Решение:

Вэтой задаче первым испытанием является случайный выбор винтовки, вторым – стрельба по мишени. Рассмотрим следующие события:

А – стрелок поразит мишень;

B1 – стрелок возьмет винтовку с оптическим прицелом; B2 – стрелок возьмет винтовку без оптического прицела. Используем формулу полной вероятности.

P(A) = P(A / B1 ) P(B1 ) + P(A / B2 ) P(B2 ).

Учитывая, что винтовки выбираются по одной, находим

P(A / B2 ) = 0,46.

Следовательно, P(A) = 0,81 193 + 0,46 1619 = 0,515.

Ответ: Р(А) = 0,515.

Задача 1.10

В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготови- телями. На складе имеются электродвигатели названных заводов соответственно в количестве 19,6 и 11 штук, которые могут безотказно работать до конца гарантийного срока с вероятностями 0,85;

0,76 и 0,71 соответственно. Рабочий берет случайно один двигатель и монтирует его к устройству. Найти вероятность того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен третьим заводом-изготовителем.

Решение:

Первым испытанием является выбор электродвигателя, вторым – работа электродвигателя во время гарантийного срока. Рассмотрим следующие события:

А – электродвигатель работает безотказно до конца гарантийного срока;

B1 – монтер возьмет двигатель из продукции первого завода; B2 – монтер возьмет двигатель из продукции второго завода; B3 – монтер возьмет двигатель из продукции третьего завода. Вероятность события А вычисляем по формуле полной веро-

ятности:

P(A) = P( A / B1 ) P(B1 ) + P(A / B2 ) P(B2 ) + P(A / B3 ) P(B3 ).

Условные вероятности заданы:

P(A / B1 ) = 0,85,	P(A / B2 ) = 0,76							P( A / B3 ) = 0,71.
Найдем вероятности гипотез по формулам
P = m : P(B1 ) = 19 ;		P(B2 ) =				6	;	P(B3 ) =	11.

n	36	36							36
Вероятность события А
P(A) = 0,85	19 + 0,76		6		+ 0,71 11 = 0,792.

	36	36						36
По формуле Бейеса	P(B / A) =			P(Bi ) P(A / Bi )					вычисляем ве-

	i					P( A)

роятность того, что работающий безотказно двигатель поставлен третьим заводом-изготовителем:

P(B3 / A) = 0,306 0,71 = 0,274. 0,792

Ответ: Р(B3 /A) = 0,274.

Задача 1.11

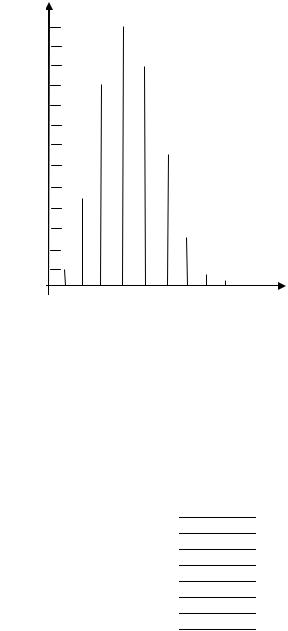
В каждом из 11 независимых испытаний событие А происходит с постоянной вероятностью 0,3. Вычислить все вероятности pk, k = 0, 1, 2, ..., 11, где k – частота события А. Построить график вероятностей pk. Вычислить наивероятнейшую частоту k0 .

Решение:

Задано n = 11, p = 0,3, q = 1 – p = 0,7.

Найти p0, p1, p2,…, p11 и k0 .

Используем		формулу Бернулли pk = Cnk pk qn−k и формулу
pk = n − k +1	p	pk −1, k = 1,...,n.
	q
k

Значение p0 вычисляем по первой из формул, а остальные вероятности pk – по второй.

Для второй формулы вычисляем постоянный множитель и p0: qp = 0,70,3 = 0,428 571 4, p0 = C110 0,30 0,711 = 0,711 = 0,019 773 2.

Результаты вычислений представлены в табл. 1.5. Если вычис-

ления верны, то должно выполняться равенство pk = 1.

k =0

По найденным значениям вероятностей построим их график

(рис. 1.1).

Найдем наивероятнейшую частоту по заданным условиям:

np − q ≤ k0 ≤ np + p,

np − q = 11 0,3 − 0,7 = 3,3 − 0,7 = 2,6; np + p = 3,3 + 0,3 = 3,6 .

0,26Pk

0,24

0,22

0,20

0,18

0,16

0,14

0,12

0,10

0,08

0,06

0,04

0,02

				0	1	2	3	4	5	6	7	8	9	k

		Рис. 1.1. График вероятностей pk к задаче 1.11
	Получим 2,6 ≤ k0 ≤ 3,6 .
	Поскольку k0		– целое число, искомая наивероятнейшая часто-
та k0 = 3 и значение P3					= 0,256 8218 является максимальным.
														Таблица 1.5
										(n − k +1)
k		(n − k +1)			Pk				k	(n − k +1)					Pk
		k										k
0		–	0,019 773 2						6			6/6		0,056 605 6
1		11/1	0,093 216 8						7			5/7		0,017 328 2
2		10/2	0,199 750 3						8			4/8		0,003 713 1
3		9/3	0,256 821 8						9			3/9		0,000 530 4
4		8/4	0,220 133 0						10		2/10			0,000 045 4
5		7/5	0,132 079 8						11		1/11			0,000 001 7
–		–			–				∑			–		0,999 999 4
28

Задача 1.12

В каждом из 700 независимых испытаний событие А происходит с постоянной вероятностью 0,35. Найти вероятность того, что событие А происходит:

а) точно 270 раз; б) меньше, чем 270, и больше, чем 230 раз;

в) больше, чем 270 раз.

Решение:

Учитывая, что количество испытаний n = 700 довольно велико, можно использовать локальную теорему Муавра – Лапласа:

P (k) ≈

ϕ(x)

, ϕ(x) =

e−

, x = k − np

npq

2π

npq

и интегральную теорему Муавра – Лапласа:

Pn (a;b) ≈ Φ(x2 ) − Φ(x1 ),

где

−t

− np

b − np

Φ(x) =

2 dt, x1

npq

, x2

npq

2π −∞

а) задано: n = 700, p = 0,35, k = 270. Найти P700 (270).

Используя локальную теорему Муавра – Лапласа, находим

npq =	700 0,35 0,65 = 159,25 = 12,6;
x =	270 − 700	0,35	=	25,0	= 1,98.
	12,6			12,6

Значение функции ϕ(x) находим из таблицы (прил. 6):

ϕ(1,98) = 0,0562; P700 (270) = 0,056212,6 = 0,004 46;

б) задано: n = 700, p = 0,35, a = 230, b = 270. Найти P700 (230;270) .

Используем интегральную теорему Муавра – Лапласа. Находим:

x = 230 − 700		0,35	= −1,19;	x	2	= 270 − 700	0,35	= 25,0 = 1,98;
1	12,6				2	12,6		12,6
	12,6					12,6		12,6

P700 (230;270) = Ф(1,98) − Ф(−1,19) =

= Ф(1,98) + Ф(1,19) = 0,4761+ 0,3830 = 0,8591.

Значения функции Ф(х) находим из таблицы (прил. 7).

в) задано: n = 700, p =	0,35, a = 270, b				= 700. Найти:
P700 (270;700).
Находим:
npq = 12,6; x = 1,98;	x	2	= 700 − 700	0,35	= 36,1;
1		2	12,6
			12,6

P700 (270;700) = Ф(36,1) − Ф(1,98) = 0,5 − 0,4761= 0,0239.

Задача 1.13

В каждом из 500 независимых испытаний событие А происходит с постоянной вероятностью 0,4. Найти вероятность того, что событие А происходит:

а) точно 220 раз; б) точно 190 раз;

в) меньше, чем 240, и больше, чем 180 раз; г) меньше, чем 235 раз.

Решение:

При решении этой задачи используем теоремы Муавра – Лапласа: локальную в случаяха) иб) и интегральную дляслучаев в) и г).

а) задано: n = 500, p = 0,4, k = 220. Найти P500 (220).

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в папке книги

#
12.11.202316.96 Mб9Теория автоматического управления..pdf
#
12.11.202314.08 Mб3Теория анализа хозяйственной деятельности..pdf
#
20.11.20233.15 Mб140Теория бухгалтерского учета.-1.pdf
#
12.11.20235.23 Mб2Теория бухгалтерского учета..pdf
#
12.11.20233.04 Mб50Теория вероятностей и математическая статистика. Прикладная статистика с использованием MS EXCEL.pdf
#
12.11.2023898.56 Кб7Теория вероятностей и математическая статистика..pdf
#
12.11.202318.27 Mб80Теория вертолета. Кн. 1.pdf
#
12.11.202320.53 Mб20Теория вертолета. Кн. 2.pdf
#
19.11.202329.12 Mб30Теория волочения..pdf
#
12.11.20235.68 Mб10Теория гармонизации опыт когнитивного анализа переводческого пространства..pdf
#
12.11.202321.56 Mб1Теория гомологий. Введение в алгебраическую топологию.pdf