книги / Организация и математическое планирование эксперимента

3.6. Ввести степени переменных аргументов при 1-м коэффи-

циенте b0:

0,0,0.

Ввод подтвердить клавишей Enter.

3.7. Ввести степени переменных аргументов при 2-м коэффи-

циенте b1:

1,0,0.

Ввод подтвердить клавишей Enter.

3.8. Ввести степени переменных аргументов при 3-м коэффи-

циенте b2:

0,1,0.

Ввод подтвердить клавишей Enter.

3.9. Ввести степени переменных аргументов при 4-м коэффи-

циенте b3:

0,0,1.

Ввод подтвердить клавишей Enter.

3.10.Подтвердить подсчет точности аппроксимации (клави-

ша «0», затем Enter).

3.11.Вычислить значения коэффициентов полинома и возникающие при аппроксимации ошибки (клавиша «8», затем Enter).

4. Для получения результатов аппроксимации вывести таблицу результатов (клавиша «1», затем Enter).

Для предела прочности полученные значения коэффициентов следующие:

b0 = 124; b1 = –181; b2 = 178; b3 = 388.

Для вязкости разрушения полученные коэффициенты следующие:

b0 = 10; b1 = –5,75; b2 = 3,1; b3 = 17. 5. Координаты вектора z :

aj = ν1bj(1) + ν2bj(2),

где ν1, ν2 = 1/2.

Например,

a0 = v1b01 + v2b02 = 0,5(124 + 10) = 67,0; a1 = v1b11 + v2b12 = 0,5(181 – 5,75) = 93,38;

21

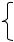
a2 = v1b21 + v2b22 = 0,5(178 + 3,1) = 90,55; a3 = v1b31 + v2b32 = 0,5(388 + 17) = 202,55.

Подставим вычисленные коэффициенты:

z(67,0; –93,38; 90,55; 202,55).

6.Двигаясь по вектору z , выходим на новую область при постоянной концентрации молибдена, так как ее увеличение значительно повышает стоимость стали и понижает характеристики пластичности и вязкости.

В связи с ограниченным масштабом эксперимента следующий этап восхождения выполнен в смежной области. Содержание элементов:

Ni = (0,5±0,5) %; Cr = (4±1) %; Mo = 0,5 %.

7.В представленном примере на 2-м этапе эксперимента содержание молибдена выбрали фиксированным 0,5 %, поэтому достаточно 6 экспериментальных точек (6 уравнений).

8.Строим общую регрессионную модель (аналогично п. 3):

y = b0 + b1CNi + b2CCr + b3CNiCCr + b4CNi2 + b5CCr2.

Исследуем полученные функции на наличие строго локального экстремума:

= 4(–10)(–40) – 3972 = –156 009.

Поскольку определитель отрицателен, найденный локальный экстремум является максимумом.

9. Находим «оптимальные» концентрации элементов:

b1 + b3CCr + 2b4CNi = 0; b2 + b3CNi + 2b5CCr = 0.

22

Решив систему уравнений, получаем следующие оптимальные значения концентраций:

СCr = 3,9 %; CNi = 0,71 %.

10.Экспериментально проверяем свойства «оптимального» состава. Если они не соответствуют расчетным, то продолжаем исследования.

11.Строим регрессионную модель для экспериментальных

значений прочности σв, KIc (табл. 2).

Таблица 2 Сводная таблица экспериментальных значений

12. Строим уравнения регрессии. Для σв

y = b0 + b1CMo + b2CCr + b3CNiCMo + b4CNiCCr +

+ b5CCr2 + b6CMo2 + b7CNi2, F = 1,4;

y = b0 + b1CNi + b2CCr + b3CMo + b4CNiCCr + b5CCrCMo, F = 2,15; (1) y = b0 + b1CNi + b2CCr + b3CMo + b4CMo2 + b5CCr2, F = 1,6.

Следовательно, лучшая модель для вычисления σв соответствует уравнению (1) с максимальным коэффициентом Фишера F и минимальной величиной остаточной дисперсии.

23

Для KIc

y= b0 + b1CMo + b2CCr + b3CNiCCr + b4CNi2 +

+b5CMo2 + b6CCr2 + b7CNiCMo, F = 1,3;

y = b0 + b1CNi + b2CCr + b3CMo + b4CNiCCr + b5CCrCMo, F = 2,25;

y = b0 + b1CNi + b2CCr + b3CMo + b4CMo2 + b5CCr2, F = 3,01. (2)

Следовательно, лучшая модель для вычисления KIc соответствует уравнению (2) с максимальным коэффициентом Фишера и минимальной величиной остаточной дисперсии.

Индивидуальные задания

По предложенным данным (табл. 3) построить регрессионную модель и найти оптимальные составы.

Таблица 3 Исходные данные для выполнения индивидуальных заданий

На 2-м этапе указаны экспериментальные значения свойств в окрестности нового центра эксперимента.

На 3-м этапе указаны экспериментальные значения свойств в точке с «оптимальными» расчетными параметрами.

Контрольные вопросы

1.Сущность оптимизации методом крутого восхождения.

2.Основные идеи двухпараметрического квазикрутого восхождения.

25

3.Основные этапы оптимизации состава этим методом.

4.Критерии адекватности регрессионных моделей и выбора оптимального количества коэффициентов.

Список рекомендуемой литературы

1.Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: учеб. пособие. – 2-е изд., пе-

рераб. и доп. – М.: Высш. шк., 1985. – 327 с.

2.Введение в математическое моделирование: учеб. пособие/ под ред. П.В. Трусова. – М.: Интермет Инжиниринг, 2000. – 336 с.

3.Ясаков А.И. Применение метода квазикрутого восхождения для оптимизации процесса с двумя параметрами выхода // Заводская лаборатория. – 1976. – № 1. – С. 78–79.

26