
Электротехника 1.3 / Laba8_Issledovanie_perekhodnykh_protsessov_v_tsepyakh_pervogo_poryadka_2
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего образования
«Национальный исследовательский Томский политехнический Университет»

Центр цифровых
образовательных технологий
18.03.01 «Химическая технология»
Отчет по лабораторной работе №7
Исследование переходных процессов в цепях первого порядка
по дисциплине:
Электротехника
Исполнитель:
|
|
||||||
студент группы |
2Д02 |
|
Гладыш Полина Валерьевна |
|
24.05.2022 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Руководитель:
|
Каталевская Александра Владимировна |
||||||
преподаватель |
|
|
|
|
|
||
|
|
|
|
|
|
||
Томск – 2022
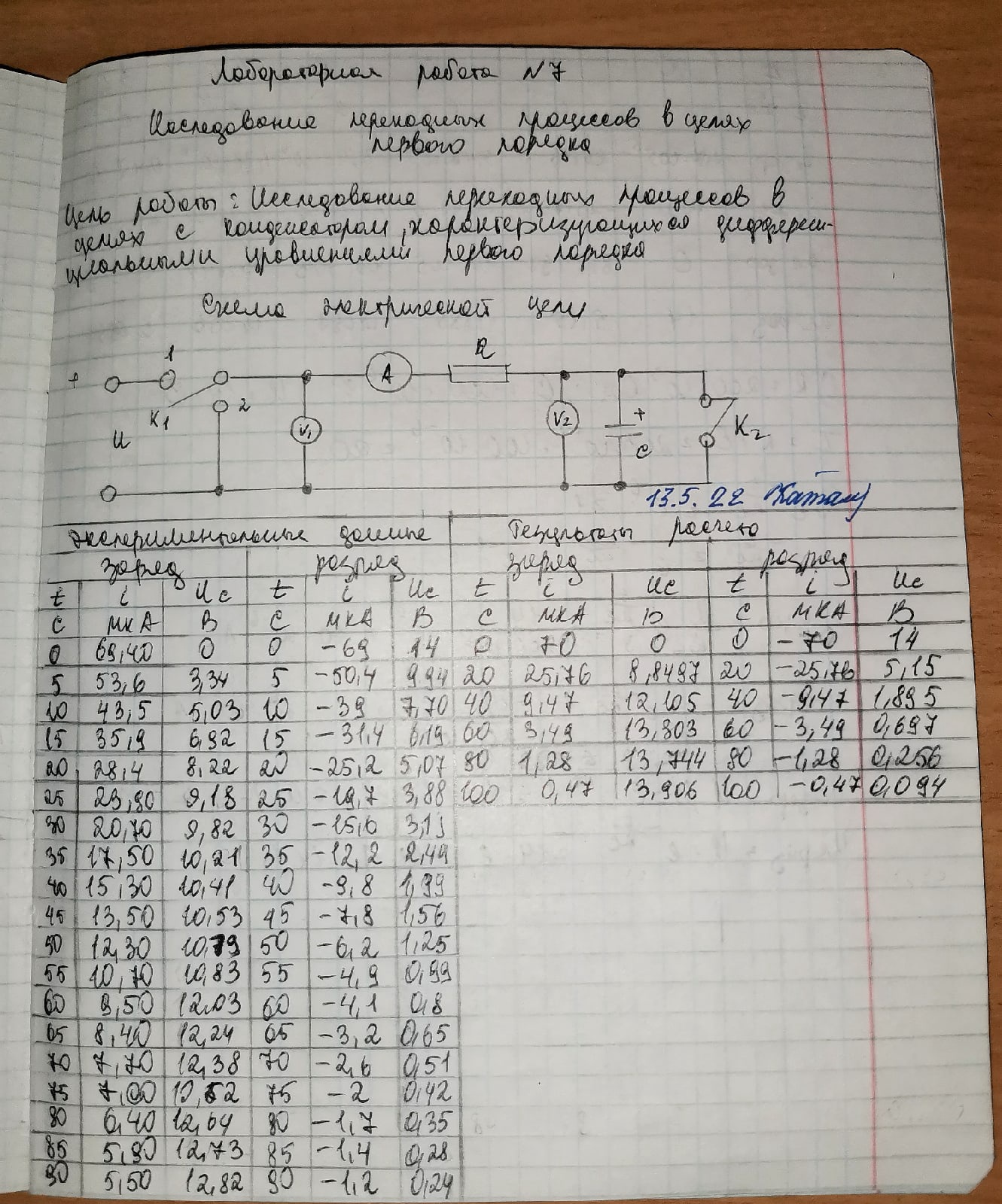


 Константа
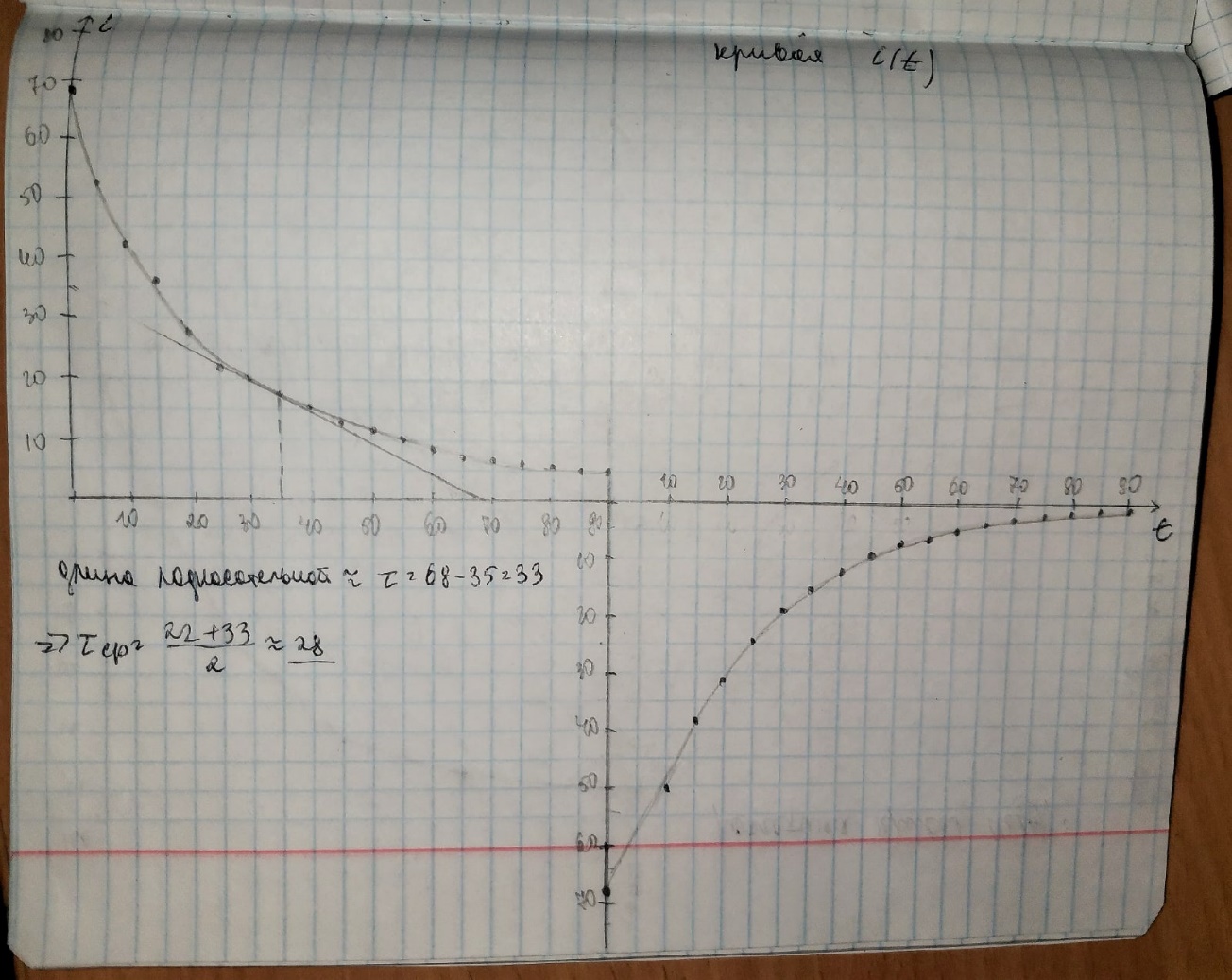
графическим способом по кривым
зависимостей i=f(t),
u=f(t)
равняется длине подкасательной.
Константа
графическим способом по кривым
зависимостей i=f(t),
u=f(t)
равняется длине подкасательной.

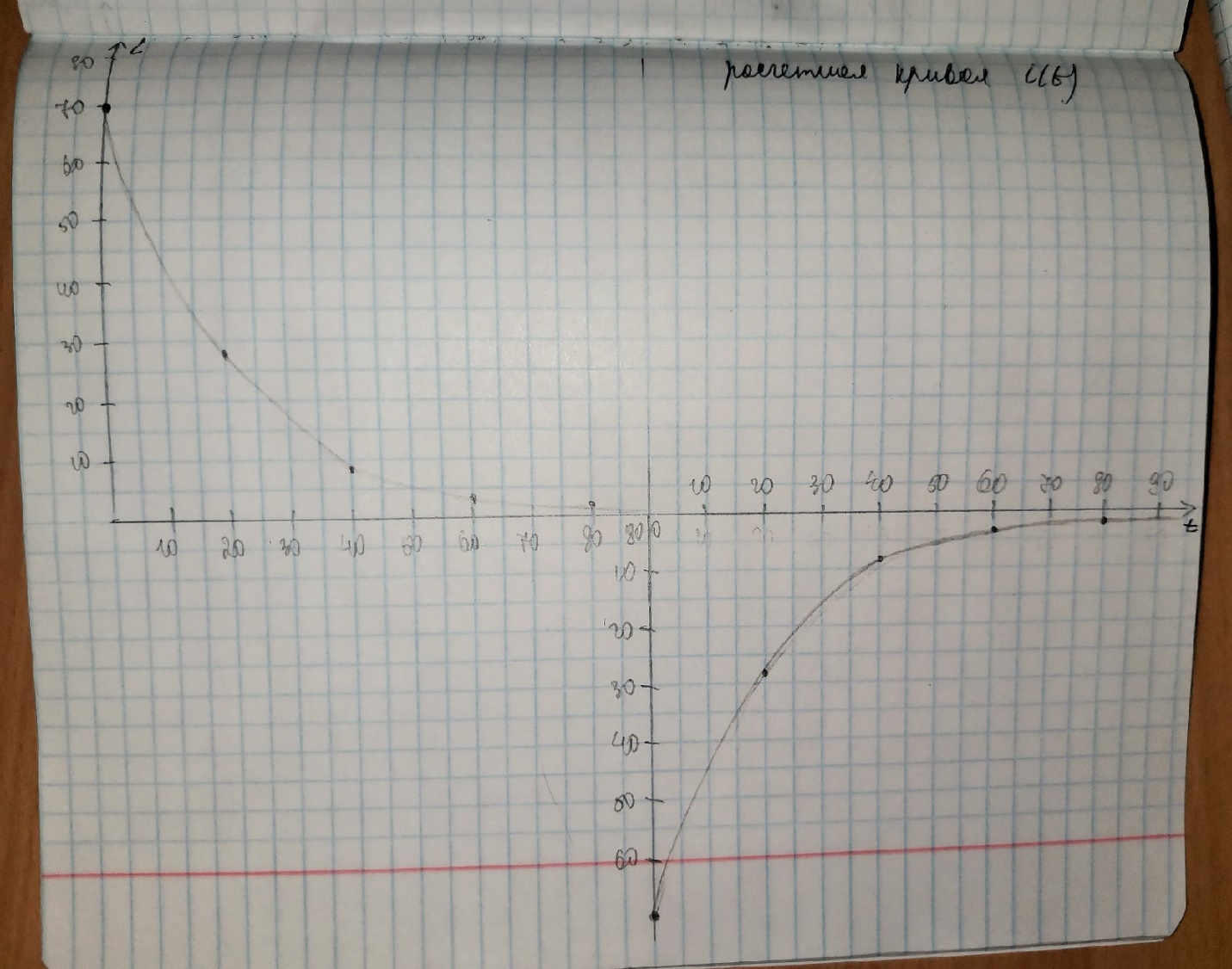
Среднее
значение
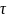 равно 28. Рассчитанное по формуле
равно 28. Рассчитанное по формуле
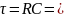 20.
Расхождение значений связано с
погрешностью построения графиков либо
с погрешностью установки.
20.
Расхождение значений связано с
погрешностью построения графиков либо
с погрешностью установки.
Подготовка к работе
В чем причина возникновения переходных процессов?
При всяком изменении режима работы цепи, содержащей хотя бы один накопитель электрической энергии (индуктивность L или емкость C) возникают переходные процессы – процессы перехода от одного установившегося режима к другому.
Сформулировать законы коммутации.
Первый закон коммутации
Ток,
протекающий через индуктивный элемент
L непосредственно до коммутации
![]() ,
равен току, протекающему во время
коммутации, и току через этот же
индуктивный элемент непосредственно
после коммутации
,
равен току, протекающему во время
коммутации, и току через этот же
индуктивный элемент непосредственно
после коммутации
![]() , так как ток в катушке мгновенно
измениться не может:
, так как ток в катушке мгновенно
измениться не может:
![]()
Второй закон коммутации
Напряжение
на емкостном элементе С непосредственно
до коммутации
![]() равно напряжению во время коммутации,
и напряжению на емкостном элементе
непосредственно после коммутации
равно напряжению во время коммутации,
и напряжению на емкостном элементе
непосредственно после коммутации
![]() ,
так как невозможен скачок напряжения
на конденсаторе:
,
так как невозможен скачок напряжения
на конденсаторе:
![]()
Как определить независимые и зависимые начальные условия, принужденные величины?
Независимые условия (начальные значения тока в индуктивности и напряжения на емкости) определяются по законам коммутации и требуют предварительного расчета установившегося режима докоммутационной цепи. Начальные же значения остальных величин (зависимые условия) определяются из уравнений, описывающих состояние послекоммутационной цепи в первый момент после коммутации (t = +0).
Как определить постоянные интегрирования в классическом методе расчета переходных процессов?
Постоянные интегрирования Аk определяются из начальных условий – зависимых и независимых
До коммутации конденсатор не был заряжен, так что по второму закону коммутации 6 uС(+0)=uC(-0)=0. Поэтому

Что такое постоянная времени в цепи первого порядка и как ее определить графически по экспериментальным кривым тока (напряжения)?
Постоянное времени–это величина обратно пропорциональна коэффициента затухания; временная характеристика простой электрической цепи, в которой происходит изменение заряда конденсатора С за счет его разряда через сопротивление R
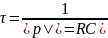
Может быть найдена экспериментально полученный зависимости i(t), как длина подкасательной; графически может определиться как интервал времени на оси t от t=0 до точки пересечения касательной к U.
Чему равна постоянная времени в исследуемой цепи R, C? А в цепи R, L?
τ= RC=200*10^3*100*10^(-6)=20 c
τ=L/Rэ, где Rэ-входное сопротивление исследуемой цепи, измеряем или вычисляем со стороны реактивного элемента.
Вывести формулы (12.2) для расчета тока и напряжения при разряде конденсатора.
Для
переходного процесса разрядки конденсатора
можно записать уравнение
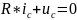 (1)
(1)
Ток
в такой цепи
 (2) подставляем в (1)
(2) подставляем в (1)
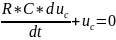 (3)
(3)
Напряжение на конденсаторе найдем по выражению
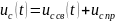
Принужденную
составляющую напряжения
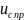 находим из (3) при установившемся режиме
цепи
находим из (3) при установившемся режиме
цепи
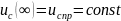 после
коммутации
после
коммутации
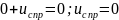
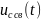 находим,
решая однородное дифференциальное
уравнение
находим,
решая однородное дифференциальное
уравнение
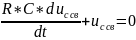 ,
которому соответствует характеристическое
уравнение
,
которому соответствует характеристическое
уравнение
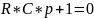
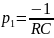
Тогда
свободная составляющая напряжения
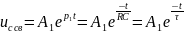 ,
где
,
где
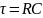 постоянная времени цепи
постоянная времени цепи
Напряжение на конденсаторе в переходном режиме:
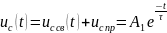
Постоянную
интегрирования
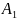 находим
с учетом второго закона коммутации из
начального условия
находим
с учетом второго закона коммутации из
начального условия
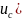
при
t=0
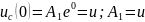
Следовательно
напряжение на конденсаторе в переходном
режиме разряда на резистор R
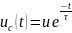
А
ток
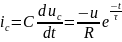
Как рассчитать сопротивление R в цепи рис. 12.2 по результатам измерений в начальный момент времени напряжения при разряде и тока при заряде конденсатора?
В начальный момент времени ток при заряде конденсатора R можно рассчитать R= u/i(0), где i(0) при t=0+, так как в соответствии со вторым законом коммутация напряжение на конденсаторе сохраняет свое значение Uc(0)=0. В начальный момент времени напряжение при разряде конденсатора R можно рассчитать: т.к. напряжение конденсатора в начальный момент не изменится и будет равно u, а т.к. u при заряде, то R=u/i(0).
Вывод: Мы исследовали переходные процессы в цепях с конденсатором, убедились в выполнении законов коммутации. В результате сравнения значений, полученных в результате эксперимента и расчетов, присутствовала погрешность, которую можно объяснить неточностью построений графиков или неточностью приборов. Также наличие погрешности связано с неточностью снятия показаний из-за их быстрой смены, округлением в расчетах.
