Циклические коды

• Циклические коды относятся к групповым кодам, обладающим свойством цикличности.

• Это означает, что цикличная перестановка символов в кодовой комбинации приводит к комбинации, принадлежащей данному коду.

• С алгебраической точки зрения циклическим называется линейный код, который представляет собой конечное множество, замкнутое относительно операций циклического сдвига кодовых векторов, образующих его.

• Все строки порождающей матрицы циклического кода могут быть получены сдвигом влево одной кодовой комбинации с переносом крайнего левого символа в конец комбинации.

Например, для кода 001010 матрица имеет вид:

В теории циклических кодов кодовые комбинации удобно представлять в виде многочленов от фиктивной переменной :

Пример: 100101

Введем операции сложения и умножения:

Операция сложения:

Операция умножения:

учтем ограничения с целью обеспечения замкнутости множества с т.ч. сохранения результата в n-мерном пространстве, используется умножение по модулю , степень равна n:

Здесь - операция взятия остатка, в линейной алгебре в этом случае называют вычетом.

Приведение подобных членов осуществляется суммированием . Что означает эта запись:

Если степень многочлена в числителе меньше n, то остатком от деления на является сам многочлен .

Если нет, то необходимо найти остаток. Остаток и принимается за результат умножения.

Пример1:

Пример2:

⊕	1

Математическое представление операции сдвига кодовой комбинации

Пусть: .

Сдвиг кодовой комбинации влево на разрядов можно записать как:

, где

, если степень не превосходит ,

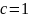- в обратном случае.

для :

Учтем, что

Или, используя терминологию умножения по модулю , имеем:

Где

Рассмотрим задачу выделения циклических кодов из всего множества (кольца) n-символьных кодовых комбинаций. Итак,

1. В множестве существует подмножество , элементы которых связаны свойством цикличности.

2. В теории кодирования доказывается, что подмножества характеризуются тем, что они кратны некоторым многочленам . Данные подмножества называют идеальными, порождаемыми .

3. Если разделить все элементы на , то для элементов идеала остатки от деления будут равны «0», а для всех остальных элементов будут получаться остатки , причем число различных остатков будет определяться видом .

4. Множество можно разложить на смежные классы по идеалу , причем в качестве образующих элементов смежных классов будут выступать .

5. В каждом смежном классе будут собираться те многочлены, которые при делении на , будут давать одинаковый остаток.

Сопоставить с разложением групповых кодов на смежные классы с порождающими элементами в виде векторов ошибок.

Теперь встает вопрос: как выбрать , чтобы он порождал циклический код? Имеем: все элементы циклического кода кратны (индекс убираем), порождающий многочлен длинного кода.

В качестве порождающей матрицы кода, содержащей линейно независимых строк, можно взять и результаты его циклического сдвига.

Старшая степень равна для канонической формы. Учитывая, что математическая модель сдвига есть

то для того, чтобы элементы циклического кода делились на без остатка, необходимо и достаточно, чтобы был делителем ( ).

Имеем: процедура циклического кодирования

На приемной стороне имеем:

прием без искажений,

прием с искажениями.

Таким образом, при декодировании мы должны выполнить определение остатков.

где - операция взятия остатка от деления. Ошибка будет обнаружена, если не делится на без остатка.

Корректирующая способность кода будет тем выше, чем больше разных остатков образуется при делении элементов на .

Наибольшее количество остатков (равное ) от деления дают неприводимые многочлены. Существуют таблицы для разных степеней .

Выбор степени порождающего многочлена:

Условие исправления одиночной ошибки ( :

Для исправления большей кратности ошибок используется правило Хемминга.

Пусть – позволяет исправлять ошибки кратности . Тогда для исправления ошибок кратности :

( увеличивается на 2) – дополнительная проверка на четность.

Выбор подходящего неприводимого многочлена степени :

Часто удобно использовать следующую методику: если , то многочлен равен произведению всех неприводимых многочленов, степени которых являются делителями числа от 1 до .

Пример:

. Один из сомножителей степени может быть взят в качестве . для найденного значения следует выбирать наиболее короткий многочлен, но при этом число его ненулевых членов должно быть не меньше .

Необходимо убедиться, что выбранный многочлен

дает необходимое число разных остатков для реализации исправления нужного числа ошибок.

Пример: (15,11)

Если взять , то остатков будет всего пять, так как входит в разложение не только , но и . Полученный по данной процедуре код будет не систематическим. Для получения систематического разделимого кода используют следующий прием:

1. – безызбыточный код, -символьный.

2. степень

3. Разделим

4. Степень остатка не превосходит