Коды, исправляющие 2-е ошибки

Пример: код (8,2)

Таблицы опознавателей строятся для одиночных ошибок с учетом возможности появления двойных:

Вектор ошибок	Опознаватель
00000001	000001
00000010	000010
00000100	000100
00001000	001000
00010000	001111
00100000	010000
01000000	100000
10000000	110011

В качестве информационных символов можно выбрать и , тогда пров. символы при кодировании:

Представление линейных кодов в матричном виде

В теории кодирования строки и столбцы матриц рассматриваются как вектора кодовых комбинаций. Значения элементов векторов для двоичных кодов – (0,1).

При выполнении матричных операций умножение выполняется обычным способом (0∙0=0, 0∙1=0, 1∙1=1), а сложение производится по модулю 2.

Множество -символьных кодовых комбинаций составляет -мерное линейное векторное пространство. Совокупность разрешенных кодовых комбинаций составляет подмножество -мерного векторного пространства. Множество кодовых комбинаций – векторов линейного кода – можно представить в виде матрицы.

Для кода матрица будет содержать столбцов и строк. При больших и матрица имеет большую размерность и неудобна для проведения операций (ее размер ).

Легко показать, что в этой матрице большинство строк линейно-зависимы. Число линейно-независимых строк равно . Матрица, составленная из линейно-независимых строк – базисная или порождающая матрица кода.

Выберем базисные векторы. Удобнее всего выбрать те, чтобы в матрице ( ) левая часть, соответствующая информационным разрядам составила единичную матрицу, тогда порождающая матрица имеет вид:

где - двоичные символы, каждый ый столбец соответствует одному проверочному разряду и определяет уравнение связи. Подматрица P определяется исходя из уравнений связи для заданного вида подматрицы безызбыточного кода. Данный вид порождающей матрицы называется каноническим. Информационные разряды в порождающей матрице канонического вида представлены единичной подматрицей:

– единичная матрица. Правая часть – матрица - матрица дополнения, соответствует проверочным разрядам, которые вычисляются как:

Пример: код Хэмминга (7,4).

1. Используем уравнение связи вида:

Тогда порождающая матрица имеет вид:

Если хотим сформировать систематический код, то используем уравнения связи вида:

Тогда порождающая матрица имеет вид:

Обозначим вектора-строки порождающей матрицы:

Любая вектор-строка порождающей матрицы , а также любая их линейная комбинация суть разрешенная кодовая комбинация (их число: ), т.е. любую разрешенную кодовую комбинацию можно представить в виде:

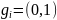
Для того, чтобы определить выходящую (с кодера) кодовую комбинацию необходимо вектор исходного безызбыточного кода

умножить на :

Пример: код (7,4),

Тогда

Имея порождающую матрицу, легко получить проверочную/контрольную матрицу , размером ( . Удобнее всего это сделать для канонической порождающей матрицы. Для нее:

Каждая строка проверочной матрицы соответствует одному проверочному равенству, а коэффициенты задают состав информационных символов, участвующих в проверке. Единица в правой части матрицы указывает номер проверочного разряда.

1. Cигнал не искажен: при умножении на транспонированный вектор неискаженного сигнала получим вектор-столбец, все элементы которого равны нулю.

2. Сигнал искажен: искажение кодовой комбинации приводит к появлению ненулевых . Поэтому вектор-столбец является опознавателем ошибки.

Пример: код (7,4)

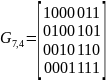
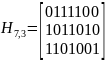
Опознаватели ошибок могут быть найдены умножением на соответствующие векторы-столбцы ошибок, например:

, и т.д.

Видно, что каждый столбец матрицы представляет собой опознаватель ошибок, а номер столбца указывает на номер искаженного символа, если .