Алгоритмы эффективного кодирования

1. Метод Шеннона-Фено

1. Для равновероятных сигналов

	1/4	11
	1/4	10
	1/4	01
	1/4	00

т.е. , при этом бит/ симв.

Для равновероятных сообщений длины кодовых слов одинаковы, код – оптимален.

2. Для неравновероятных сообщений

	0.25	11
	0.25	10
	0.125	011
	0.125	010
	0.0625	0011
	0.0625	0010
	0.0625	0001
	0.0625	0000	бит/ симв.

Код оптимален так как удается разбить на равновероятные блоки.

3. Для неравновероятных сообщений, когда не удается разбить всегда на равновероятные блоки: the same, но

4. Кодирование по блокам. Если не удается разбить на более-менее равновероятные блоки, то можно кодировать сообщения блоками:

	0.89	0
	0.11	1

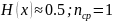
бит/ симв.

А если кодировать блоками:

	0.792	0
	0.098	10
	0.098	110
	0.012	111

бит/ симв.

2. Метод Хафмена

Метод состоит в построении кодового дерева с наиболее длинными ветвями, соответствующими наименее вероятным сигналам. Порядок построения:

• сигналы располагают в порядке убывания вероятности

• два наименее вероятных сигнала объединяются дугами графа

• затем новое ранжирование по вероятности

• опять объединение и т.д.

	0.3	00
	0.2	10
	0.2	11
	0.15	010
	0.1	0110
	0.05	0111

бит

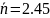симв.

бит/ симв.

Возможность кодирования в условиях шумов

1. Потери информации вызваны наличием шумов

2. Для компенсации потерь информации следует создавать избыточность в передаваемых сообщениях

Пример:

• для непрерывных сигналов – увеличение объема сигнала , например, за счет увеличения и последующей фильтрации

• для дискретных сигналов – введение избыточности в кодовые слова для обеспечения возможности обнаружения и корректировки ошибок.

Условия возможности минимизации потерь при передачи за счет надлежащего кодирования дают теоремы Шеннона.

Теорема 1. Если скорость создания информации на входе шумящего канала меньше его пропускной способности (т.е. ), то существует такой код, при котором вероятность ошибок на приемной стороне будет сколь угодно мала.

Теорема 2. Если , то среди кодов, обеспечивающих сколь угодно малую вероятность ошибки, существуют коды, при которых скорость передачи информации будет сколь угодно близка к скорости создания информации.

Теорема 3. Если , то можно закодировать сообщения таким образом, чтобы потери информации в канале были меньше . При этом не существует способа кодирования, обеспечивающего потери в канале меньше . Заметим, что источника.

Основная теорема Шеннона (Теорема 1) указывает на принципиальную возможность безошибочной передачи информации со скоростью, не превышающей пропускную способность канала. Однако при этом может получится, что для этого необходимо кодировать блоками с длиной кодовых слов .

На практике ИИС не ставится задача безошибочной передачи, но при этом используют коды, позволяющие обнаруживать и исправлять наиболее вероятные ошибки (ошибки ограниченной кратности).

Элементы теории кодирования

Общая квалификация кодов

Способы представления кодов:

• таблицы кодовых комбинаций

• кодовое дерево

• геометрические модели кодов

• алгебраические (алгебра многочленов)

Двоичные двухразрядные:

Троичный двухразрядный:

Двоичный трехразрядный:

Помехоустойчивые кодировки

Основные возможности – теоремы Шеннона.

Идея: кодирование должно осуществляться таким образом, чтобы после воздействия шума на приемной стороне искаженный код оставался ближе к исходному коду, чем к другим возможным посылаемым кодам. Тогда есть возможность обнаружить и даже исправить ошибку в передаче. Такие коды – помехозащищенные, они могут быть корректирующими ошибки или обнаруживающими ошибки.

У большинства помехозащищенных кодов их возможности являются следствием их алгебраической структуры. Алгебраические коды, в отличие о кодов Вагнера, которые корректируют ошибки, исходя из оценки вероятностей ошибок, подразделяются на блоковые и непрерывные коды.

Блоковые коды.

Исходный код – разрядов (символов). Помехоустойчивый код разрядов, при этом - число избыточных символов.

Если , то код равномерный.

Блоковые коды:

• разделимые (состоят из последовательных символов, роль которых заранее известна (информационные или добавочные))

• неразделимые (информационные и проверочные отделить невозможно)

Блоковые коды

На входе кодера – булевы исходные сообщения, закодированные -разрядным цифровым кодом. На выходе кодера – -разрядные коды, причем , т.к. вводим избыточность.

Имеем следующую модель передачи на участке источник-кодер-канал:

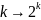кодовых слов

кодовых слов

Число случаев безошибочной передачи - .

Число случаев переходов в другие разрешенные комбинации - .

Число случаев обнаруживаемых ошибочных передач - .

Следовательно, часть обнаруживаемых ошибок от общего числа случаев передач:

Кодовое расстояние

Наличие избыточности приводит к тому, что при приеме мы можем получить неразрешенные комбинации, что позволит обнаружить и откорректировать ошибку. При этом принимаем очевидное предположение, что чем выше кратность (число) ошибок, тем ниже их вероятность.

Для реализации процедур коррекции кодов мы должны принять меру близости полученного кода к исходным. Кодовое расстояние по Хэммингу:

- сумма единиц в коде. Например,

10110001

10101010

---------------

00011011

4

Понятие минимального кодового расстояния.

Декодирование после приема заключается в том, что принятая кодовая комбинация отождествляется с той разрешенной, к которой она наиболее близка ( min). Очевидно, при все кодовые комбинации являются разрешенными и обнаружить ошибку невозможно.

Пример при :

001 001 010 011 100 101 110 111

При 2 одиночные ошибки не могут перевести код в другую разрешенную комбинацию, т.е. ошибка может быть обнаружена.

000 011 101 110 – разрешенная комбинация

001 010 100 111 - запрещенная комбинация

В общем случае, для обнаружения ошибок кратности необходимо:

А теперь рассмотрим условие обнаружения ошибок в коде. При этого сделать нельзя. Возьмем :

Разрешенные комбинации	Запрещенные кодовые комбинации Однократные ошибки
	001
	010
000	100
-------------------------------------------------------------------------
111	011
	101
	110

• При получении одной из трех верхних кодовых комбинаций, мы считаем, что был отправлен код 000 (при условии однократной ошибки).

• При получении одной из трех нижних кодовых комбинаций, мы считаем, что был отправлен код 111.

Т.е. получили возможность исправления.

Графическая интерпретация

Единичные ошибки на окружности , ошибки –кратные на окружности . Для исправления необходимо:

Для задачи обнаружения ошибок кратности и исправления ошибок кратности , требуется:

Геометрическая интерпретация

Оценки необходимой разрядности кода для обеспечения возможности построения помехозащищенного кода.

• Хэмминг:

25+1

• Плоткин: верхняя граница для кодового расстояния для заданных значений :

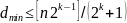
• Разрядность, необходимая для передачи сообщений (000 не используется):

Код Хэмминга код с , позволяющий исправлять все однократные ошибки. Для него количество информационных разрядов:

Уравнение имеет целочисленные решения , которые определяют коды : (3,1); (7,4); (15,11) и т.д.

Граница Варшамова-Гильберта

- определяет существование группового кода, с кодовым расстоянием, не меньшим , и с числом избыточных символов, не превышающем .

(Групповые) блоковые помехозащищенные коды обычно обозначают, как коды, где:

– число информационных разрядов;

– общее число разрядов;

– дополнительные избыточные или поверочные разряды.

Пример: Имеем три сообщения ; для их передачи достаточно , т.к. . Введем избыточность, необходимую для обнаружения одиночных ошибок ( ). Для этого достаточно ввести один дополнительный разряд. Тогда получим:

Самый простой принцип задания дополнительных разрядов и соответственно поверки наличия ошибки при приеме следующий:

То есть:

Тогда на приемной стороне достаточно при получении кодовой комбинации проверить выполнение равенства (проверка на четность):

Вектор ошибок - кодовая комбинация, имеющая «1» в разрядах, подвергшихся искажению, и «0» во всех остальных разрядах. Любую искаженную кодовую комбинацию можно рассматривать как -сумму разрешенной кодовой комбинации и вектора ошибки. Возвратимся к примеру.

Разрешенные комбинации	Искаженные комбинации	Вектор ошибок
	001	001
	010	010
000	100	100
111	011	100
	101	010
	100	011