Передача информации по дискретному каналу

Дискретный канал – это канал, по которому производится передача сигналов, имеющих дискретное множество состояний, т.е. сообщений. При этом дискретной является также сама передача сигналов во времени.

Входной алфавит – алфавит источника сообщений, например , – число сообщений, - буквы алфавита. Для того, чтобы передавать по линиям связи с помощью элементарных сигналов, используют процедуру кодирования, например, используя системы счисления, т.е. , где - элементы кода, а - кодовая комбинация. Элементы символы, например, двоичные. Алфавит кода короче алфавита входного, например, для двоичного кода он состоит из двух символов «0» и «1». Таким образом, для передачи одного сообщения требуется передать пачку символов кода сообщения. Иногда число сообщений не равно длине входного алфавита, если используется начальное кодирование исходных сообщений. например, сообщения:

Входной алфавит:

Для передачи сообщений по дискретному каналу можно использовать разные по форме сигналы, например, бинарные или многоуровневые:

Бинарные сигналы	Дискретный многоуровневый сигнал

В данном разделе мы не будем изучать, как аналоговым сигналом производится и передается импульсный сигнал.

Для передачи дискретных сигналов необходимо:

• задать среднее время передачи одного символа:

– длительность символа

• оценить влияние помех на достоверность передаваемой информации.

Скорость создания информации измеряется в символах в секунду:

, симв./с.= бод

Для двоичного сигнала 1бод=1 бит/сек.

Для многоуровневого сигнала скорость _{бит/сек. бод} – число уровней.

При этом за время по каналу может быть передана информация

Где:

• – информация, передаваемая одним символом.

• - количество информации в битах, созданное источником за время .

• - потери информации за время (в канале).

Тогда реальная скорость передачи информации по дискретному каналу с шумом:

Пропускная способность дискретного канала с шумом:

Максимальная величина выбирается по всем источникам информации.

Как мы видим, понятие пропускной способности применимо как для непрерывных, так и для дискретных каналов. Для непрерывного канала значение пропускной способности соответствует передачи белого шума с ограниченным спектром. В целом, величина пропускной способности определяет возможность передачи сигналов при наличии шумов со сколь угодно малой вероятностью ошибки.

Кодирование информации (сообщений) в дискретном канале.

Введем следующие понятия и обозначения:

– множество входных/ исходных сообщений,

– алфавит входных сообщений,

– алфавит передаваемых/ выходных сообщений,

– множество передаваемых/ выходных кодовых слов над алфавитом выходных сообщений.

Кодирование есть отображение Г: , в частном случае предметом кодирования может быть построение Г₁: .

Пример:

Множество сообщений – слова русского языка, их количество приблизительно равно 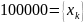. Кодировать слова неудобно из-за их количества. Использует алфавит грамматики русского языка 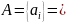а,б,в,г,д,…33 буквы. Тогда Г₁: , т.е. кодировать будем буквы русского алфавита. Для передачи по каналу связи (КС) следует использовать алфавит минимальной длины, например, двоичный, т.е. .

Символы алфавита образуют кодовые слова. В зависимости от условий передачи и принципов кодирования кодовые слова:

• могут иметь различную и непостоянную длину

• различную вероятность появления

• символы в кодовом слове могут быть статистически независимы или коррелированны.

• символы в коде могут иметь различное число значений (для двоичного кода - 2).

Цели и задачи кодирования

1. Обеспечение физических условий передачи сигналов по каналам связи (КС)

2. Обеспечение информационной и энергетической эффективности передачи

3. Повышение помехозащищенности передачи информации

Задача 1. использование алфавита в коде передаваемого сообщения минимальной длины.

Задача 2. построение эффективных кодов (оптимальное кодирование).

Задача 3. построение корректирующих кодов.

Оптимальное кодирование в отсутствии шумов

Оптимальное эффективное кодирование реализует принципы:

1. использование для максимально вероятных сообщений кодов минимальной длины,

2. минимизации средней длины кодовых слов без проверки информации о сигнале.

Имеем:

– кодовое слово, имеет длину символов.

– индивидуальная информация в сообщении .

Считаем символы в слове - статистически независимыми. Идея оптимизации .

Пусть алфавит передачи содержит символов. Считаем значение символов равновероятным. Энтропия одного символа в коде :

Максимальная информация на символ в кодовом слове:

Индивидуальное количество информации в слове :

Оптимальная длина кода для сообщения :

Средняя оптимальная длина слова в кодах:

- энтропия сообщений

Для двоичного кода и

Цель эффективного кодирования – приближение: .

Оценка избыточности/ эффективности кода:

В реальности - целое, тогда

Что не всегда корректно, достаточно и дроби.

Методы оптимального кодирования приводят в общем случае к кодовым словам различной (переменной) длины.

• Использование разделительных символов не всегда эффективно, т.к губит оптимизацию (+1).

• Использование префиксных кодов (ни одна кодовая комбинация не является началом более длинной кодовой комбинации).