
- •Информационная теория сигналов и систем Информационные характеристики сигналов, каналов связи и систем контроля
- •Оценка информационных характеристик сигналов и преобразователей
- •Количество информации в сигнале при наличии помех
- •Передача информации по дискретному каналу
- •Кодирование информации (сообщений) в дискретном канале.
- •Алгоритмы эффективного кодирования
- •Возможность кодирования в условиях шумов
- •Концепция построения помехозащищенного кода.
- •Коды, исправляющие 2-е ошибки
- •Представление линейных кодов в матричном виде
- •Используем уравнение связи вида:
- •Циклические коды
- •Построение систематического кода с помощью генераторного многочлена
Количество информации в сигнале при наличии помех
Информационная модель канала приема/ передачи дискретного сигнала может базироваться на следующих характеристиках:
 -
энтропия множества отправляемых символов
(элементов сообщения)
-
энтропия множества отправляемых символов
(элементов сообщения)
 – энтропия
множества принимаемых символов
– энтропия
множества принимаемых символов
 – энтропия
множества всевозможных пар (
– энтропия
множества всевозможных пар ( )
символов
)
символов
 – энтропия
множества отправляемых символов,
оставшаяся после приема символа
– энтропия
множества отправляемых символов,
оставшаяся после приема символа
 – энтропия
множества принятых символов при условии,
что известен отправленный символ
– энтропия
множества принятых символов при условии,
что известен отправленный символ
- математическое ожидание
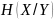 -
математическое ожидание
-
математическое ожидание
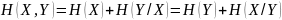
 – количество
информации, полученное при приеме
:
– количество
информации, полученное при приеме
:
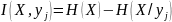
 – среднее
количество информации в объекте
относительно объекта
.
А также:
– среднее
количество информации в объекте
относительно объекта
.
А также:

При этом – среднее количество информации, потерянное из-за воздействия помех.

Напомним:
для дискретного сигнала:
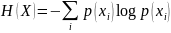

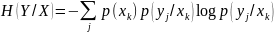
для непрерывного сигнала:


Свойства количества информации


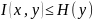


Модели каналов передачи информации
Сообщения в ИИС и системах связи передаются непрерывными или дискретными сигналами (во времени).
Информационные каналы классифицируются:
непрерывные
дискретные
Непрерывные каналы
Моделью
непрерывного канала является линейная
система, характеризуемая: импульсной
переходной функцией
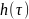 или частотной функцией
или частотной функцией
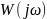 .
.

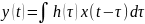

Основной характеристикой непрерывного канала является полоса пропускания.
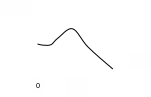
Эффективный частотный диапазон или полоса пропускания:
На практике для передачи сигнала по непрерывному каналу, как правило, используют методы модуляции. В этом случае полоса пропускания канала выбирается исходя из потребности передачи модулированного сигнала.
Передача информации по непрерывному каналу

Причин потерь информации две:
измерение с конечной точностью
шумы
Скорость создания (генерации) информации источником.
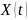 – реализация
случайного процесса
– реализация
случайного процесса
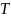 – интервал
наблюдения
– интервал
наблюдения
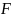 – полоса
частот сигнала (реализации) или спектр
плотности случайного процесса
– полоса
частот сигнала (реализации) или спектр
плотности случайного процесса
Учитывая, что собственная (полная) энтропия непрерывного сигнала стремиться к нулю, будем считать, что процесс получения информации от осуществляется по отсчетам и при этом с конечной погрешностью, определяемой СКО «».
Во
избежание потери информации вследствие
дискретизации, необходимо при формировании
отсчетов обеспечить условия Котельникова
(т.е.
 отсчетов за время
).
отсчетов за время
).
Информация, снимаемая за один отсчет:
 -
-энтропия
сигнала
-
-энтропия
сигнала
За время имеем отсчетов и получаем за счет измерения информацию:
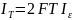
За единицу времени, т.е. скорость генерации информации:
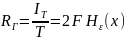
Введем некоторые допущения:
Пусть ошибка измерений нормальна с дисперсией
 ;
;Пусть сигнал на каждом отсчете нормален (белый шум) с дисперсией
 и полосой
.
и полосой
.
Тогда скорость генерации информации:

Скорость передачи и пропускная способность канала
Считаем
полосу пропускания канала достаточной,
т.е.
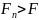 (
– полоса сигнала). Потеря информации в
отсутствии динамических искажений
будет обусловлена только наличием шума
(
– полоса сигнала). Потеря информации в
отсутствии динамических искажений
будет обусловлена только наличием шума
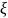 .
.
Считаем также, что измерительное устройство на выходе канала имеет погрешность, значительно меньшую, чем дисперсия приведенного к выходу канала шума .
Далее используем тот же подход к анализу скорости получения информации, что и при анализе скорости ее генерации, т.е. через отсчеты. Только в нашем случае для каждого отсчета:

При этом:

Тогда за время :

Скорость передачи информации:

Пропускная способность канала:

max – по всем возможным законам распределения и .
Предположим корректность аддитивной модели шума:
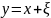
в том числе для любого отсчета, а также распределение по нормальному закону в диапазоне (белые шумы), т.е.:
дисперсия
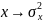
шума

Тогда
 ;
;
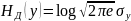

Следовательно,
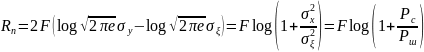
Где
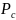 – мощность сигнала (
– мощность сигнала ( ),
),
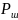 – мощность шума(
– мощность шума(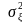 ).
).
