
БДЗ №3 статистика
.docxЗадача 6.6 (вариант 9)
Дана выборка объёма 50:
9,1518; 4,6896; 6,0666; 3,4851; 8,7662; 2,2460; 2,8043; 1,0164; 6,1235; 4,1296; 6,7106; 5,3192; 2,0110; 4,8816; 5,8512; 5,9232; 5,3917; 3,9431; 4,0934; 6,4568; 0,1905; 8,0841; 4,4240; 5,4651; 7,3941; 5,2865; 4,6804; 2,3371; 5,0933; 5,0341; 3,8328; 3,2068; 8,7242; 0,8511; 4,0019; 8,2906; 6,8500; 3,9099; 5,4195; 5,0966; 5,7516; 0,7536; 5,5347; 2,4576; 2,1283; 6,6100; 5,7379; 3,9358; 2,7130; 6,1857
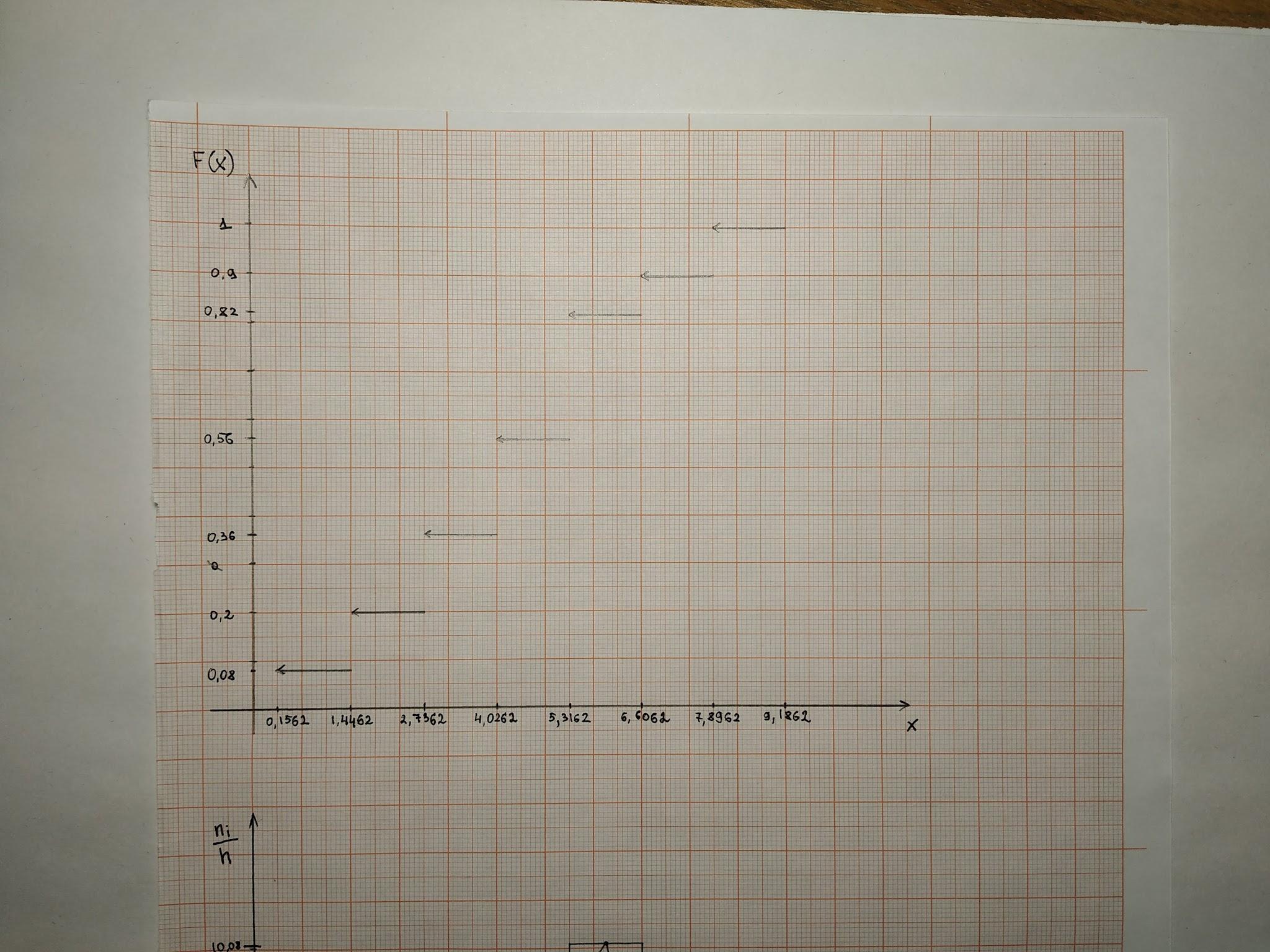
Разобьем отсортированную выборку на семь интервалов с шагом h=1,29:
Начало интервала |
Конец интервала |
Середина интервала |
Частота |
Плотность частоты |
Относительные частоты |
0,1562 |
1,4462 |
0,8012 |
4 |
3,1 |
0,08 |
1,4462 |
2,7362 |
2,0912 |
6 |
4,65 |
0,12 |
2,7362 |
4,0262 |
3,3812 |
8 |
6,2 |
0,16 |
4,0262 |
5,3162 |
4,6712 |
10 |
7,75 |
0,2 |
5,3162 |
6,6062 |
5,9612 |
13 |
10,08 |
0,26 |
6,6062 |
7,8962 |
7,2512 |
4 |
3,1 |
0,08 |
7,8962 |
9,1862 |
8,5412 |
5 |
3,88 |
0,1 |
 На
основе полученных данных построим
гистограмму и полигон частот, а также
эмпирическую функцию:
На
основе полученных данных построим
гистограмму и полигон частот, а также
эмпирическую функцию:
Найдем оценки для математического ожидания, дисперсии, медианы и моды. Рассчитываем по следующим формулам:
![]()
![]()
где n – объем выборки, xi – середина i-го интервала группировки, ni – число элементов выборки в этом интервале; k – число интервалов (разрядов) в группировке.
Мода d оценивается по группировкам данных по следующей формуле:

где at – нижняя граница t-го интервала, содержащего наибольшее число элементов выборки; nt – число элементов выборки в этом интервале; ht – его длина; nt–1 и nt+1 – числа элементов выборки в соседних с ним интервалах.
Для группированной выборки медиана ms оценивается по следующей формуле:
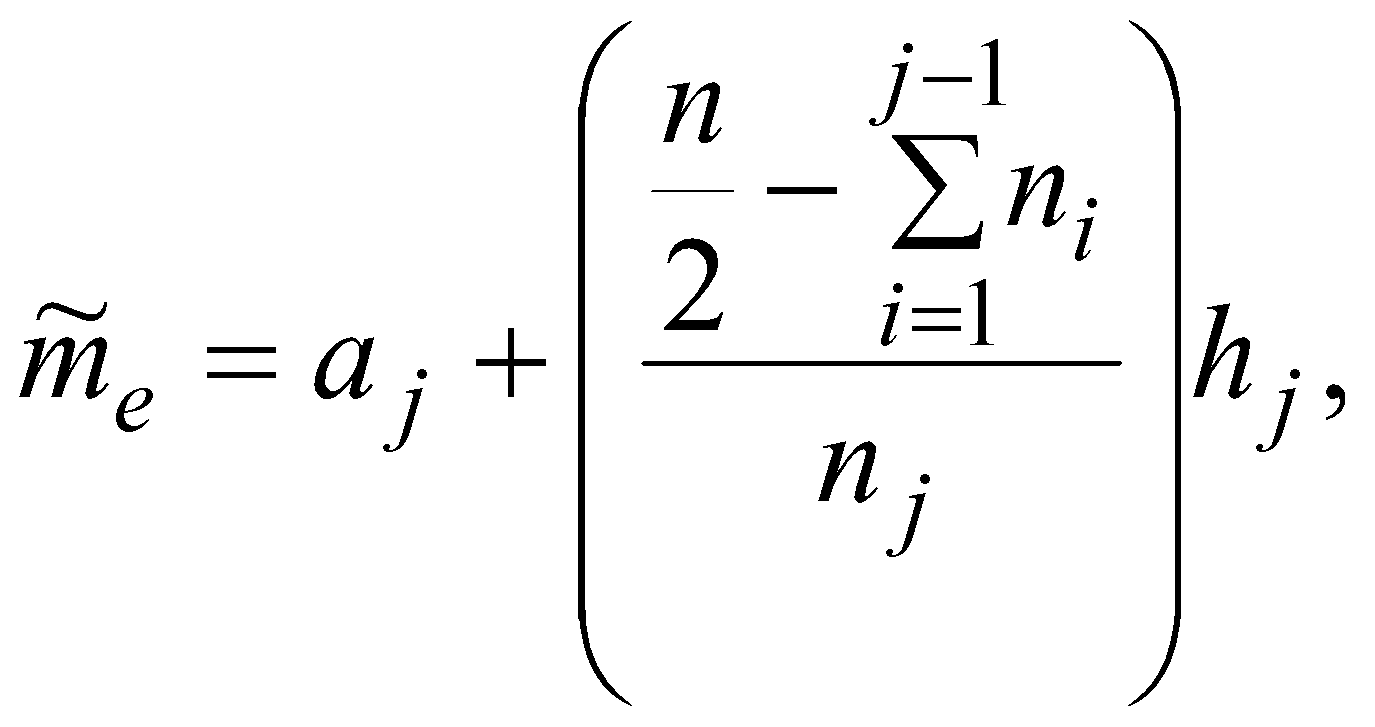
где
аj – нижняя граница j-го
интервала, содержащего середину
вариационного ряда; nj –
число элементов выборки в этом интервале;
![]() – сумма элементов выборки в разрядах,
лежащих слева от этого разряда; hj
– длина jго разряда.
– сумма элементов выборки в разрядах,
лежащих слева от этого разряда; hj
– длина jго разряда.
Для удобства расчетов воспользуемся excel и получим следующие оценки числовых характеристик:
|
|
|
|
медиана |
мода |
4,7744 |
4,71539 |
4,811626 |
2,19354 |
4,9292 |
5,6387 |
Доверительный интервал для математического ожидания находим по формуле:
![]() ,
,
где n=50, S — исправленное среднее квадратичное отклонение, t — коэффициент доверия рассчитывается по таблице значений распределения Стьюдента. Подставляя в формулу ранее вычисленные значения, находим доверительные интервалы для математического ожидания исследуемой генеральной совокупности:
4,15113 < m < 5,39757
Доверительный интервал для дисперсии находим по следующей формуле:
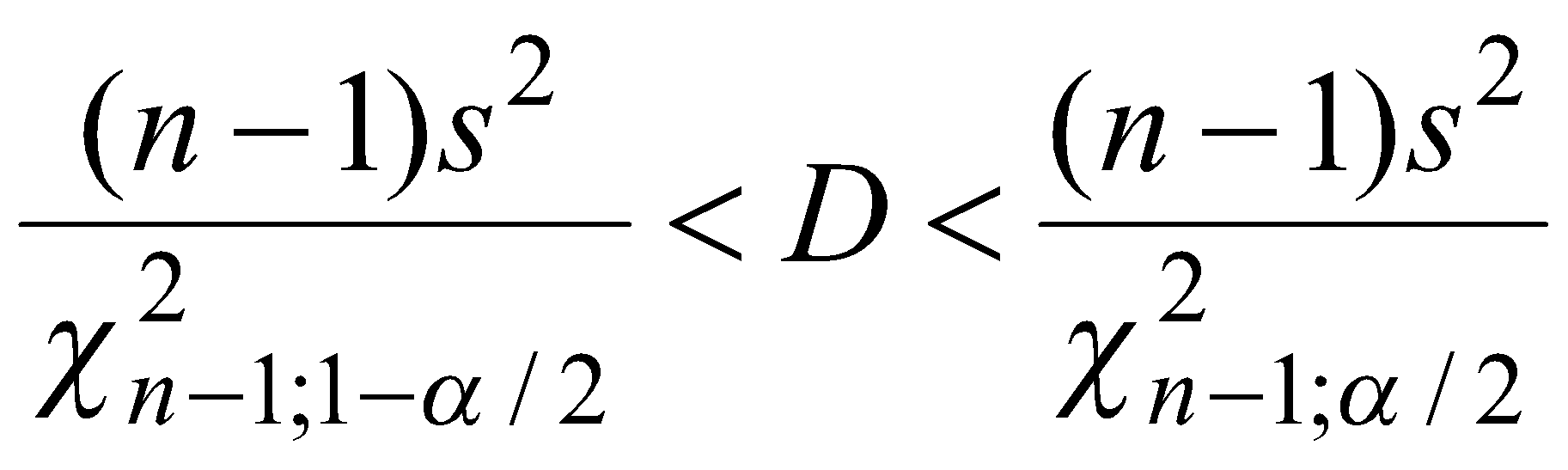
Подставив в формулу необходимые значения, получим следующие доверительные интервалы для дисперсии исследуемой генеральной совокупности:
3,3576 < D < 7,4705
С помощью построенных доверительных интервалов проверим гипотезы:
![]() ,
где
,
где
![]()
![]() ,
где
,
где
![]()
 5,06704 попадает в интервал, гипотезу можно
принять.
5,06704 попадает в интервал, гипотезу можно
принять.
 6,80467 попадает в интервал, гипотезу можно
принять.
6,80467 попадает в интервал, гипотезу можно
принять.
Задача 6.20 (вариант 9)
Последовательность статистической обработки результатов наблюдений двумерной генеральной совокупности проиллюстрируем на примере парной выборки (xi; yi):
X |
Y |
–2,11 |
–6,06 |
9,28 |
1,27 |
5,06 |
9,80 |
12,19 |
10,91 |
3,87 |
5,98 |
4,40 |
6,14 |
5,31 |
6,19 |
4,56 |
1,35 |
8,46 |
5,47 |
5,74 |
5,05 |
4,97 |
1,02 |
7,73 |
4,30 |
12,60 |
19,29 |
–1,05 |
–0,02 |
9,89 |
5,82 |
10,18 |
10,82 |
6,34 |
2,63 |
5,21 |
0,61 |
3,57 |
3,33 |
8,05 |
12,66 |
9,55 |
10,86 |
2,07 |
5,50 |
6,88 |
3,00 |
4,50 |
3,45 |
–2,20 |
–2,45 |
X |
Y |
6,09 |
2,04 |
5,94 |
1,46 |
5,71 |
10,23 |
12,72 |
13,56 |
4,81 |
3,03 |
10,44 |
14,46 |
12,76 |
14,49 |
8,99 |
5,83 |
4,83 |
10,99 |
2,58 |
4,54 |
10,75 |
17,46 |
–1,32 |
4,04 |
–0,44 |
–2,38 |
13,09 |
8,72 |
6,85 |
7,36 |
2,92 |
2,40 |
0,47 |
–2,11 |
6,40 |
9,19 |
–0,25 |
6,51 |
4,76 |
3,38 |
2,81 |
0,23 |
5,97 |
5,78 |
6,97 |
10,42 |
–2,64 |
–5,26 |
8,82 |
4,82 |
Построим для двумерного случайного вектора диаграмму рассеивания. Для этого выберем удобные длины интервалов. Значения первой координаты Х заключены в промежутке [-2,64;13,9], удобно взять интервалы длиной h=2 на промежутке [-2,8;13,2], получив восемь интервалов. Вторая координата У изменяется от -6,06 до 19,29, с размахом 25,35, где ближайшее число кратное 8 — 25,6. Тогда длина интервала h=3,2, удобно взять промежуток [-6,2;19,4]. Получаем такие значения интервалов:
для У |
для Х |
|||
-6,2 |
-3 |
-2,8 |
-0,8 |
|
-3 |
0,2 |
-0,8 |
1,2 |
|
0,2 |
3,4 |
1,2 |
3,2 |
|
3,4 |
6,6 |
3,2 |
5,2 |
|
6,6 |
9,8 |
5,2 |
7,2 |
|
9,8 |
13 |
7,2 |
9,2 |
|
13 |
16,2 |
9,2 |
11,2 |
|
16,2 |
19,4 |
11,2 |
13,2 |
|
Составим диаграмму рассеивания:
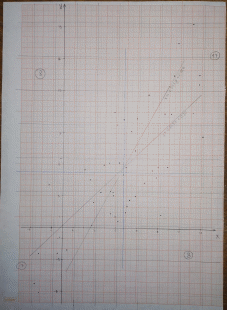
Полученные границы интервалов нанесем на оси диаграммы рассеивания, таким образом, диаграмма разобьется на прямоугольники. Составим таблицу частот опираясь на число точек, попавших в каждый из них:
yi |
|
|||||||
-1,8 |
0,2 |
2,2 |
4,2 |
6,2 |
8,2 |
10,2 |
12,2 |
|
-4,6 |
2 |
|
|
|
|
|
|
|
-1,4 |
2 |
2 |
|
|
|
|
|
|
1,8 |
|
|
2 |
5 |
5 |
|
1 |
|
5 |
1 |
1 |
2 |
3 |
3 |
4 |
1 |
|
8,2 |
|
|
|
1 |
2 |
|
|
1 |
11,4 |
|
|
|
1 |
2 |
1 |
2 |
1 |
14,6 |
|
|
|
|
|
|
1 |
2 |
17,8 |
|
|
|
|
|
|
1 |
1 |
Найдем медианы по каждой координате, используя формулу медианы или найдя среднее арифметическое между 25-м и 26-м значением в отсортированной выборке. Получаем две прямые х=5,725 и у=5,26 и разделим диаграмму на четыре квадранта. О наличии зависимости делаем вывод по числу точек в квадрантах k=8 и m=17. По табл.2 критических значений для определения квадрантной корреляции с достоверностью 0,95 можно утверждать о наличии положительной корреляции между Х и У
Проведем оценку параметров двумерного вектора. Оценим математические ожидания mx и my, дисперсии Dx и Dy случайных величин X и Y, а также коэффициент корреляции ρ.
Числовые характеристики вектора (X, Y)
|
|
|
|
|
|
|
5,6 |
5,512 |
16,53 |
28,57 |
4,066 |
5,345 |
0,719 |
Проведем оценку коэффициентов уравнений линейной регрессии X по Y и Y по X. Формулы, по которым производится оценка коэффициентов уравнений линейной регрессии
![]() ;
;
![]() ,
,
имеют следующий вид:
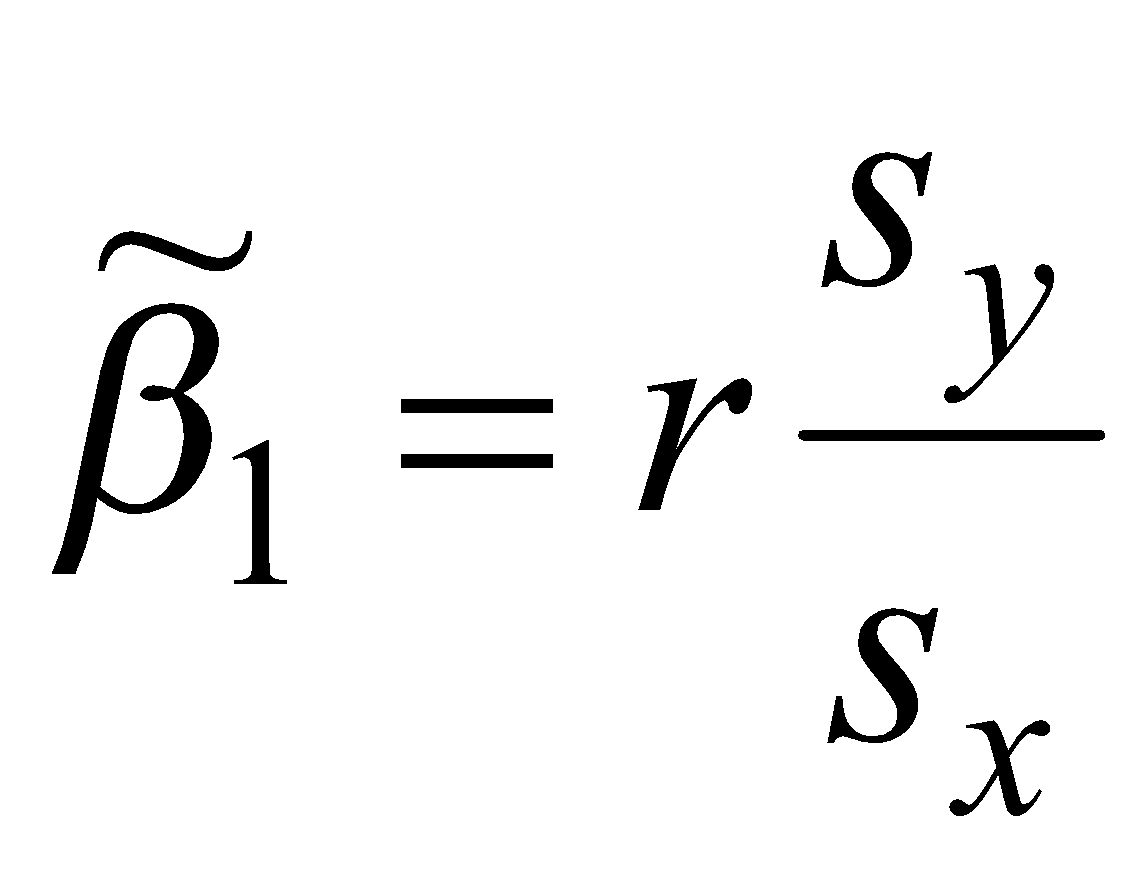 ;
;
![]() ;
;
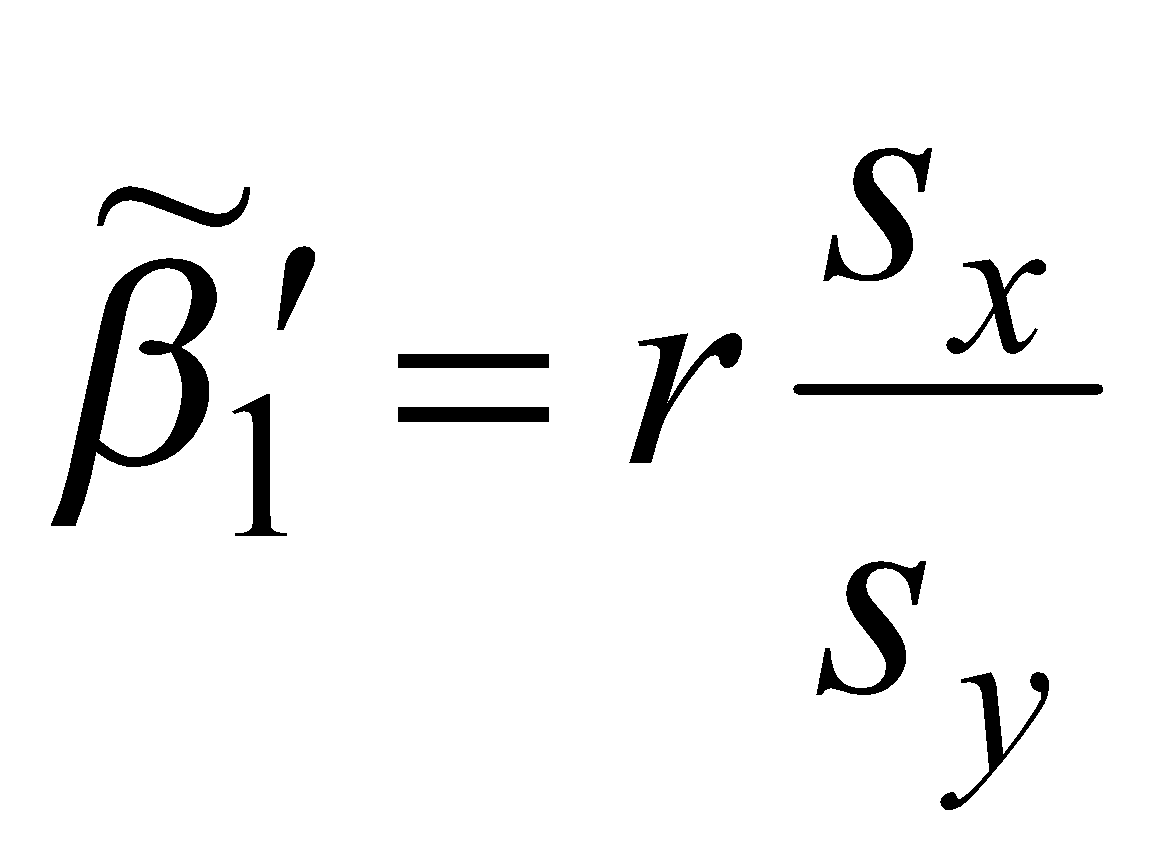 ;
;
![]() .
.
Составим уравнения линейных регрессий, используя числовые характеристики вектора:
У по Х: у=0,22+0,945*х
Х по У: х=2,587+0,547*у
Доверительный интервал для ρ нашли по рисунку 2.3, проведя вертикаль ρ=0,719:
0,48 < ρ < 0,81.
Интервал не содержит нуля, следовательно, с доверительной вероятностью P=1–α=0,95, существует линейная положительная корреляция между X и Y. Исследуемый коэффициент 0,8 лежит в доверительном интервале, гипотезу принимаем.

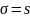
 xi
xi