
дз на зиму КиЦОИ / tspd-06
.pdf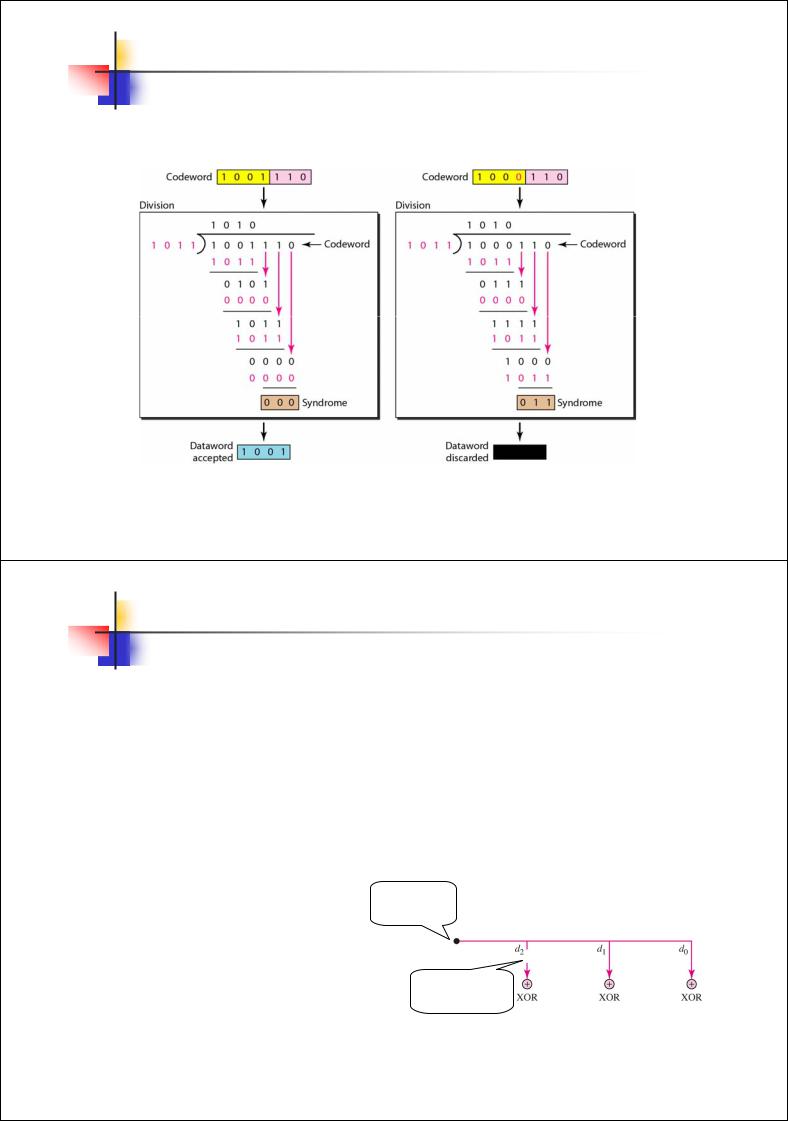
 4. Циклическиекоды
4. Циклическиекоды
Циклическийконтрольсизбыточностью(CRC)
Пример операции деления в декодере CRC :
Процедура деления в декодере такая же как в кодере, но вычисляется синдром
|
Кодовое слово |
|
|
|
|
|
Кодовое слово |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Деление (нет ошибки) |
|
|
|
|
Деление (есть ошибка) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодовое |
|
|
|
Кодовое |
|||
|
|
|
|
слово |
|
|
|
|
|
слово |
|
|
|
Синдром |
|
|
|
Синдром |
|
|
|
|
|
|
|
|
|
|
|
Кодовое слово |
|
|
|||||
|
|
|
|
Кодовое слово |
|
|
||
|
принято |
|
|
отклонено |
|
|
|
|
|
|
Рис. 3.18. Деление в декодере CRC |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Лекция 6. Обнаружение и исправление ошибок |
41 |
|||||
 4. Циклическиекоды
4. Циклическиекоды
РеализациякодаCRC
Аппаратная реализация кода CRC: циклический код легко реализуется благодаря свойствам делителя, кодового слова и остатка
Делитель:
Делитель неоднократно подвергается операции XOR с частью делимого
Делитель имеет n – k + 1 бит, которые либо определены заранее либо все нули, т.е. комбинация делителя фиксирована (в примере 1011 или 0000)
Только n – k бит делителя подвергается операции XOR. Левый бит части делимого в операции не участвует, т.к. результат всегда 0 (в примере только три бит из четырех в действительности используются для операции XOR)
Если левый бит части делимого |
Левый бит |
1 |
=> |
0 |
1 |
1 |
|
1, то комбинация (d2 d1d0 ) = |
делимого |
||||||
011; если левый бит 0 то |
|
|
0 |
=> |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
комбинация (d2 d1d0 ) = 011 |
|
Разрыв: этот |
|
|
|
||
|
|
|
|
|
|||
|
|
бит всегда 0 |
|
|
|
||
|
|
Рис. 3.19. Реализация делителя для кода CRC |
|||||
|
|
|
|
для примера на рис. 3.17 |
|
||
|
|
|
|
||||
Лекция 6. Обнаружение и исправление ошибок |
|
42 |
|||||
 4. Циклическиекоды
4. Циклическиекоды
РеализациякодаCRC
Дополненное нулями информационное слово:
При делении столбиком (пример на рис. 3.17) делимого фиксирована, но позиция делителя на каждом шаге сдвигается вправо (бит слева отбрасывается и бит справа дополняется от делимого)
Для аппаратной реализации удобнее зафиксировать позицию делителя на каждом шаге, а делимое сдвигать влево, при этом нет необходимости хранить в памяти биты делимого
Остаток:
Для хранения промежуточных значений остатка деления можно использовать 1-битные регистры (три регистра для примера на рис. 3.17)
Аппаратное деление:
На первом такте регистры остатка нулевые
На каждом такте (поступление каждого бита делимого) происходит следующее:
–по левому биту остатка определяется делитель (в примере: 011 или 000)
–остальные 2 бита остатка и следующий бит от делимого (всего 3 бита) складываются по модулю 2 (операция XOR) с делителем для получения следующего остатка для следующего такта
Лекция 6. Обнаружение и исправление ошибок |
43 |
|
|
|
|
|
4. Циклическиекоды |
|||||
|
|
|
|
|||||||
|
|
|
|
|
РеализациякодаCRC |
|
|
|
|
Дополненное нулями |
|
|
|
|
|
|
|
|
|
информационное слово |
|
|
|
|
|
|
Такт 1 |
|
||||
|
|
Модель деления для |
|
|
|
|
|
|||
кодера CRC на рис 3.17: |
Такт 2 |
|
||||||||
|
|
|
|
|
||||||
|
|
|
Бит левого регистра |
|
|
|||||
|
|
|
Такт 3 |
|||||||
|
|
|
|
|
аппаратно задает |
|
|
|
|
|
|
|
|
|
|
комбинацию делителя |
|
|
|||
|
|
|
|
|
Такт 4 |
|||||
|
|
|
7 тактов против 4 шага при |
|
|
|
|
|
||
|
|
|
|
|
делении столбиком |
|
|
|||
|
|
|
|
|
Такт 5 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(первые 3 такта – |
|
|
|
|
|
|
|
|
|
|
заполнение регистров) |
Такт 6 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такты 4, 5, 6, 7 логически |
|
|
|||||
|
|
|
Такт 7 |
|||||||
|
|
|
|
|
соответствуют делению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
столбиком |
|
|
|
|
|
|
|
|
Модель имеет 24 регистра |
|
|
|
|
|
||
|
|
|
Финальный остаток |
|||||||
|
|
|
|
|
и 21 операторов XOR |
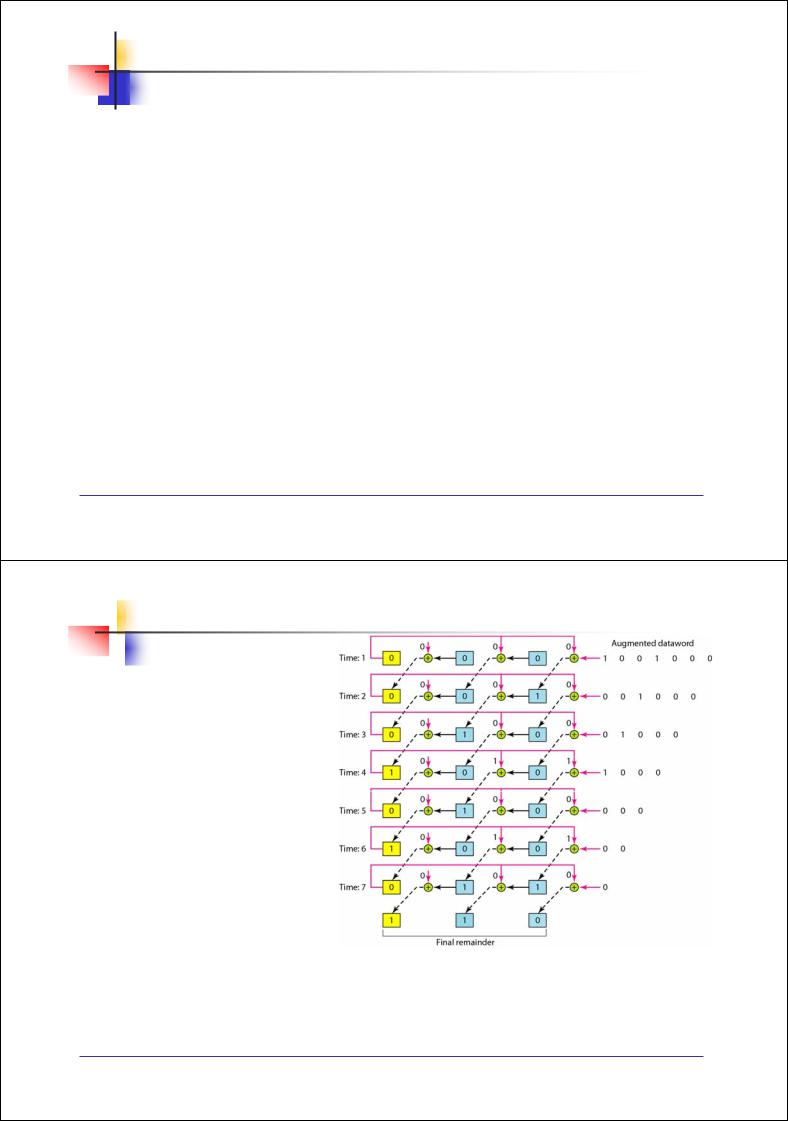
Рис. 3.20. Модель деления в CRC кодере для примера на рис. 3.15 |
||||
Достаточно иметь 3 регистра вместо 24-х, т.к. после операции XOR предыдущий остаток не нужен, т.е. промежуточные значения остатка деления не важны
Достаточно иметь 2 оператора XOR вместо 21, т.к. если один операнд – 0, то результат – значение другого операнда
Лекция 6. Обнаружение и исправление ошибок |
44 |
 4. Циклическиекоды
4. Циклическиекоды
РеализациякодаCRC
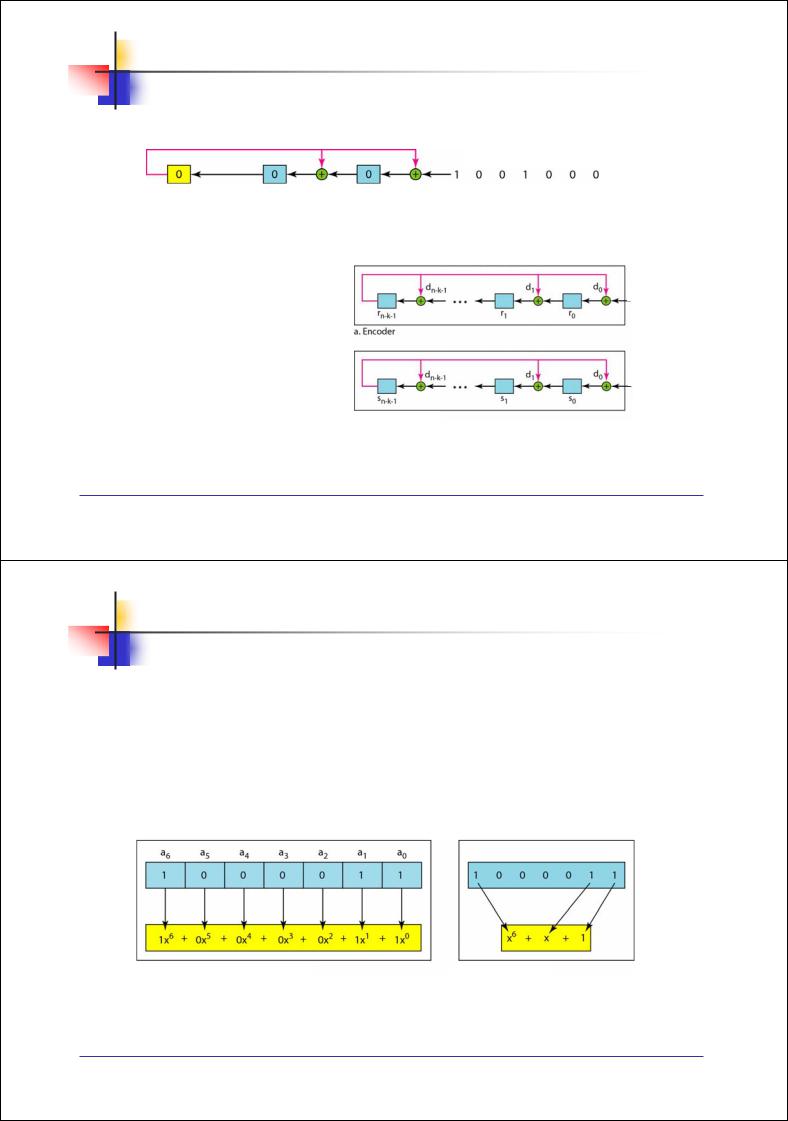
Простой пример реализации CRC кодера (для рис 3.17):
Дополненное нулями информационное слово
Рис. 3.21. Реализация кодера сдвиговым регистром
Общий принцип реализации кодера и декодера CRC:
Количество регистров n – k
Количество операторов XOR вплоть до n – k в зависимости
от комбинации делителя |
|
Кодер |
Если бит делителя 0, то на соответствующей линии разрыв и операция XOR
игнорируется Декодер
Дополненное
информационное
слово
Принимаемое кодовое слово
Рис. 3.22. Принцип реализации кодера и декодера CRC
Лекция 6. Обнаружение и исправление ошибок |
45 |
 4. Циклическиекоды
4. Циклическиекоды
Представлениециклическихкодовввидеполиномастепени
Полиномиальное представление кода: циклический код более удобно представлять в виде полинома некоторой степени, а не элементов 0 и 1
F(x) = a |
n–1 |
xn–1 + a |
xn–2 + … + a |
x2 + a ; |
x – основание, a – элементы |
|
n–2 |
1 |
0 |
|
Комбинация представляется как полином с коэффициентами 0 и 1, степень каждого члена указывает на позицию бита, а коэффициент на его значение
Для краткости все члены с нулевыми коэффициентами удаляются, x1 заменяется на x, x1 на 1
a) Двоичная комбинация и полином |
b) Краткая форма |
Рис. 3.23. Полиномиальное представление двоичного слова
Наибольшая степень в полиномиальном выражении является степенью полинома, например, для выражения x1 + x + 1 степень полинома равна 6
Лекция 6. Обнаружение и исправление ошибок |
46 |

 4. Циклическиекоды
4. Циклическиекоды
Представлениециклическихкодовввидеполиномастепени
Сложение и вычитание полиномов:
Сложение и вычитание полиномов производится путем сложения или вычитания коэффициентов членов с одинаковой степенью
Так как коэффициенты имеют двоичное представление, то операции двоичного сложения и вычитания над ними идентичны и соответствуют операции XOR
Пары идентичных членов в слагаемых удаляются
(x5 + x4 + x2 ) + ( x6 + x4 + x2) = 0 + x5 + x4 + 0 + x2 + 0 + 0
+x6 + 0 + x4 + 0 + x2 + 0 + 0
=x6 + x5
Умножение или деление членов полинома:
При умножении полиномов складываются степени членов x3 × x4 = x7
При делении полиномов вычитаются степени членов x5/x2 = x3
Лекция 6. Обнаружение и исправление ошибок |
47 |
 4. Циклическиекоды
4. Циклическиекоды
Представлениециклическихкодовввидеполиномастепени
Умножение двух полиномов :
Умножение двух полиномов производится по правилу перемножения степенных функций, но коэффициенты складываются по модулю 2
Каждый член первого полинома умножается на все члены второго
(x5 + x3 + x2 + x)( x2 + x + 1)
=x7 + x6 + x5 + x5 + x4 + x3 + x4 + x3 + x2 + x3 + x2 + x
=x7 + x6 + x3 + x
Операция сдвига:
При сдвиге влево добавляются нулевые элементы справа, при сдвиге вправо удаляются биты справа
Сдвиг влево выполняется умножением каждого члена полинома на xm, где m – количество сдвигаемых бит
Сдвиг вправо выполняется делением каждого члена полинома на xm
Сдвиг влево на 3 бита: |
10011 => 10011000 |
x4 + x + 1 |
=> |
x7 + x4 + x3 |
Сдвиг вправо на 3 бита: |
10011 => 10 |
x4 + x + 1 |
=> |
x |
При операции деления в кодере делимое создается путем сдвига влево ( на 3 бит)
Лекция 6. Обнаружение и исправление ошибок |
48 |
 4. Циклическиекоды
4. Циклическиекоды
Представлениециклическихкодовввидеполиномастепени
Кодер циклического кода с использованием полиномов:
Информационное слово
Деление (нет ошибки)
Делитель
Делимое
Остаток
Кодовое слово
Информационное слово Остаток
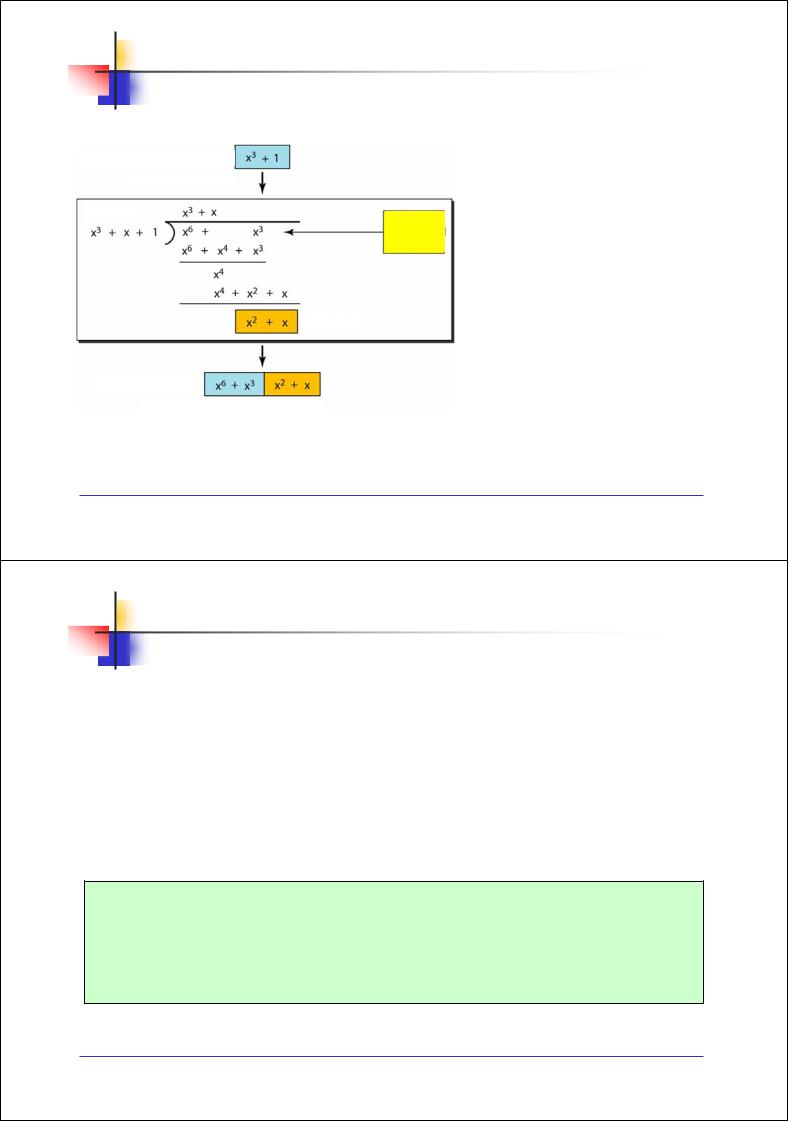
Рис. 3.24. Деление CRC с использованием полиномов
Деление продолжается до тех пор, пока степень остатка будет меньше степени делителя
Информационное слово 1001 представляется как x3 + 1, делитель 1011 представляется как x3 + x + 1
Для нахождения делимого инф. слово сдвигается влево на 3 бита (умнож. на x3), результат x6 + x3
Первый член делимого, x6, делится на первый член делителя, x3. Результат – первый член частного x3, который затем умнож. на делитель (x3 + x + 1)
Результат (x6 + x4 + x3) ) вычитается из делимого и получается x4 со степенью, большей чем у делителя
Лекция 6. Обнаружение и исправление ошибок |
49 |
 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Анализ возможностей циклического кода с помощью полиномов:
С помощью полиномов f(x) с двоичными коэффициентами обозначим следующие функции:
d(x) – информационное слово; |
с(x) – кодовое слово; s(x) – синдром; |
g(x) – генератор (делитель); |
e(x) – ошибка; |
В циклических кодах если один или более бит искажены, то синдром отличен от нуля, синдром нулевой в случае отсутствия ошибок либо если ошибки не обнаружены
Для циклического кода
1)Если s(x) ≠ 0, один или более бит искажены
2)Если s(x) = 0, либо
а) искаженных бит нет, либо б) какие-то биты искажены, но ошибки не обнаружены декодером
Лекция 6. Обнаружение и исправление ошибок |
50 |

 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Критерии выбора генератора:
Принятое слово можно представить в виде суммы: с(x) + e(x)
Для получения синдрома приемник делит принимаемое кодовое слово на g(x):
Принимаемоеслово |
= |
c(x) |
+ |
e(x) |
|
g(x) |
|
|
|
||
g(x) |
g(x) |
||||
Первый член правой части уравнения не имеет остатка. Следовательно, синдром
– это остаток второго члена. Если синдром нулевой, то либо e(x) = 0 либо e(x) делится на g(x) (ошибки при этом не обнаруживаются)
В циклическом коде ошибки, комбинация e(x) которых делится на g(x), не обнаруживаются
Генератор g(x) для обнаружения одиночной ошибки:
Одиночную ошибку можно представить в виде e(x) = xi, где i – позиция бита
При обнаружении одиночной ошибки xi не делится на g(x), остаток не нулевой
Если g(x) имеет по крайней мере два члена и коэффициент x0 ≠ 0 (крайний правый бит = 1), то e(x) не может делиться на g(x) без остатка
Лекция 6. Обнаружение и исправление ошибок |
51 |
 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Если генератор g(x) имеет более чем один член и и коэффициент x0 = 1, то обнаруживаются все одиночные ошибки
Пример15
Который из следующих генераторов g(x) гарантирует обнаружение любой одиночной ошибки? Какие ошибки для этих случаев не обнаруживаются?
1.x + 1
2.x3
3.1
Решение
1.Ни одна из комбинаций xi не может делится на x + 1. Т.е. xi/(x + 1) всегда имеет остаток. Следовательно, синдром не равен нулю и все одиночные ошибки обнаруживаются
2.Если i ≥ 3, то xi делится на g(x). Т.е.остаток от xi/x3 нулевой и приемник ложно решает, что ошибка есть. Обнаруживаются лишь одиночные ошибки на позициях 1…3, ошибки на позициях 4 и выше не обнаруживаются
3.Любая комбинация xi делится на g(x) без остатка и ни одна одиночная ошибка не может быть обнаружена
Лекция 6. Обнаружение и исправление ошибок |
52 |
 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
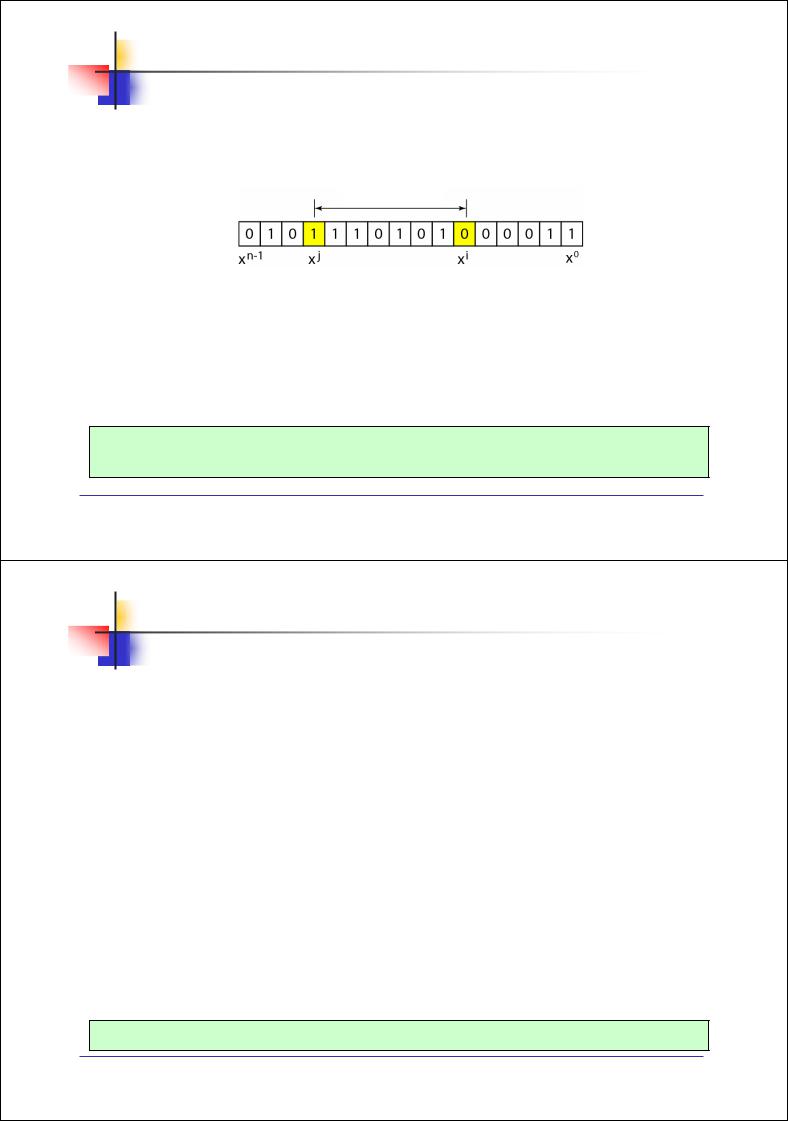
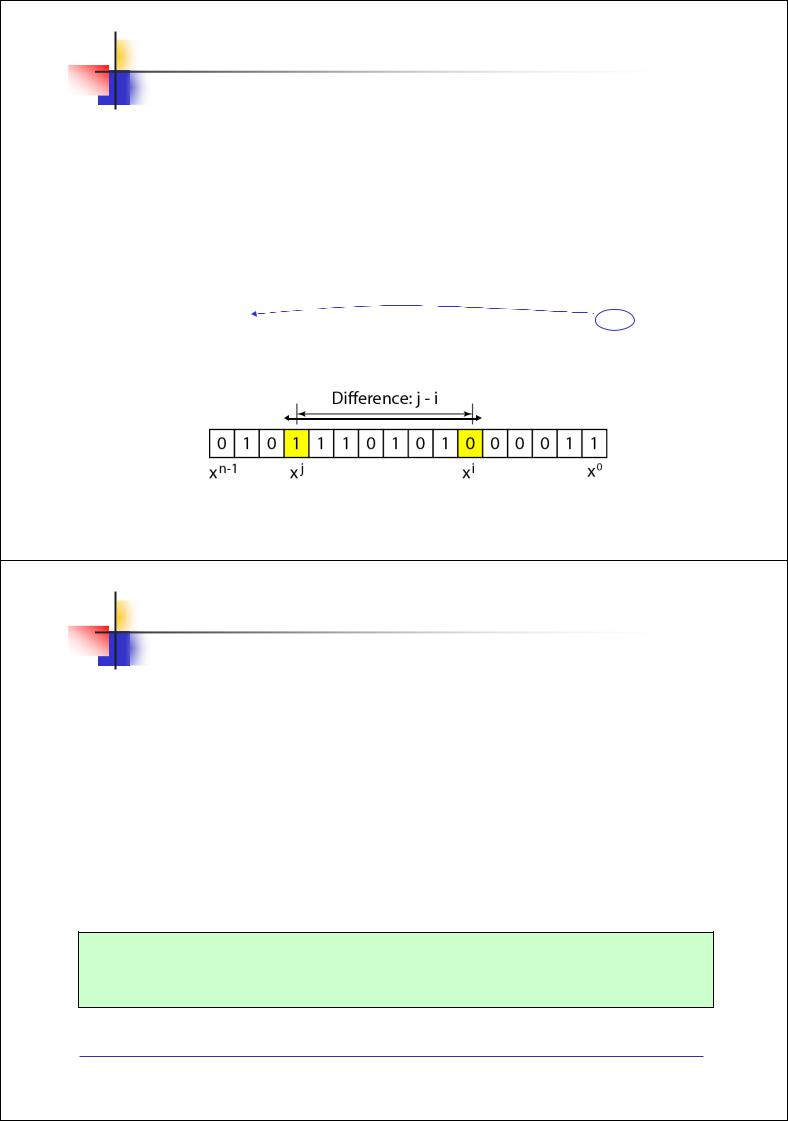
Генератор g(x) для обнаружения двух изолированных одиночных ошибок:
Представим две изолированные одиночные ошибки в виде : e(x) = xj + xi, где i и j – определяют позиции ошибок, а разница j – i есть расстояние между
ошибками |
Разность i – j |
|
Рис. 3.25. Две изолированные одиночные ошибки
Комбинацию двух ошибок можно записать в виде: e(x) = xi(xj–i + 1)
Если g(x) имеет более одного члена и один из них x0, то xi не делится на g(x)
Ошибка e(x) будет делиться на g(x), только если xj–i + 1 будет делиться на g(x), иначе говоря, для обнаружения двух одиночных ошибок xt + 1 не должен делиться на g(x), где t = j – i – разница в пределах от 0 до n – 1
Любые две изолированные одиночные ошибки могут быть обнаружены если выражение xt + 1 (t в пределах от 2 до n – 1) не делится на g(x)
Лекция 6. Обнаружение и исправление ошибок |
53 |
 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Пример16
Который из следующих генераторов g(x) гарантирует обнаружение любых двух изолированных одиночных ошибок?
1.x + 1
2.x4 + 1
3.x7 + x6 +1
Решение
1.Любая пара рядом расположенных одиночных ошибок (j – i =1) не может быть обнаружена, т.к. в этом случае x1 + 1 делится на x + 1 без остатка
2.Любые две ошибки, расположенные на расстоянии четыре позиции (j – i =4), не обнаруживаются, т.к. в этом случае xj– i+ 1 делится на x4 + 1 без остатка
3.Две изолированные одиночные ошибки обнаруживаются при любом их расположении
Генератор g(x) для обнаружения нечетного количества ошибок:
Любое количество нечетных ошибок обнаруживается любым генератором g(x), имеющим множитель x + 1. Например, генератор x4 + x2 + x +1 может быть представлен как произведение двух полиномов: x +1 и x3 + x2 + 1
Нечетное количество ошибок обнаруживается генератором с множителем x + 1
Лекция 6. Обнаружение и исправление ошибок |
54 |
 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Генератор g(x) для обнаружения пакетных ошибок:
Наибольшее значение имеют пакетные ошибки, которые могут быть представлены в форме: e(x) = (xj + … + xi), количество членов в выражении – два и более
Комбинацию всех ошибок в пакете можно записать в виде: e(x) = xi(xj–i + … + 1)
Ошибки обнаруживаются в том случае, если выражение xj–i + … + 1 не делится на генератор g(x), т.е. остаток от (xj–i + … + 1)/(xr + … + 1) не нулевой, где выражение (xr + … + 1) – генератор и r – его макс. степень (избыточность)
Рассмотрим три случая:
1.При любых j – i < r, остаток всегда не нулевой. Запишем j – i = L – 1, где L – длина ошибки. Следовательно, L – 1 < r или L < r + 1 или L ≤ r. Это означает, что все пакетные ошибки, длиной меньшей или равной числу проверочных бит, будут обнаружены.
|
|
Длина пакетной ошибки L |
|
|
|
|
||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
Рис. 3.26. Пакетная ошибка |
|
|||||||
Лекция 6. Обнаружение и исправление ошибок |
55 |
|||||||||
 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Генератор g(x) для обнаружения пакетных ошибок:
2.В некоторых редких случаях, если j – i = r или L = r + 1 синдром оказывается нулевой и пакетная ошибка не обнаруживается. В этом случае вероятность не обнаружения пакетной ошибки длиной r + 1 равна 0,5r–1.
Например, g(x) = x14 + x3 +1 , где r = 14, тогда пакетная ошибка длиной L = 15 может быть пропущена с вероятностью 0,514–1, что примерно 1/10000 (0,000122)
3.В некоторых редких случаях, если j – i > r или L > r + 1 синдром оказывается нулевой и пакетная ошибка не обнаруживается. В этом случае вероятность не обнаружения пакетной ошибки длиной более чем r + 1 равна 0,5r. Например, g(x) = x14 + x3 +1 , где r = 14, тогда пакетная ошибка длиной L > 15 может быть пропущена с вероятностью 0,514 , что примерно 1/16000 (0,000061)
Все пакетные ошибки длиной L ≤ r обнаруживаются
Все пакетные ошибки длиной L = r + 1 обнаруживаются с вероятностью 1 – 0,5r–1
Все пакетные ошибки длиной L > r + 1 обнаруживаются с вероятностью 1 – 0,5r
Лекция 6. Обнаружение и исправление ошибок |
56 |

 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Пример17
Который из следующих генераторов g(x) гарантирует обнаружение пакетных ошибок различной длины?
1.x6 + 1
2.x18 + x7 + x + 1
3.x32 + x23 + x7 + 1
Решение
1.Такой генератор способен обнаружить все пакетные ошибки длиной L ≤ 6 бит; пакетная ошибка длиной L = 7 бит будет пропущена с вероятностью 0,03; пакетная ошибка длиной L ≥ 8 бит будет пропущена с вероятностью 0,016.
2.Такой генератор способен обнаружить все пакетные ошибки длиной L ≤ 18 бит; пакетная ошибка длиной L = 19 бит будет пропущена с вероятностью 8·10–6; пакетная ошибка длиной 20 и более бит будет пропущена с вероятностью 4·10–6.
3.Такой генератор способен обнаружить все пакетные ошибки длиной L ≤ 32 бит; пакетная ошибка длиной L = 33 бит будет пропущена с вероятностью 5·10–10; пакетная ошибка длиной 34 и более бит будет пропущена с вероятностью 3·10–10.
Лекция 6. Обнаружение и исправление ошибок |
57 |
 4. Циклическиекоды
4. Циклическиекоды
Анализциклическогокода
Критерии по выбору генератора:
Полином генератора (образующий полином) должен удовлетворять следующим условиям:
1.Должен иметь по крайней мере два члена
2.Коэффициент члена x0 должен быть равен 1
3.Не должен делиться на xt + 1, для t от 2 до n – 1
4.Должен иметь множитель x + 1
Стандартные образующие полиномы:
|
Код |
Полином |
Применение |
||
|
CRC-8 |
x8 + x2 + x + 1 |
ATM заголовок |
||
|
CRC-10 |
x10 |
+ x9 + x5 + x4 + x2 + 1 |
ATM AAL |
|
|
CRC-16 |
x16 |
+ x12 |
+ x5 + 1 |
HDLC |
|
CRC-32 |
x32 |
+ x26 |
+ x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + |
Локальные |
|
|
x4 + x2 + x + 1 |
сети LAN |
||
|
|
|
|
|
|
|
|
|
|
Лекция 6. Обнаружение и исправление ошибок |
58 |
