3.7. Двойственный симплекс-метод

Двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в форме основной задачи, для которой среди векторов P_j, составленных из коэффициентов при неизвестных в системе уравнений, имеетсяmединичных. Вместе с тем двойственный симплекс–метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Такую задачу и рассмотрим теперь, предварительно предположив, что единичными являются векторP₁,P₂,…,P_m ,т. е. рассмотрим задачу, состоящую в определении максимального значения функции

F=c₁x₁+c₂x₂+…+c_nx_n , (1)

при условиях

x₁P₁+x₂P₂+…+x_mP_m+x_m+1P_m+1+…+x_nP_n=P₀ , (2)

x_j ≥ 0,j=1..n (3)

где

и среди чисел b_i , i=1..mимеются отрицательные.

В данном случае X=(b₁;b₂;…;b_m;0;…;0)есть решение системы линейных уравнений (2). Однако это решение не является планом задачи (1) – (3), так как среди его компонент имеются отрицательные числа.

Поскольку векторы P₁,P₂,…,P_m единичные, каждый из векторовP_j, j=1..nможно представить в виде линейной комбинации данных векторов, причем коэффициентами разложения векторовP_jпо векторамP₁,P₂,…,P_mслужат числаx_ij=a_ij, i=1..m,j=1..nТаким образом, можно найти

Определение 1.

Решение X=(b₁;b₂;…;b_m;0;…;0) системы линейных уравнений (2), определяемое базисомP₁,P₂,…,P_m, называется псевдопланом задачи (1) – (3), еслиΔ_j ≥ 0 для любогоj=1..n

Теорема 1.

Если в псевдоплане X=(b₁;b₂;…;b_m;0;…;0), определяемом базисомP₁,P₂,…,P_m, есть хотя бы одно отрицательное числоb_i < 0такое, что всеa_ij ≥ 0, j=1..n, то задача (1) – (3) вообще не имеет планов.

Теорема 2.

Если в псевдоплане X=(b₁;b₂;…;b_m;0;…;0), определяемом базисомP₁,P₂,…,P_m, имеются отрицательные числаb_i < 0такие, что для любого из них существуют числаa_ij < 0, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (1) – (3) не уменьшится.

Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.

Итак, продолжим рассмотрение задачи (1) – (3). Пусть X=(b₁;b₂;…;b_m;0;…;0) – псевдоплан этой задачи. На основе исходных данных составляют симплекс-таблицу (табл. 1), в которой некоторые элементы столбца вектораP₀являются отрицательными числами. Если таких чисел нет, то в симплекс-таблице записан оптимальный план задачи (1) – (3), поскольку, по предположению, всеΔ_j ≥ 0. Поэтому для определения оптимального плана задачи при условии, что он существует, следует произвести упорядоченный переход от одной симплекс–таблицы к другой до тех пор, пока из столбца вектораP₀ не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными все элементы(т +1)–йстроки, т.е.z_j – с_j ≥ 0 для любогоj,j=1..n.

Таким образом, после составления симплекс-таблицы проверяют, имеются ли в столбце вектора P₀ отрицательные числа. Если их нет, то найден оптимальный план исходной задачи. Если же они имеются (что мы и предполагаем), то выбирают наибольшее по абсолютной величине отрицательное число. В том случае, когда таких чисел несколько, берут какое–нибудь одно из них: пусть это числоb_l.Выбор этого числа определяет вектор, исключаемый из базиса, т. е. в данном случае из базиса выводится векторP_l.Чтобы определить, какой вектор следует ввести в базис, находимmin (-Δ_j / a_lj), гдеa_lj < 0.

Пусть это минимальное значение принимается приj=r, тогда в базис вводят векторP_r.Числоa_lrявляется разрешающим элементов. Переход к новой симплекс–таблице производят по обычным правилам симплексного метода. Итерационный процесс продолжают до тех пор, пока в столбце вектораP₀не будет больше отрицательных чисел. При этом находят оптимальный план исходной задачи, а следовательно, и двойственной. Если на некотором шаге окажется, что вi–йстроке симплекс–таблицы (табл. 1) в столбце вектораP₀стоит отрицательное числоb_i, а среди остальных элементов этой строки нет отрицательных, то исходная задача не имеет решения.

Таким образом, отыскание решения задачи (1) – (3) двойственным симплекс-методом включает следующие этапы:

1. Находят псевдоплан задачи.

2. Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.

3. Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца вектора P₀и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов(m+1)–йстроки к соответствующим отрицательным элементам разрешающей строки.

4. Находят новый псевдоплан и повторяют все действия, начиная с этапа 2.

Таблица 1

Пример 1.

Найти максимальное значение функции F=x₁+x₂+2x₃при условиях

Решение.

Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функцииF=x₁+x₂+2x₃при условиях

Умножим второе и третье уравнения системы ограничений последней задачи на –1 и перейдем к следующей задаче: найти максимум функции

F=x₁+x₂+2x₃ (4)

при условиях

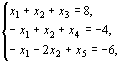(5)

x₁, x₂,…, x₅ ≥ 0 (6)

Составим для последней задачи двойственную задачу. Такой является задача, в результате решения которой требуется найти минимальное значение функции

F^*=8y₁ - 4y₂ - 6y₃, (7)

при условиях

(8)

y₂, y₃ ≥ 0 (9)

Выбрав в качестве базиса векторы P₃, P₄иx₁, составим симплексную таблицу (табл. 2) для исходной задачи (4) – (6).

Таблица 2

I	Базис	Сб	Р0	1	1	2	0	0
				P1	P2	P3	P4	P5
1	P3	2	8	1	1	1	0	0
2	P4	0	–4	–1	1	0	1	0
3	P5	0	–6	–1	–2	0	0	1
			16	1	1	0	0	0

Из этой таблицы видим, что планом двойственной задачи (4) – (6) является Y=(2;0;0).. При этом планеF^*=16. Так как в столбце вектораP₀таблица 2 имеются два отрицательных числа (–4 и –6), а в 4–й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс–метода переходим к новой симплекс–таблице. В данном случае это можно сделать, так как в строках векторовP₄ и P₅имеются отрицательные числа. Если бы они отсутствовали, то задача была бы неразрешима. Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектораP₀.В данном случае это число –6. Следовательно, из базиса исключаем векторP₅.Чтобы определить, какой вектор необходимо ввести в базис, находимmin (-Δ_j / a_3j), где a_3j < 0.Имеем

Значит, в базис вводим векторP₂.Переходим к новой симплекс–таблице (табл. 3).

Таблица 3

I	Базис	Сб	Р0	1	1	2	0	0
				P1	P2	P3	P4	P5
1	P3	2	5	1/2	0	1	0	1/2
2	P4	0	–7	–3/2	0	0	1	1/2
3	P2	1	3	1/2	1	0	0	-1/2
			13	1/2	0	0	0	1/2

Из этой таблицы видно, что получен новый план двойственной задачи Y=(2;0;1/2). При этом плане значение ее линейной формы равноF^*=13.Таким образом, с помощью алгоритма двойственного симплекс–метода произведен упорядоченный переход от одного плана двойственной задачи к другому.

Так как в столбце вектора P₀таблицы 3 стоит отрицательное число –7, то рассмотрим элементы 2–й строки. Среди этих чисел есть одно отрицательное –3/2. Если бы такое число отсутствовало, то исходная задача была бы неразрешима. В данном случае переходим к новой симплекс-таблице (табл. 4).

Таблица 4

I	Базис	Сб	Р0	1	1	2	0	0
				P1	P2	P3	P4	P5
1	P3	2	8/3	0	0	1	1/3	2/3
2	P1	1	1/3	1	0	0	-2/3	-1/3
3	P2	1	2/3	0	1	0	1/3	-1/3
			32/3	0	0	0	1/3	2/3

Как видно из таблицы 4, найдены оптимальные планы исходной и двойственной задач. Ими являются X^*=(14/3; 2/3; 8/3; 0) и Y^*=(2; 1/3; 2/3). При этих планах значения линейных форм исходной и двойственной задач равны между собой:F_max=F^*_min=32/3

Пример 2.

Найти максимальное значение функции F=2x₁+3x₂+5x₄при условиях

Решение.

Умножая первое и третье уравнения системы ограничений задачи на –1, в результате приходим к задаче нахождения максимального значения функции F=2x₁+3x₂+5x₄при условиях

Взяв в качестве базиса векторы P₃, P₄иP₅, составляем симплекс-таблицу (табл. 5).

Таблица 5

I	Базис	Сб	Р0	2	3	0	5	0
				P1	P2	P3	P4	P5
1	P3	0	-12	2	-1	1	0	0
2	P4	5	10	1	2	0	1	0
3	P5	0	-18	-1	2	0	0	1
			50	3	7	0	0	0

В 4-й строке таблице 5 нет отрицательных чисел. Следовательно, если бы в столбце вектора P₀не было отрицательных чисел, то в таблице 19 был бы записан оптимальный план. Поскольку в указанном столбце отрицательные числа имеются и такие же числа содержатся в соответствующих строках, переходим к новой симплекс–таблице (таблица 6). Для этого исключим из базиса векторP₅и введем в базис векторP₁.В результате получим псевдопланX=(6;0;-24;4)

Таблица 6

I	Базис	Сб	Р0	2	3	0	5	0
				P1	P2	P3	P4	P5
1	P3	0	-24	0	1/3	1	0	2/3
2	P4	5	4	0	8/3	0	1	1/3
3	P1	2	6	1	-2/3	0	0	-1/3
			32	0	9	0	0	1

Так как в строке вектора P₃нет отрицательных чисел, то исходная задача не имеет решения.