3.4. Симплексный метод решения задачи линейного программирования

Симплексный метод, известный в отечественной литературе под названием метода последовательного улучшения плана, впервые был разработан Данцигом в 1947г. Этот метод позволяет переходить от одного допустимого базисного решения к другому так, что значения целевой функции непрерывно возрастают. В результате оптимальное решение находят за конечное число шагов. Алгоритмы симплексного метода позволяют также установить, является ли задача ЛП разрешимой[5].

Алгоритм табличного симплексного метода

Запишем задачу ЛП в следующем виде:

Целевая функция: (1)

Система ограничений: (2)

где C=(c₁, c₂, …, c_n)- вектор коэффициентов целевой функции;

X=(x₁, x₂, …, x_n)^T – вектор-столбец решения(x_i0, i=);

A=(a_ij), i=, j= i=- матрица коэффициентов ограничений.

B=(b₁, b₂, …, b_m)^T– вектор-столбец правых частей системы ограничений.

Необходимо найти решение задачи ЛП:

вектор X=(x₁, x₂, …, x_n)^T, максимизирующий (минимизирующий) целевую функцию.

Шаг 1. Проверка неотрицательности правых частей системы ограничений

Если среди элементов вектор-столбца правых частей системы ограничений В имеетсяb_i<0, тогда умножаем коэффициентыi-ого ограничения на (-1) и меняем знак данного ограничения на противоположный.

Шаг 2. Переход от задачи минимизации к задаче максимизации

Меняем знаки при коэффициентах целевой функции на противоположные (3).

. (3)

Шаг 3. Переход к канонической форме

(4)

Вводим балансовую переменную x_n+1. Заносим эту переменную в вектор балансовых переменных, который представляет из себя разность между правой и левой частью ограничения:

Y=B-AX;

Y=(x_n+1, x_n+2, …, x_n+m)^T;

i-тое ограничение примет вид (5).

(5)

В целевую функцию балансная переменная вводится с нулевым коэффициентом, и целевая функция принимает вид (6).

(6)

Шаг 4. Нахождение первой крайней точки

Положим j=1. Взяв переменныеx₁, x₂, …, x_n за свободные и положив их равными нулю, аx_n+1, x_n+2, …, x_n+m– за базисные .находим первую крайнюю точку (7).

(7)

Шаг 5. Заполнение симплексной таблицы

Вводим A_k, составленный из коэффициентов переменнойx_k, и вектор С_Б– вектор составленный из координат, соответствующих базисным переменным.

Вычисляем симплексные разницы вj-той крайней точке по формуле (8).

, (8)

Заполняем симплексную таблицу (таблица 2) по указанным выше правилам.

Таблица 2

Базис	В	СБ	с1	c2	…	cn	cn+1	…	cn+m
			A1	A2	…	An	An+1	…	An+m
xn+1	b1		a11	a12	…	a1n	a1(n+1)	…	a1(n+m)
xn+2	b2		a21	a22	…	a2n	a2(n+1)	…	a2(n+m)
.	.		.	.	.	.	.	.	.
.	.		.	.	.	.	.	.	.
.	.		.	.	.	.	.	.	.
xn+m	bm		am1	am2	…	amn	am(n+1)	…	am(n+m)
		Z			…			…

Шаг 6. Анализ симплексных разностей

Если для j-той крайней точки все симплексные разности,k=, то эта точка оптимальная.Конец решения. Переходим к шагу 9.

Если есть столбец, в котором симплексная разность , а все элементы столбца,i=, то задача ЛП решения не имеет, т.к. целевая функцияне ограничена сверху.

В остальных случаях переход к шагу 7.

Шаг 7. Поиск направляющего элемента

Находим k₀– направляющий столбец. Выбираем столбец, в котором самая минимальная симплексная разность среди остальных симплексных разностей т.е.

,<0 (9)

Выбираем направляющую строку i₀ по условию:

,i=, >0 (10)

Если наблюдаем одинаковые , то получаем вырожденное решение (некоторые из ограничений задачи являются избыточными, т.е. оптимизируемая модель содержит неточности), оптимальное решение будет достигнуто в следующих итерациях. Выбираем строку с меньшим индексомi. Направляющий элемент , находится на пересечении направляющего столбца и строки.

Заполняем таблицу, соответствующую новому решению.

Шаг 8. Расчет элементов таблицы нового решения

Выполняем один шаг метода Гаусса, введя в базис вектор A_k0вместо вектораA_n0, имеющегоi₀ – координату, равную 1. Для этого используем следующие соотношения:

• новые элементы направляющей строки находятся:

,k=; (11)

• новые элементы направляющего столбца:

,i=, причемii₀;(12)

т.е. в направляющем столбце все элементы равны 0, а направляющий элемент равен 1.

• новые значения остальных элементов матрицы

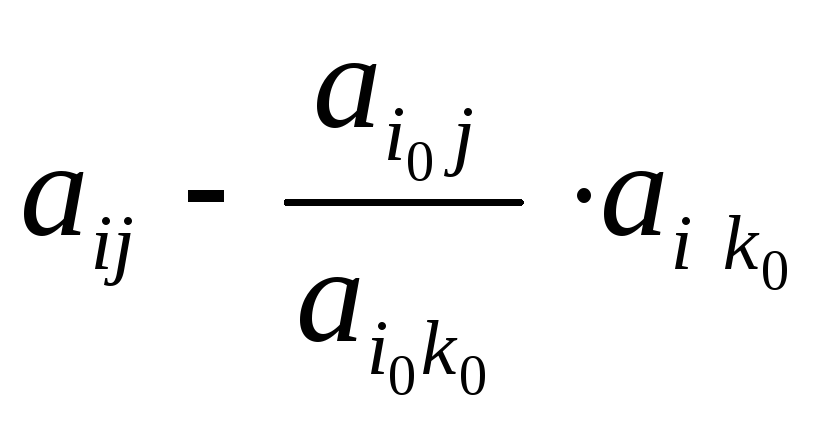,; (13)

• новые значения симплексных разностей

; (14)

Правильность вычислений контролируется по формулам непосредственного счета:

,k=(15)

Поучаем (i+j) крайнюю точку.

Если в данной точке все симплексные разности больше нуля () и существует такой небазисный столбец, что=0, то максимум достигается по крайней мере в 2 точках, т.е. имеет местоальтернативный оптимум. Переходим кшагу 9.

Если имеется хотя бы одна отрицательная симплексная разность для небазисного вектора, но его столбец содержит только не положительные элементы, то дальнейшая оптимизация невозможна. Целевая функция в этом случае не ограничена, и задача имеет пустое множество решений. Конец решения.

Пример 1

Минимизируйте функцию F=, при ограничениях

Пример 2

Минимизируйте функцию F=при ограничениях

Пример 3

Минимизируйте функцию F=при ограничениях

Пример 4

Найдите такие что выполняются ограничения

и функцияминимальна.