3. Принятие решений в условиях определенности. Линейное программирование

3.1 Постановка задач линейного программирования и исследование их структуры

Большинство задач, решаемых методами исследования операций, может быть сформулировано так[3]:

максимизировать

при ограничениях

где - целевая функция или эффективность системы (например, доход от производства каких-то изделий, стоимость перевозок и пр.);- варьируемые параметры;, …,- функции, которые задают ограничения на имеющиеся ресурсы.

Среди известных разделов математического программирования наиболее развитым и законченным является линейное программирование (ЛП). Несмотря на требование линейности целевой функции и ограничений, в рамки линейного программирования укладываются задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи, задачи теории расписаний и т.д.

Рассмотрим некоторые примеры задач линейного программирования.

Определение оптимального ассортимента. Имеютсярвидов ресурсов в количестваха₁, а₂, …, а_i, …, a_p и q видов изделий. Задана матрица, гдеa_ikхарактеризует нормы расходаi-го ресурса на единицуk-го изделия (k= 1, 2, …,q).

Эффективность выпуска единицы k-го изделия характеризуется показателемc_k, удовлетворяющим условию линейности.

Определить план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности принимает наибольшее значение.

Количество единиц k-го изделия, выпускаемых предприятием, обозначимx_k. Тогда математическая модель задачи имеет такой вид:

максимизировать (3.1.1)

при ограничении i=1, 2, …,p. (3.1.2)

Кроме ограничения по ресурсам (3.1.2), в модель могут быть введены дополнительные ограничения на планируемый выпуск продукции , условия комплектности для сборкидля всехi, j, k и т. д.

Оптимальное распределение взаимозаменяемых ресурсов. Имеютсяm видов взаимозаменяемых ресурсова₁, а₂, …, а_i, …, a_m, используемых при выполненииn различных работ в объемеb₁, b₂, …, b_n.

Заданы числа , указывающие, сколько единицj-й работы можно получить из единицыi-го ресурса, а такжеc_ij– затраты при изготовлении единицыj-го продукта изi-го ресурса.

Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность была наибольшей (или суммарные затраты - наименьшими).

Данная задача называется общей распределительной задачей.

Количество единиц i-го ресурса, которое выделено для выполнения работj-го вида, обозначимx_ij.

Математическая модель задачи такова:

минимизировать (3.1.3)

при ограничениях

j=1, 2, …,n; (3.1.4)

i=1, 2, …,m. (3.1.5)

Ограничение (3.1.4) означает, что план всех работ должен быть выполнен полностью, а ограничение (3.1.5) – что ресурсы должны быть израсходованы целиком.

В качестве примера такой задачи может служить известная задача о распределении самолетов по авиалиниям.

Задача о смесях. Имеется р компонентовi=1, 2, …,p, при сочетании которых в разных пропорциях получают различные смеси. В каждый компонент, а следовательно, и в смесь входитqвеществ. Количествоk-го веществаk=1, 2, …,q, входящее в состав единицыi-го компонента и в состав единицы смеси, обозначим соответственноa_ik иa_k. Полагают, чтоa_kзависит отa_ik линейно, т. е. если смесь состоит изx₁ единиц первого компонента иx₂ – единиц второго компонента и т. д., то

.

Задано р величин с_i, характеризующих цену, массу или калорийность единицыi-го компонента, иqвеличинb_k, указывающих минимально необходимое процентное содержаниеk-го вещества в смеси.

Необходимо определить состав смеси, при котором суммарная характеристика (цена, масса или калорийность) окажется наилучшей.

Обозначим через х₁, х₂, …, х_рвеличину компонента р-го вида, входящего в смесь.

Математическая модель имеет такой вид:

минимизировать (3.1.6)

при условии

k=1, 2, …,q. (3.1.7)

Условие (3.1.7) означает, что процентное содержание k-го вещества в единице смеси должно быть не меньше величиныb_k.

К этой же модели сводится, например задача определения оптимального рациона кормления скота.

Задача о раскрое материалов.На раскрой поступаетmразличных материалов. Требуется изготовить из нихkразных комплектующих изделий в количествах, пропорциональныхb₁, b₂, …, b_k(условие комплектности).

Пусть каждая единица j-го материала,l=1, 2, …,m, может быть раскроенаnразличными способами, так что при использованииi-го способа раскроя,i=1, 2, …,n, получитсяединицk-го изделия.

Определить план раскроя, обеспечивающий максимальное количество комплектов, если известно, что объем запаса j-го материала равен a_jединиц.

Количество единиц j-го материала, раскраиваемыхi-м способом, обозначимx_ij, а количество изготавливаемых комплектов изделий –х.

Математическая модель задачи такова:

максимизировать х

при условиях

(3.1.9)

(3.1.10)

Условие (3.1.9) означает ограничение запаса j-го материала, а условие (3.1.10) – условие комплектности.

Задачу линейного программирования можно сформулировать так:

максимизировать (3.1.11)

при условиях

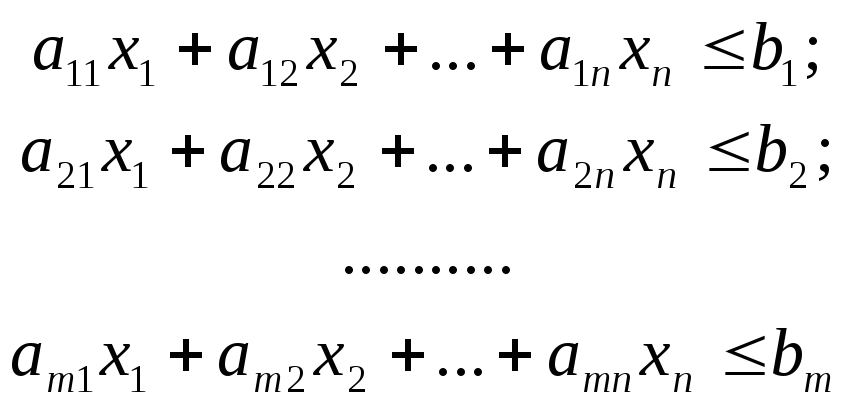(3.1.12)

и

(3.1.13)

Ограничения (3.1.13) называют условиями неотрицательности.

В данном случае все условия имеют вид неравенств. Иногда они могут быть смешанными, т. е. неравенства и равенства:

(3.1.14)

Если все ограничения задачи ЛП заданы в виде строгих равенств:

(3.1.15)

то данная форма называется канонической.

В матричной форме задачу ЛП записывают следующим образом:

максимизировать с^тх (3.1.16)

при условии

Ахb;

x0, (2.1.17)

где А – матрица ограничений размером (mn);b^(m1) – вектор-столбец свободных членов;х⁽ⁿ¹⁾ – вектор переменных;с^т = [c₁,c₂, …,c_n] – вектор-строка коэффициентов целевой функции.

Допустимым множеством решений задачи (3.1.11)-(3.1.13) называется множеством R(x) всех векторов х, удовлетворяющих условиям (3.1.12) и (3.1.13).

Очевидно, множество R(x) представляет собой выпуклое многогранное множество или выпуклый многогранник.

Решение х₀называется оптимальным, если для него выполняется условиес^тх₀ с^тх,для всеххR(x).

Отметим, что поскольку minf(x) эквивалентенmax[-f(x)], то задачу ЛП всегда можно свести к эквивалентной задаче максимизации.