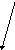Постановка задачи выбора в условиях неопределенности

Итак, для установления особенностей различных типов задач в условиях неопределенности рассмотрим несколько содержательных гипотетических примеров.

Пример 4.1

ЛПР - устроитель лотереи. Для привлечения участников игры им установлены п выигрышей (призов), равных по величине y₁, y₂, y₃,..., y_n. Величины y_i и вероятности P_i(a)=P(Y=y_i(a)) получения игроками этих выигрышей выбираются ЛПР и устанавливаются своей стратегией а так, чтобы риск финансового краха устроителя лотереи был бы в установленных границах, а прибыль от лотереи - не ниже требуемого уровня. Прямоугольная диаграмма распределения вероятностей величин выигрышей в лотерее представлена на рис. 4.1.

Рис. 4.1. Распределение вероятностей выигрыша в лотерее.

Пример 4.2

Имеются две лотереи. В первой можно выиграть 2000 руб. с вероятностью 0,9 и проиграть 800 руб. с вероятностью 0,1. Во второй лотерее с вероятностью 0,1 можно выиграть 10 000 руб. и с вероятностью 0,9 ничего не выиграть и не проиграть. Вычисления по формулам теории вероятностей показывают, что математические ожидания у той и другой лотереи одинаковы и равны 1000 руб., а дисперсии тоже одинаковы и составляют []. Означает ли такое совпадение числовых характеристик, что в этих лотереях будут играть примерно одинаковое число участников?

Пример 4.3

Продавец и покупатель ведут скрытый торг ("втемную") по купле-продаже некоего товара (например, акций на бирже). Суть торга - одновременное предъявление записок с указанием цены продажи и цены покупки соответственно. Стратегии покупателя - назначить цены a₁, а₂, а₃, a_m покупки так, чтобы купить подешевле, а стратегииb_1, b₂, b₃, b_n продавца - цены продаж, обеспечивающие наибольшую выгоду. При этом оба участника сделки понимают, что занижение цены покупки или чрезмерное завышение цены продажи могут привести к срыву сделки и поэтому они устанавливают цены в определенных пределах. После того как цены объявлены (записки вскрыты), поменять их нельзя, и, следовательно, сразу определится, состоится ли купля-продажа, окажется ли торг справедливым (цены равными), или же одна из сторон получит прибыль, а другая понесет убытки. Какие значения цен установить продавцу и покупателю?

Пример 4.4

Две крупные фирмы договариваются о разделе сфер влияния на рынке. Каждый предлагает свой план объемов сбыта каждой из сторон (естественно, более выгодный для себя); каждый может на переговорах реализовать только две стратегии: настаивать на собственных условиях или согласиться на предложения другой стороны. Если сложится ситуация, когда один (пусть - первый) участник переговоров добился принятия своего плана, а другой (второй) согласился с этим, то первый получает больше выгоды, чем второй. Зеркальная ситуация - это согласие первого участника на требования второго: в этом случае в более выгодном положении оказывается второй участник переговоров. Если участники будут жестко отстаивать каждый свой план, им не удастся договориться, и оба понесут существенные потери из-за конкуренции (аналогично будет и нелепая ситуация, когда каждый будет рьяно отстаивать предложения своего напарника). Как повести себя на переговорах: соглашаться или отказываться?

Пример 4.5

Составляется проект государственного бюджета на очередной год. Известно, что основную долю валютных поступлений в бюджет страна может получить за счет экспорта энергоносителей (нефть, газ). Цены на энергоносители в будущем году могут быть различными, в зависимости от ситуацийS_i на рынке, которые складываются под действием спроса и предложения, уровней добычи и примененных экономических санкций, тайных и явных соглашений между экспортерами или импортерами. О механизме этих факторов мало что известно, однако ясно, что заложенная в проекте бюджета цена на экспортируемые энергоносители (стратегияа ЛПР) будущая неизвестная сегодня конъюнктура рынка энергоносителей (ситуацияS_i) полностью определят степень исполнения бюджета по доходам и расходам.

В первом примере источником неопределенности выступает случайность стохастическая неопределенность. Здесь у ЛПР имеется полная информация и о возможных результатах, и о степенях возможности их появления (в виде вероятностного распределения на множестве результатов) для каждой стратегии. Оценка распределения вероятностей может быть либо "объективной" (то есть полученной по результатам статистических исследований именно этой сложившейся проблемной ситуации), либо "теоретической" (то есть полученной по формулам теории вероятностей путем расчета неизвестных вероятностей или вероятностных характеристик случайных событий, величин или процессов через известные, взятые из теории или из ранее накопленного практического опыта проведения аналогичных операций).

Второй пример - это иллюстрация известного факта, что одни люди при устранении проблем склонны принимать более рискованные решения, иногда нимало не заботясь о возможных печальных последствиях, а другие, наоборот всячески страхуются, стараются не рисковать, готовы получить более скромные результат, но наверняка, нежели гнаться за иллюзорными (в смысле маловероятными) гигантскими барышами. Другими словами, при анализе проблемных ситуаций в условиях стохастического риска необходимо учитывать индивидуальные особенности восприятия такого риска и отношение к нему для каждого по-своему.

Пример 4.3 - это простейшая иллюстрация антагонистической проблемной ситуации, в которой сталкиваются противоположные интересы нескольких (в данном примере двух) участников, причем одни из них выигрывают (получают дополнительный положительный эффект) только за счет того, что им проигрывают другие. Стратегия поведения в такой конфликтной ситуации зависит от взаимной информированности сторон, от умения рефлексировать (предсказывать) ответную реакцию оппонента, от способности подготовить и неожиданно для противника применить оригинальную стратегию и др. Напротив, пример 4.4 демонстрирует тот факт, что не всегда в конфликтных ситуациях интересы противников строго противоположны (не всегда строгий антагонизм), что каждый из них может преследовать собственные цели и измерять полезности ситуаций собственными критериями; этот пример также свидетельствует о том, что для анализа конфликтных ситуаций с нестрогим соперничеством следует преду­смотреть возможность получения информации (иногда частичной) о предполагаемых ответных реакциях и предпочтениях оппонента, возможность получения предложений о кооперировании и образовании коалиций.

Пример 4.5, в котором иллюстрируется ситуация с неопределенностью механизма операции (природная неопределенность), наводит нас на мысль о том, что обусловленный этой неопределенностью риск воспринимается ЛПР как некая степень неотвратимости неблагоприятного исхода или, наоборот, как абсолютная уверенность в безоблачном будущем: "Все будет хорошо!". Тут нужны особые формы учета подобного нестохастического риска.

Для обобщенного осмысления особенностей проблемных ситуаций, отмеченных нами в ходе анализа приведенных примеров, представим их модели графически.

Дерево основных типов условий и задач обоснования решений представлено на рис. 7.2. Схематические образы задач, представленные в прямоугольниках второго уровня иерархии на схеме, отражают главную суть различия - однозначность или многозначность исходов операции при одной и той же фиксированной стратегии а Алица, принимающего решения. Многозначность механизма неопределенности может быть генетически обусловлена разными факторами: случайностью, поведением других субъектов, участвующих (или оказавшихся втянутыми помимо их воли) в операции ЛПР, или просто отсутствие информации о степени возможности проявления тех или иных состояний в ситуации (например, отсутствие данных о конъюнктуре на том или ином рынке, об основных направлениях моды в будущем сезоне и т. п.).

Для простоты восприятия на рис. 4.2 представлены только образы задач с дискретным множеством исходов. Это обусловлено тем, что человек обычно склонен представлять любую "непрерывную" задачу в дискретном (атомарном) виде, выделяя лишь типичные исходы и ситуации, типичные или наиболее важные для него значения результатов и степени возможности проявления для них. К тому же такое "дискретное" представление задачи позволяет наиболее просто понять особенности тех или иных проблемных ситуаций и существо методов анализа решений в условиях неопределенности.

Так наивысшей степенью убедительности и достоверности суждений о возможных исходах операции, разумеется, обладают задачи обоснования решений в условиях определенности.

Генетические особенности механизма неопределенности условий ситуации
Случайность (стохастическая неопределенность)	Мотивы поведения (поведенческая неопределенность)	Отсутствие информации о природе явлений (природная неопределенность)
Р1 Р2 Р3 Рn у1(а) у2(а) у3(а) ... уп(а) ;	b1 b2 b3 bn у1(а, b1) у2(а, b2) у3(а, b3)... уп(а, bn)	s1 s2 s3 sn у1(а, s1) у2(а, s2) у3(а, s3) ... уп(а, sn)
Источники информации о возможности тех или иных исходов
Статистика	Разведка	Гипотезы
Типы задач обоснования решений
Задачи в условиях стохастического риска	Задачи в условиях нестохастического риска

Pиc. 4.2. Дерево основных типов условий и задач обоснования решений

Для остальных задач неопределенность исходов или неполнота (а иногда отсутствие) объективной информации о механизме ситуации порождают дополнительную психологическую напряженность, создают лишние трудности в решении проблем. Эти трудности обусловлены особенностями восприятия ЛПР возможностей подвергнуться потерям или убыткам в надежде получить более благоприятные результаты, особенностями восприятия величин предпочтительных значений результатов или величин возможных потерь и др.

Именно этим и отличаются задачи принятия решений в условиях риска (стохастического и нестохастического) от задач принятия решений в условиях неопределенности. Однако степень "рискованности" у подобных задач неодинакова. Наименьшим риском обладают ситуации принятия решений в условия стохастического риска, где информация о степени возможности исходов объективная (данные статистики). Наибольший риск присущ проблемным ситуациям обоснования решений в условиях природной неопределенности, где информация о степени возможности исходов вообще отсутствуют.

Это означает, что если для задач обоснования решений в условиях стохастической неопределенности еще можно предложить хоть какие-то объективные критерии (например, среднего или гарантированного результата), то для задач обоснования решений в условиях поведенческой и природной неопределенности приходится довольствоваться лишь субъективными оценками.

Вначале рассмотрим методы обоснования решений в условиях стохастической неопределенности, так как они являются основой для понимания подходов к обоснованию решений в условиях природной и поведенческой неопределенности.

Методы построения функции выбора в условиях стохастического риска

В случае стохастической неопределенности у ЛПР имеется полная информация о степени возможности тех или иных исходов операции для каждой стратегии в виде вероятностного распределения на множестве возможных результатов. Например, по итогам маркетингового исследования менеджер может получить полную статистику спроса на определенный вид товара в анализируемом сегменте рынка.

Часто необоснованно полагают, что использование каких-либо характеристик вероятного распределения интересующего ЛПР результата (чаще всего среднего значения результата и среднего квадратичного отклонения от этого значения) устраняет трудность выбора наилучшего решения. Однако, как пока­зывает практика, выбор на основе таких характеристик не всегда согласуется с личным представлениями ЛПР о лучшей альтернативе.

В частности, это объясняется также и тем, что, описывая задачи с риском, ЛПР редко использует такие теоретические понятия, как "распределение вероятностей", "случайная величина", "квантиль" и т. п. Вместо них человек обычно оперирует такими малоформализуемыми понятиями, как "шансы на выигрыш", "возможность неудачи", "тяжесть последствий" и др. Он их воспринимает как более привычные, а потому и более надежные. Пусть, ЛПР предлагают стать инвестором некоторого коммерческого проекта и вложить в него 1000 долл. В бизнес-плане фигурируют следующие оценки: предполагаемая инвестиция с вероятностью 0,3 может принести прибыль в 1000 долл., с вероятностью 0,1 прибыль не окажется ниже 500 долл., с вероятностью 0,5 инвестицию удастся не потерять, а с вероятностью 0,1 инвестора постигнет крах (потеря вложенных в проект денег). Обычно, анализируя подобные оценки исходов, ЛПР прежде всего обращает внимание на "успех" предприятия (равный величине менее 500 долл. и не более 1000 долл.) и оценивает его вероятность (не менее 0,4), а затем анализирует "неудачу" (потерю инвестиции) и неблагоприятного исхода (в нашем примере 0,1). Как оценить выгодность инвестиционного проекта? Стоит ли на него решаться?

При анализе подобных "стохастических" решений мы можем рекомендовать только одно - вновь каким-то образом опереться на принцип убедительности надежности рекомендаций для выбора. Именно поэтому на начальном этапе формирования функции выбора ЛПР следует руководствоваться уже методическим подходом - принципом Родена. Напомним, что принцип Родена указывает на то, что наилучшее решение следует искать называемых недоминируемых альтернатив.

Таким образом, остается только переформулировать этот принцип применительно к стохастическому риску.

Хорошо согласуется с данными практики следующая формулировка принципа стохастического доминирования:

«Тот вариант решения лучше, для которого при любых фиксированных уровнях значений требуемого результата вероятность получения возможных результатов, по величине таких же или превосходящих требуемый окажется выше».

Другими словами, для того чтобы установить какой из двух вариантов решения, а илиb, имеющихся в распоряжении ЛПР, лучше, ему нужно последовательно "перебрать" все возможные значенииt требуемого результата и проверить, какая из вероятностей,P(Y(b)t) илиP(Y(а)t), получения возможных результатов окажется больше. При этом черезY обозначено случайное значение возможного результата у,ab, а предпочтительнееb.

Если для всех у, например, окажется, чтоР(У(а) у) P(Y(b)у) то, следовательно,аb и альтернативаb стохастически доминируется. Формальный вид этого правила доминирования (стохастическое доминирование типа 1 представляется выражением

, (4.1)

где =P(Y(a) < у) - функция распределения результатаYдля альтернативыa.

Очевидно, что отношение стохастического доминирования первого задаваемое выражением (4.3), несвязно, так как неравенство в правой части выражения (значений функции распределения случайного результата) может не выполняться для всех значений результата. Это положение демонстрируют графики для трех вариантов проведения операции, показанные на рис. 4.3. С помощью этих графиков легко установить, что альтернатива b стохастически доминируется альтернативой а, альтернативы а и с несравнимы по сформулированному принципу стохастическою доминирования первого типа. Именно варианты а и с следует оставить для дальнейшего анализа их предпочтительности.

Рис. 4.3. Графики функций распределения: а - ситуация 1; б - ситуация 2

Остановимся более подробно на различиях в несравнимости оставленных ва­риантов.

Анализ рис. 4.3, а показывает, что несравнимостьа ис вызывается только тем, что для распределения, соответствующего альтернативеа, несколько выше вероятность получения результатов хуже весьма малого значенияy₁, чему распределения, соответствующего вариантус. Поэтому на практике может оказаться, что в ситуации, сходной с той, которая отражена на рис.4.3,а, целесообразнее рискнуть (тем более что риск незначительный) и отдать предпочтение вариантуа по сравнению с вариантом с.

Это обстоятельство может быть учтено, если используется следующее отно­шение квазипорядка (стохастическое доминирование типа 2):

, . (4.2)

Оказывается, что согласно правилу (7.2) стратегия а, приводящая к распреде­лениюпредпочтительнее некоторой стратегииd, достоверно приводящей к неслучайному результатуy(d) = M[Y(a)], совпадающему со средним значением результата для стратегииа.

Другими словами, если ЛПР всегда, при любых условиях настаивает на том, чтобы обязательно реально проводить планируемую операцию, и не согласно с тем, чтобы ему назначили достоверную компенсацию в виде среднего результата операции за то, что он откажется от ее проведения, то такое ЛПР следует характеризовать как лицо, склонное к рискованным операциям ("склонный к риску").

Ситуация, представленная графически на рис. 4.3, б, в этом смысле противоположна только что рассмотренной, и здесь чаще всего вряд ли следует рисковать ради получения результатов уy₂ и отдавать предпочтение вариантуапо сравнению с вариантомс, так как вероятность рассматриваемого события весьма мала для каждой из стратегий. Это обстоятельство может быть учтено, если используется следующее отношение квазипорядка (стохастическое доминирование типа 3):

, . (4.3)

Можно утверждать, что ЛПР всегда предпочитающее получение среднего результата операции наверняка, лишь бы эту операцию реально не проводить и самому в ней не участвовать, должно квалифицироваться в отношении статистического риска как "несклонное к риску".

Функции выбора, построенные на основе принципов стохастического доминирования, ввиду их слабой разрешающей способности незначительно сокращают объем исходного множества альтернатив. Всякое дальнейшее суждение множества выбора возможно лишь при использовании дополнительной информации о предпочтительности того или иного сочетания компонентов риска (величин выигрышей и потерь и вероятностных распределений на их значениях).

Эта информация используется в эвристических и аксиоматических правилах (принципах) выбора: предпочтительность в среднем, предпочтительность по кучности результатов, предпочтительность по уровню гарантии получения результатов или предпочтительность по уровню самого гарантированного результата и др.

Рассмотрим способы построения функции выбора на основе этих принцип, считая, что на результатах у(а) уже построен критерийW(a), измеряющий предпочтительность полученных результатов.

Принцип среднего результата. Этот принцип состоит в том, что для фиксированной стратегииа случайная величинаW(a) заменяется ее средним значением .Оптимальная стратегия определяется так:

а*: max ,.

Распространенность этого показателя объясняется тем, что он не требует задания каких-либо вспомогательных величин (типа уровня результата или степень гарантии).

Принцип кучности результатов. Каждая стратегияа оценивается какой-нибудь характеристикой разброса случайной величиныW(a). Та стратегия предпочтительнее, у которой рассеивание возможных исходов меньше. Практически принцип кучности результатов применяется в тех случаях принятия решения в условиях риска, когда среднее значение для всех стратегий одинаково (например, равно нулю).

В роли минимизируемой функции чаще всего используется дисперсия D(a) или среднее квадратическое отклонение (СКО):

а*:min D(a),

или

а*:min ,причем и.

Принцип вероятностно-гарантированного результата. Для выбранной

стратегии а распределение случайной величины показателя эффективностиW(a) известно. Если задать требуемый уровень результатаb, то можно определить вероятность того, чтоW(a) примет значение не меньшеb:

P(W(a)b)=1-F(b).

При этом оптимальной считается та стратегия, которой соответствует наибольшая вероятность получения результата не хуже b:

.

Наоборот, если задать степень гарантии - вероятность то можно определить соответствующий результат - числоb:

b(a) = F-1(1-Р^треб).

При заданной степени гарантии Р^требта из стратегий предпочтительнее, которой соответствует наибольшая величина результата, полученного с вероятностью, не меньшей чемР^треб.

.

Результаты, полученные путем применения принципа вероятностно-гарантированного результата, обладают неустойчивостью в том смысле, что малые изменения величин Р^треб илиb нередко приводят к кардинальному изменению предпочтения. Эта ситуация приведена на рис. 4.4.

Рис. 4.4. Неустойчивые ситуации

Показатели эффективности определяют по формулам:

При назначении в качестве требуемого результата стратегияv> а, так Им кW_v>W_a, а при требуемом результате, наоборота > v.

Рассматриваемый принцип допускает, чтобы шкала показателя W(a), была всего лишь порядковой.

Все рассмотренные принципы принятия решений в условиях стохастического риска сводят исходную задачу с показателем W(a), являющимся случайной функцией стратегииа, к задаче оптимизации с одной числовой функцией.

Заметим, что, хотя функции выбора, использующие показатель вероятностной гарантии, более информативны по сравнению со случаем использования и качестве показателя отдельных моментов распределения, в вычислительном и отношении показатель вероятностной гарантии сложнее. Кроме того, получаемые с его помощью решения, как правило, критичны к выбору требуемого уровня у^тр результата.

Показатели среднего результата проще, так как не требуют информации о величинах у^тр, поэтому они получили весьма широкое распространение в практике. Однако использование показателя среднего результата оправдано лишь в том случае, когда операция носит массовый характер и(или) обладает свойством повторяемости. Если операция "уникальна", то предпочтение следует отдать показателям вероятностной гарантии либо, если это по каким-либо причинам невозможно, использовать в дополнение к показателю среднего результата показатели его кучности.

ЛПР редко ограничивается использованием только объективных характеристик распределения результата. Практика показывает, что величина риска является одним из главных факторов при анализе альтернатив. Так, во многих случаях ЛПР принимает во внимание два фактора: среднюю величину выигрыша и кучность результатов. Исследования показывают, что для каждой величины дисперсии результатов существует вполне определенная компенсирующая величина среднего результата, делающая вариант решения вполне привлекательным. Другими словами, человек может пойти на риск не потому, что риск для него "привлекателен" (имеет положительную ценность), а потому, что он рассчитывает на получение более высокого положительного эффекта.

Учитывая перечисленные обстоятельства, часто при обосновании решений в условиях стохастического риска используют следующий критерий, значение которого максимизируют:

где 0 <<1 - коэффициент, учитывающий отношение ЛПР к риску.

Если ЛПР абсолютно равнодушно к риску, то полагают= 1, если абсолютно предрасположено, то= 0. Если ЛПР равнодушно к риску, то величинувыбирают из интервала [], при этом полагают;

Если выбрать коэффициент из интервала [v,l), то это значит, что ЛПР не­склонно к риску, а если из интервала (0,], то оно склонно к риску в той или иной степени.

Более точный учет особенностей отношения ЛПР к стохастическому риску возможен только на основе аксиоматических подходов к построению функции выбора. Один из таких подходов основан на использовании в качестве функции выбора так называемой функции полезности.

Обозначим функцию полезности результата у черези(у). Согласно аксиома­тической теории полезности отношение предпочтения на множестве альтернатива моделируется с использованием математического ожиданияМ[и(у(а))] функции полезности для этих альтернатив:

, (4.4)

Важным свойством функции полезности является то, что допустимым преобразованием для нее является линейное с положительным коэффициентом пропорциональности. Это значит, что если и(у(а)) - функция полезности, моделирующая предпочтения ЛПР в ситуациях со стохастическим риском, то множествоU(y(a)) функций, полученных из исходной по формуле

U(y(a))={ku(y(a)) + c, k>0},

будут точно так же моделировать предпочтения ЛПР и точно так же отражать его отношение к риску, как и исходная.

Это означает, что при построении функции полезности можно произвольно выбирать начало отсчета с и единицу измеренияk (то есть функция полезности задается в интервальной шкале). Рассмотрим предпосылки, используемые при построении функции полезности. Для этого вначале введем понятие лотереи как модели выбора в условиях стохастической неопределенности.

Лотереейlot называется пара(Y, Р), гдеY = {y₁, у₂, у_n] множество возможных значений результата у,Р = (p₁,р₂, р_т) вероятностное распределение на результатах.

В общем случае можно рассматривать лотереи с непрерывными значениями результата, а также лотереи с векторными результатами и составные лотереи (где результатом одной лотереи является другая лотерея). Примеры простой и составной лотерей приведены на рис. 4.5.

Заметим, что неслучайный результат можно формально представить вырожденной лотереей (где этот результат получается с вероятностью, равной единице).

а б

Рис. 4.5. Лотереи: а - простая; б - составная

Оказалось, что психологические особенности человека таковы, что ему очень трудно сравнивать лотереи с большим числом выигрышей. Любому человек гораздо проще иметь дело с такими лотереями, в которых только по два исхода. В подобных ситуациях ЛПР обычно сравнительно легко отвечает на вопросы типа: "За сколько вы согласны отступиться от участия в лотерее?" или "В сколько вы оцениваете лотерею, если вам предложат ее продать?" Особенно просто это выходит, если в лотерее эти два результата имеют смысл «наилучшего» (обозначим его через у⁺) и «наихудшего» (соответственно) из возможных.

Так, для лотереи (Y, Р), в которой результатy₁=у⁺ получается с вероятностьюр₁=р, а результату₂ = - с вероятностьюр₂= 1 - р, ЛПР может достаточно уверенно указать такое значение результата у, находящегося по предпочтительности между наилучшим у⁺и наихудшимрезультатами), что для ЛИ будет безразлично, участвовать ли в лотерее(Y, Р) или получить результату наверняка.

Так как функция полезности верна с точностью до положительного линейного преобразования, то для установления начала отсчета и единицы измерения удобно задать оценки для любых двух результатов, а затем остальные соизмерить с ними. В качестве таких результатов как раз и выбирают наиболее предпочтительный у⁺и наименее предпочтительный и полагаюти(у⁺) = 1, аи() = 0.

При соизмерении произвольного результата ус наилучшим и наихудшим результатами используется следующее допущение, которое называется правилом замены.

Правило замены. Если в исходной лотерее lot = (Y, Р) любой из результатов у заменить на эквивалентный ему по предпочтительности, то для ЛПР будет безразлично, в какой из лотерей, исходной или новой, участвовать. Результат у в этом случае заменяют на лотерею вида у⁺ с вероятностью р(у) и с вероятностью 1-р(у). Такая лотерея называетсябазовой.

Вероятность р(у) в базовой лотерее должна выбираться такой, чтобы базовая лотерея была эквивалентна по предпочтительности вырожденной лотерее, приводящей достоверно к результатуу. Схема эквивалентной замены базовой лотереи на вырожденную представлена на рис. 4.6. Поскольку полезность наилучшего результата равна единице (а наихудшего - нулю), то получается, чтои(у) =р(у).

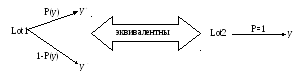
Рис. 4.6. Схема эквивалентной замены базовой лотереи на вырожденную

Описанный способ построения и(у) можно достаточно успешно применять для установления предпочтений на множестве стратегий при числе исходов в лотереях не более 10...20. В задачах со значительным числом исходов (более 30) установление отношения предпочтения на лотереях удобнее производить другим способом, основанным на оценивании значений функции полезности в отдельных точках и ее последующей аппроксимации. Этот подход является более универ­сальным, так как позволяет рассматривать не только дискретные вероятностные распределения результатов, но непрерывные и смешанные распределения.

Согласно этому способу вначале устанавливают тип отношения ЛПР к риску (несклонный, склонный, безразличный) для различных интервалов возможных значений результатов. В общем случае на этом этапе может быть выявлена и психологическая доминанта ЛПР. Тип отношения ЛПР к риску на том или ином интервале возможных значений характеристики вводится на основе досто­верного (детерминированного) эквивалента лотереи.

Достоверным эквивалентом лотереи lot = (Y,Р) называется величинаy_d, такая, что ЛПР безразлично, получить ли результатy_d наверняка или участво­вать в лотерееlot.

Оказывается, что по величине детерминированного эквивалента можно судить о типе отношения ЛПР к стохастическому риску. Так, если детерминированный эквивалент y_d лотереи меньше математического ожиданияM_y результатов лотереи, то ЛПР несклонно к риску, еслиy_d > M_y - склонно к риску, а если они равны - ЛПР равнодушно к риску.

Заметим, что если ЛПР несклонно к риску, то его функция полезности строго вогнута. Действительно, так как для ЛПР, несклонного к риску, предпочтительнее получение среднего выигрыша наверняка, нежели участие в лотереи со случайными исходами, то и(М_y) > М[u(y)], что для базовой лотереи приводит к неравенству вида

0<p<1,

что соответствует математическому определению строгой вогнутой функции.

Аналогично можно показать, что функция полезности на интервале [,y⁺] по пяти точкам с использованием равновероятной бинарной лотереи, показанной на рис. 4.7.

Рис. 4.7. Равновероятная бинарная лотерея

Будем обозначать ее через lot 0,5(y₁, у₂). Отличительной особенностью этой лотереи является то, что появление каждого из результатовy₁, у₂ возможно с одинаковой вероятностью.

Алгоритм построения функции полезности по пяти точкам включает выполнение следующих шагов:

1. положить и() = 0,и(у⁺) = 1;

2. определить достоверный эквивалент y_d = y_0,5 лотереиlot0,5(, у⁺) и положитьu(y_0,5) = 0,5;

3. аналогично определить достоверные эквиваленты у_0,25и у₀,₇₅ лотерейlot0,5(, у_0,5) иlot0,5(у_0,5, у⁺) соответственно и положитьи(у_0,25) = 0,25,и(у₀,₇₅) = 0,75;

4. проверить согласованность полученных результатов, определив достоверный эквивалент lot0,5 (у_0,25, у₀,₇₅) и сравнить с результатомy_d = у₀,₅полученным на шаге 2; если отличие незначительно, то перейти к следующему шагу; в противном случае указать ЛПР на противоречие в его ответах и повторить шаги 2...4 вновь;

5. нанести полученные точки на график и провести плавную кривую, соответствующую ранее выявленному типу отношения ЛПР к риску и хорошо согласующуюся с указанными точками; при необходимости аппроксимировать полученную кривую одной из аналитических зависимостей.

Анализ решений в условиях поведенческой неопределенности

Теория, занимающаяся анализом проблемных ситуаций, в которых ведущим типом неопределенности является нестохастическая (поведенческая или природная), и разработкой рекомендаций по рациональному поведению в них, носит интегрированное название теория игр. Сам термин "игра" в этом случае обозначает специальную модель особой проблемной ситуации, в которой либо сталкиваются интересы нескольких субъектов, вовлеченных в операцию, либо неясна природа явлений, обусловливающих действие механизма ситуации.

Основной принцип обоснования решений в игре - принцип наибольшего гарантированного результата. Понятие гарантированного результата базируется на гипотезе о крайне неблагоприятном стечении обстоятельств для ЛПР. Согласно принципу наибольшего гарантированного результата рациональным следует считать такое поведение, которое обеспечивает наилучший результат из самых неблагоприятных. В силу этого данный принцип часто называют принципом максимина (хотя, как это будет показанное ниже, подобное утверждение не всегда семантически корректно).

Рассмотрим вначале методы построения функции выбора в условиях поведенческой неопределенности.

При анализе ситуаций в условиях поведенческой неопределенности помимо принципа наибольшего гарантированного результата руководствуются также принципом равновесия. Принцип равновесия означает, что рациональным поведением субъектов операции следует считать такое, при котором каждый из них стремится к ситуации, обеспечивающей каждому наибольший выигрыш и отклонение от которой не выгодно никому.

Количественный анализ возможных альтернатив в условиях поведенческой неопределенности предполагает решение следующих основных задач:

• формирования множеств возможных стратегий субъектов операции ("игро­ков");

• количественной оценки величин результатов, получаемых субъектами в каждой из ситуаций;

• выделения множества недоминируемых стратегий для каждого из субъектов операции;

• выбора наилучшего варианта решения на основе принципов рационального поведения.

Таким образом, модельными компонентами игр являются игроки, модели целей игроков, доступная игрокам информация для принятия решений и правила осуществления "ходов" в игре.

В зависимости от того, как конкретно выражаются перечисленные элементы игр, их относят к тому или иному классу, а для каждого класса разрабатывал специальные, наиболее удобные способы отыскания наилучших стратегий им игроков. В качестве классификационных признаков, характеризующих ту или иную игру, обычно используют:

• количество субъектов (игроков), интересы которых затрагиваются при проведении операции ЛПР и которые могут влиять на ее результаты, а также возможность создания коалиций;

• тип отношений между игроками, возникающих при стремлении игроков обеспечить наивыгоднейшее положение в игре для себя;

• возможность обмена информацией между игроками в целях сообщения своих возможных стратегий и оценочных функций;

• типы множеств стратегий игроков (дискретные, непрерывные).

По количеству субъектов, интересы которых пересекаются в операции, выделяют парные и множественные игры (игры n-лиц), а по возможности создавать коалиции - бескоалиционные и коалиционные.

Тип отношения между игроками определяется тем, как соотносятся цели игроков (ЛПР и других субъектов операции). Если цели игроков совпадают с целями ЛПР, то это отношение можно охарактеризовать как содействие. Такая ситуация может быть сведена к задаче обоснования решений либо в условиях неопределенности (ЛПР точно знает, как поведут себя содействующие субъекты) либо в условиях неопределенности (действуют только случайные или природно-неопределенные факторы).

Если интересы других субъектов операции не совпадают с интересами ЛПР и тем более если они им противоположны, то тип отношения между игроками может квалифицироваться в широких пределах - от соперничества до прямого противодействия. В этом случае проблемная ситуация приобретает конфликтную окраску, и поэтому называется конфликтной ситуацией. Таким образом, типу соперничества выделяют антагонистические и неантагонистические классы игр.

В зависимости от того, предоставляется или не предоставляется игрокам возможность обмена информацией в целях сообщения своих возможных стратегий и оценочных функций, различают кооперативные и некооперативные игры.

Если множества стратегий игроков дискретные, то игры называются матричными (или конечными), в противном случае - бесконечными.

Изучение методов построения функции выбора в условиях поведенческой неопределенности целесообразно начать с анализа парных бескоалиционных некооперативных антагонистических матричных игр.

Для проведения формального анализа обозначим через v₁(a,b), v₂(a,b)оценочные функции (функции выигрыша) 1-го и 2-го игроков соответственно заданные на множестве(а,b) ситуаций игры и сворачивающие значения векторных результатов в скалярные.

Наиболее полной информацией, позволяющей получить решение антагонистической игры, являются сведения о том, что функции v₁(a,b), v₂(a,b),определенные на множестве ситуаций игры, удовлетворяют соотношениюv₁(a,b)=-v₂(a,b), то есть 1-й игрок выигрывает ровно столько, сколько ему проигрывает 2-й и наоборот. Поэтому при анализе подобных игр можно использовать одну функцию выигрыша, обычно 1-го игрока, полагаяv(a,b) = v₁(a,b).

Игра со строгим соперничеством, удовлетворяющая записанному соотношению, называется антагонистической.

При анализе антагонистических игр вначале определяют гарантированный результат применения ЛПР каждой из его стратегийa, то есть для каждой стратегии 1-го игрока устанавливают величину

.

Затем определяют стратегию a*, обеспечивающую наибольший гарантированный результат 1-му игроку:

и саму величину наибольшего гарантированного результата 1-го игрока. Стратегияа* и величинанаибольшего гарантированного выигрыша называются максиминными.

Учитывая целевое устремление 2-го игрока (максимизация v₂(a,b)), определяют гарантированный результатv⁺(a):

и стратегию *, обеспечивающую "наибольший" гарантированный результат для 2-го игрока:

а также саму величину v⁺=v⁺(*) наибольшего гарантированного результата 2-го игрока. Стратегия* и величинаv⁺наибольшего гарантированного выигрыша называются минимаксными.

Величины иv⁺ называются такженижней иверхней ценами игры соот­ветственно. Соотношение между ними устанавливает основная теорема теории игр, а именноv⁺. Таким образом, при рациональном поведении 1-й игрок не может выиграть меньше чем, а 2-й не может проиграть ему больше чемv⁺.

Стратегии игроков, определяемые по правилам максимина и минимакса, будут удовлетворять принципу равновесия, если реализуемая при этом ситуация (а*b*) обеспечивает равенство нижней и верхней ценыигры, то естьv(а*,b*) ==v⁺. В этом случае говорят, что играимеет ситуацию равновесия в чистых стратегиях.

Поскольку ситуация в максиминных стратегиях не всегда является равновесной, будем равновесные стратегии и соответствующие им равновесные ситуации обозначать (а₀,b₀). Для равновесных ситуации справедливо следующее отношение (седловая точка):

v(a,b₀) v(a₀,b₀) v(a₀,b),

которое формально представляет условие равновесия по Нэшу для антагонистических игр.

От равновесной ситуации не выгодно отклоняться ни одному из игроков, так как она сформирована из стратегий, доставляющих наибольший гарантированный результат каждому из игроков. Именно равновесная ситуация может рассматриваться в качестве решения игры.

Заметим, что необходимым условием существования равновесной ситуации, (седловой точки) является непрерывность функции v(a,b) на выпуклом множествеА Вситуаций игры. Достаточным условием существования равновесной ситуации является вогнутость функцииv(a,b) поаи выпуклость поb.

Равновесных ситуаций может быть несколько. При этом все равновесные ситуации для случая антагонистических игр дают одинаковое значение игры. Кроме того, если (a',b') и (a'',b'')- две равновесные ситуации, то равновесными оказываются также и ситуации (a',b'') и (a'',b'), причем все они дают одинаковое значение игры. В то же время последнее утверждение не обладает достаточностью, то есть если в какой-то ситуации значение функции выигрыша совпадает с ценой игры, то это не означает, что данная ситуация равновесная.

Матричные игры

Матричная игра является частным случаем антагонистической игры, когда множества стратегий игроков конечны. Это значительно упрощает анализ игры и позволяет разработать эффективные методы отыскания равновесных решений. Каждую стратегию из дискретных множествА илиВ называют чистой стратегией. Для удобства анализа перейдем от прямого поименования(а, b) ситуаций, к их условному обозначению(i,j) через номера стратегий игроков, причемi-номер стратегии 1-го игрока, аj- 2-го игрока. Количества стратегий 1-го и 2 игроков будем полагать равнымит и п соответственно[1].

Поиск решения игры в чистых стратегиях осуществляют следующим образом:

• отыскивают максиминные стратегии i*, j*;

• вычисляют величины выигрышей иv⁺и сравнивают их по величине (если они равны, то существует равновесная ситуация (i₀, j₀) в чистых стратегияхi*, j* иначе ситуации равновесия в чистых стратегиях не существует.

В целом матричная игра - это отличная модель дикой конкуренции на рынке. Чаще всего, как и в реальной жизни, матричная игра не имеет ситуации равновесия в чистых стратегиях. Подобная коллизия заставляет игроков адаптироваться друг к другу, выдвигать последовательно усложняющиеся гипотезы об ответных реакциях противника и собственных контрмерах. Такое поведение называют рефлексивным. Оно побуждает игрока отклоняться от своей максиминной (минимаксной) стратегии с целью улучшения значения выигрыша в свою пользу. Однако чтобы реализовать адаптивный подход, игрок должен использовать текущую информацию, следовательно, игра должна состоять из нескольких «партий» (чем больше, тем лучше). В этом случае использование принципа адаптивности сведется в конечном итоге к выбору рационального сочетания (частоты применения) чистых стратегий.

Формальной причиной, порождающей отсутствие ситуации равновесия в чистых стратегиях, является невыполнение необходимого и достаточного условий существования седловой точки. Чтобы удовлетворить этим условиям, прибегают к смешанному расширению игры, вводя в дополнение к чистым так называемые смешанные стратегии. По сути это реализация в каждой "партии" игры какой-то одной из чистых стратегий, которую "выбирает" случай в соответствии с определенными вероятностями. При такой организации собственного поведения, при такой стратегии ЛПР противник уже не может уверенно рефлексировать и эффективно подстраиваться к возможным ходам ЛПР, не мо­жет с уверенностью предсказать более вероятный ход его мыслей. Трудно другому предсказать то, о чем первый даже и сам не знает!

Смешанной стратегией 1-го игрока на множестве чистых стратегий 1, 2, …, т называется вероятностное распределениеР = (p₁, р₂ ,р_m) на них, а смешанной стратегией 2-го на множестве чистых стратегий 1, 2, …,п - вероятностное распределениеQ = (q₁, q₂, q_n).

Смешанное расширение игры приводит к тому, что в качестве выигрыша игроков необходимо рассматривать математическое ожидание

(4.6)

где - выигрыш 1-го игрока в ситуации(i,j).

Функция Mpq теперь является непрерывной на выпуклом множествеPQ по каждому из аргументовР и Q.

Общим подходом к решению игры в смешанных стратегиях является сведе­ние ее к задаче линейного программирования.

Для этого вначале игру редуцируют (исключают доминируемые стратегии игроков). Затем матрицу игры подвергают линейному преобразованию (это всегда можно сделать, так как функция ценности задается в интервальной шкале) с целью обеспечить неотрицательность величин выигрышей:

,,i=1,m, j=1,n; h0,

где - элементы преобразованной платежной матрицы игры.

Согласно выражению (7.6) математическое ожидание выигрыша будет в этом случае положительным: Mpq > 0. Исходя из определения максиминной стратегии, применение1-м игроком смешанной стратегииР* должно для любой стратегии 2-го игрока давать результат не ниже некоторой величиныМ* (наибольшего гарантированного результата1-го игрока), то есть

Разделим обе части выписанной системы неравенств на величину М* > 0. В результате получим систему неравенств для любой стратегии j

(4.7)

Так как величины p_i0 связаны соотношением

то, разделив обе части его на величину М*, получим

(4.8)

Введем новую переменную

Переписывая систему неравенств (7.7) и равенство (7.8) с использованием новой переменной и учитывая стремление 1-го игрока максимизировать величину, приходим к следующей задаче линейного программирования:

(4.9)

при ограничениях:

Аналогично формируется задача линейного программирования для определения оптимальной смешанной стратегии второго игрока:

(4.10)

при ограничениях:

После получения решения m* иn* задач (7.9) и (7.10) оптимальные смешанные стратегии Р* иQ* игроков определяют обратным пересчетом.

В частных случаях (когда у одного из игроков только две стратегии) решение игры может быть найдено графическим способом. Поясним его на примере решения игры 2. Очевидно, еслиp₁=p - вероятность применения первой стратегии, тор₂=1-р и можно использовать только одну переменную (например,p₁) для описания среднего результата игры.

Рассмотрим игру 2, матрица которой имеет

Смешанную стратегию 1-го игрока представим вектором

Р = (p, 1-p),0р1.

Условия игры записываются так:

М* = max [min М(р, j)]

,

где

Семейство графиков для различныхпоказано на рис. 4.8. Точке р* соответствует максимальная ордината нижней огибающей семейства прямых.

Число р*, характеризующее максиминную стратегию для 1-го игрока, в данном случае определяется путем решения уравнения:

Затем определяется значение выигрыша:

Если требуется решить игру т2,то графически это проводится аналогично.

Даже если реальные отношения между субъектами операции носят откровенно конфликтный характер, как на "диком" рынке, где сталкиваются противоположные интересы сторон, то моделирование подобной проблемной ситуации антагонистической игрой может рассматриваться лишь как первое приближение в анализе конфликта. Это обусловлено тем, что фактически никогда ЛПР не допускает полного неприятия риска, а также тем, что интересы сторон не являются строго противоположными. Как правило, последнее – это следствие того, что стороны используют разные оценки полезности ситуаций.

Рис. 4.8. Семейство графиков игры 2М

Поэтому более адекватной моделью проблемной ситуации является модель, в которой фигурируют две различные функции выигрыша v₁(a,b) иv₂(a,b). Модели такого типа называютсяиграми с нестрогим соперничеством (неантагонистические игры). Для парных бескоалиционных неантагонистических игр ситуация равновесия по Нэшу имеет вид:

(4.11)

где v₁иv₂- функции выигрышей 1-го и 2-го игроков соответственно.

Система (4.11) по форме несколько отличается от неравенства (4.5) для седловой точки в антагонистической игре. В то же время это различие носит более глубокий характер. В антагонистической игре отклонение одного из игроков oт ситуации равновесия приводит к уменьшению его выигрыша, а следовательно, к увеличению выигрыша второго. В неантагонистической игре такое же отклонение может по-разному повлиять на выигрыш 2-го игрока. Если оба игрока отклонятся от равновесной ситуации, то в результате они могут оказаться в ситуации (а,b), в которой выигрыш каждого из них может остаться прежним, может увеличиться или уменьшиться.

Кроме того, если в антагонистических играх несколько равновесных ситуаций в чистых стратегиях, то попарные пересечения их стратегий также образуют равновесные ситуации, причем равновесные стратегии игроков одновременно являются и максиминными, а соответствующие им выигрыши равны. В неантагонистической игре ситуации (а₀,b₀) и(a*,b*)(равновесная и максиминная соответственно) в чистых стратегиях не обязательно совпадают, а попарные пересечения равновесных стратегий не обязательно образуют равновесные ситуации. В общем случае, не совпадают и величины равновесного и максиминного выигрышей: первый не меньше второго.

В то время как максиминные стратегии a*, b* игроков консервативны и обеспечивают им, возможно, и небольшой, но гарантированный результат, использование равновесных стратегийа₀,b₀, приводящих, как правило, к большему выигрышу, требует определенной доли риска.

Отмеченные обстоятельства позволяют на основе содержательного анализа принципов наибольшего гарантированного результата и равновесия рекомендовать следующие правила поведения в неантагонистической игре:

• следовать максиминной стратегии, если соответствующей ей наибольший гарантированный результат совпадает по величине с равновесным;

• следовать равновесной стратегии, если величина равновесного выигрыша превышает максиминный и есть уверенность, что противник поступит так же;

• следовать максиминной стратегии, если функция выигрыша противника неизвестна или известна лишь приближенно.

Реально ситуация равновесия (а₀,b₀) может оказаться доминируемой в том смысле, что существует некоторая ситуация(а,b) для которой выполняется условие:

причем хотя бы одно из этих неравенств строгое и, следовательно, принципы выгодности и равновесия входят в противоречие. Последнее обстоятельство вынуждает игроков отклоняться от ситуации равновесия (а₀,b₀) с целью получения больших выигрышей. Игра становится неустойчивой.

Таким образом, в качестве решения неантагонистической игры в чистых стратегиях может быть принята только недоминируемая равновесная ситуация, дающая каждому из игроков выигрыши большие, чем соответствующие максиминные результаты.

Для нахождения равновесных ситуаций можно воспользоваться определением (4.11) и сформулировать задачи параметрического программирования, решением которых будет искомая ситуация равновесия.

Биматричные игры

Рассмотрим биматричные игры. Термин "биматричная'' в названии игры объясняется тем, что на множестве ситуаций игры задается матрица, каждый из элементов которой содержит упорядоченную пару чисел(v₁(i,j), v₂(i,j)).Проводя с биматрицей линейное преобразование по правилу

h: =a(i,j) =v₁ (i,j)+h, > 0, i=1,m, j=1,n; h0,

g: =b(i,j)= v₂(i,j)+g, >0, , i=1,m, j=1,n; g 0,

получаем биматрицу с положительными элементами.

Процедура нахождения ситуации (i₀,j₀) равновесия аналогична процедуре нахождения ситуации(а₀,b₀) равновесия.

Проиллюстрируем особенности решения биматричной игры на простых гипотетических примерах.

Пример. 4.6

Рассмотрим биматрицу

.

Какие чистые стратегии предпочтительны? Для 1-го игрока предпочтительна его 1-я стратегия, которая обеспечивает выигрыш не менее 2. В этих условиях для 2-го игрока предпочтительна его 1-я стратегия, которая обеспечивает ему наибольший выигрыш, равный 3. Таким образом возникает ситуация равновесия: i₀=1 иj₀=1.

Пример 4.7

Рассмотрим матрицу

Какие чистые стратегии предпочтительны? Если 1-й игрок выберет свою 1-ю стратегию в надежде получить выигрыш, равный 3, то 2-й игрок может выбрать свою 1-ю стратегию и получить больший выигрыш, чем 1-й игрок. Если 1-й игрок выберет свою 2-ю стратегию в надежде получить выигрыш, равный 3, то 2-й игрок может перейти на свою 2-ю стратегию и снизить выигрыш 1-го игрока.

Таким образом, в этой игре нет ситуации равновесия в чистых стратегиях. Но всякая биматричная игра имеет по крайней мере одну ситуацию равновесия, возможно в смешанных стратегиях.

Пример 4.8

Реальная конфликтная ситуация характеризуется игрой, заданной матрицей

.

Первый игрок предпочитает свою 1-ю стратегию, которая может обеспечить ему максимальный выигрыш =4. Второй игрок предпочитает свою 2-ю стратегию, которая может обеспечить ему выигрыш =6. Однако если бы 1-й игрок знал о намерении 2-го игрока, он предпочел бы выбрать свою 2-ю стратегию и довольствоваться выигрышем =3. Если же 2-й игрок узнает о намерении 1-го игрока, то он перейдет на свою 1-ю стратегию и получит выигрыш 3, оставив 1-го игрока без выигрыша вообще.

Итак, интересы игроков не совпадают. Значит, ситуация равновесия отсутствует. Следовательно, решение игры нужно искать в смешанных стратегиях, если, конечно, платежи в матрице - количественные оценки предпочтительности.

Рассмотрим варианты принятия решений в зависимости от соотношений максиминных и равновесных выигрышей участников.

Случай 1. Оба игрока применяют свои максиминные стратегии.

Максиминная смешанная стратегия 1-го игрока определяется путем решения уравнения

Откуда р*=0,5.

Исход игры:

Максиминная смешанная стратегия 2-го игрока определяется путем решения уравнения

или

откуда q*=5/6.

Исход игры

Случай 2. Оба игрока применяют свои равновесные стратегии.

Равновесной смешанной стратегией одного игрока является такая, при которой средний выигрыш другого игрока не зависит от применяемой им стратегии.

Первый игрок должен выбрать такую стратегию, чтобы при любой стратегии 2-го игрока тот получил одинаковый выигрыш. Для этого должно выполняться условие

или

откуда р⁰=1/3.

Тогда выигрыш 2-го игрока .

Аналогично 2-й игрок должен выбрать такую стратегию, чтобы при любой стратегии 1-го игрока тот получил одинаковый выигрыш. Для этого должно выполняться условие

или

откуда q⁰ =1/3.

Тогда выигрыш 1-го игрока

Таким образом, выигрыши игроков в максиминной и равновесной ситуациях

совпадают:

Случай 3. Один игрок применяет максиминную, а другой - равновесную стратегию.

Если 1-й игрок применяет свою равновесную стратегию, а 2-й игрок - свою максиминную, выигрыши игроков определяются следующим образом.

Для 1-го игрока:

или

Для 2-го игрока:

или

Если 1-й игрок применяет свою максиминную стратегию, а 2-й - свою равновесную, выигрыши игроков определяются следующим образом.

Для 1-го игрока:

или

Для 2-го игрока:

или

Выигрыши игроков при применении ими максиминных или равновесных стратегий сведены в следующую таблицу:

Стратегия 1-го игрока	Стратегия 2-го игрока
	Максиминная	Равновесная
Максиминная	(2 ; 2,667)	(2 ; 3,167)
Равновесная	(1,5 ; 2,667)	(2;2,667)

Анализ данных таблицы позволяет сделать следующий вывод: 1-му игроку целесообразно придерживаться максиминной стратегии, а 2-му - равновесной.

Пример 4.9

Рассмотрим биматричную игру, получившую наименование семейный спор. Она достаточно адекватно моделирует договорной процесс о разделе сфер влияния в сегменте рынка. Каждая из сторон предлагает свой вариант раздела сегмента рынка, который, разумеется, более предпочтителен для нее. И каждая из сторон может или жестко настаивать на своем варианте (это стратегии i₁ и j₁ соответственно), или согласиться на вариант, предлагаемый конкурентом (стратегии i₁ и j₂ соответственно).

Матрица игры имеет вид:

.

Если конкуренты не договорятся и каждый будет настаивать на своем варианте раздела, то их реальные выигрыши составят =0;=0;=0;=0.

Здесь две ситуации равновесия - (1;2) и (2;1). Первая ситуация равновесия выгодна 1-му игроку, а вторая - 2-му игроку.

Решение игры определяется готовностью одного из игроков уступить другому или компромиссным решением о разделе сфер влияния.

Пример 4.10

Рассмотрим биматричную игру, получившую в теории наименование дилемма заключенных. Она может быть рекомендована для моделирования процесса достижения договоренности об исключении протекционизма и диктата на рынке.

Выигрыши заданы в полезностях. Биматрица игры имеет вид:

.

Игроки могут оба задействовать рычаги давления и "насмерть бороться" друг с другом, используя антирыночные механизмы (ситуация (i₁ ,j₁)). Это наименее выгодная и им и обществу ситуация, приносящая незначительную выгоду, например по три единицы полезности каждой из сторон. Если оба игрока откажутся от протекционизма и не будут нарушать принципов конкуренции (ситуацияi₂, j₂)), то это приведет к экономическому подъему и существенному приросту прибылей - втрое для каждой стороны. Если же после достижения договоренности какая-то из сторон тайно нарушит условия договора, а вторая по-прежнему будет его исполнять, то это резко изменит соотношение в полезностях: сторона, сохраняющая верность договору, все потеряет, а нарушившая договор - станет монополистом (на это указывает существенная асимметрия величин полезностей в ситуациях ((i₂, j₁) и (i₁, j₂) соответственно). Здесь имеется единственная ситуация равновесия (1,1). Она дает каждому игроку скромный выигрыш, равный 3. Для этого оба должны придерживаться протекционизма, то есть выбрать каждый свою 1-ю стратегию. Однако эта ситуация доминируется ситуацией (2,2), которая выгоднее обоим игрокам, при условии, если каждый откажется от протекционизма. Но раз существует опасность "предательства" (тайного выхода из договора), это делает ситуацию (2,2) неустойчивой.

Таким образом, решение игры определяется морально-этическими качествами договаривающихся сторон. Но в этом нет ничего удивительного, ведь все блага, которые дает цивилизация, вытекают исключительно из цивилизованных отношений сторон. Подобные отношения всегда выгодны только в том случае, когда каждый из взаимодействующих в обществе субъектов сознательно принимает для себя некие правила поведения, ограничения и мораль, когда воля отдельного индивида подчиняется воле всего цивилизованного общества.

Методы принятия решений в условиях природной неопределенности

Рассмотрим теперь основные критерии выбора решений в условиях природной неопределенности (игра с природой) применительно к простейшему случаю, когда результат скалярный и его желательно максимизировать. В зависимости от типа отношения ЛПР к риску гарантированный результат формируется по-разному, и это определяет вид критерия.

Если ЛПР при выборе решения абсолютно не приемлет риска (абсолютно не склонен к риску), то оно всегда предпочитает ориентироваться на самые небла­гоприятные значения состоянийs природы. В этом случае гарантированный результат определяется функцией.

Наилучшей стратегией будет та, которая обеспечивает наибольший из гарантированных результатов для всех возможных стратегий. Таким образом, крите­рий выбора для ЛПР, абсолютно не склонного к риску, имеет вид:

. (4.12)

Критерий (4.12) был предложен Вальдом, и поэтому часто его связывают с этим именем. Другое название критерия - максиминный критерий обусловлено видом выражения (7.12).

Для использования этого принципа достаточно, чтобы шкала показателя

у была хотя бы порядковой.

Пример.

Значения показателя эффективности для трех стратегий и трех значении неопределенного фактора представлены в следующей таблице.

А	S
	s1	s2	s3
a1	8	8	2	2
a2	3	13	1	1
а3	5	15	0	0

Тогда оптимальной стратегии соответствует значение показателя эффективности y(a*)=2.

Максиминный критерий ориентирован на наихудшие значения неопределенного фактора и в этом смысле является чрезвычайно консервативным. Поэтому его следует применять в тех случаях, когда неуспех операции крайне нежелателен, независимо от того, какими могут быть другие (благоприятные) исходы операции.

Если для ЛПР небезразлична величина возможного выигрыша (то есть оно боится мало выиграть), то в качестве гарантированного результата для стратегии ЛПР можно использовать, например, величину

Предложивший это выражение для гарантированного результата исследователь Сэвидж назвал его "сожалением", что и определило наименование критерия выбора - "критерий минимаксных сожалений". Этим критерием обычно руководствуется ЛПР, склонное к риску. Лучшая стратегия определяется правилом

(4.13)

В условиях рассмотренного примера матрица сожалений может быть определена, если в каждом столбце вычислить разности между наилучшим текущими значениями показателя. В результате получим следующую матрицу сожалений:

А	S
	s1	s2	s3
a1	0	7	0	7
a2	5	2	1	5
а3	3	0	2	3
				3

Оптимальная стратегия а* = а₃.

Одним из существенных недостатков принципа Сэвиджа является то, что добавление новой, заведомо неоптимальной стратегии может сделать неоптимальной полученную ранее оптимальную стратегию.

Максиминный критерий и критерий Сэвиджа являются слишком категоричными в том смысле, что один ориентируется не только на наихудший результат, другой - на максимальные потери ("сожаления").

Если ЛПР боится не только мало выиграть, но и много проиграть, то его отношение к риску можно охарактеризовать как некоторый баланс между наилучшим и наихудшим для данной стратегии результатом. Критерий, учитывающий это обстоятельство и измеряющий два полярных исхода как некоторую линейную комбинацию, предложил Гурвиц. Согласно этому критерию лучшей следует считать ту стратегию, которая приводит к наибольшему значению линейной свертки наихудшего и наилучшего для каждой Стратегии результата:

(4.14)

причем коэффициент (его значение выбирается из интервала[0,1]) был назван Гурвицем коэффициентом оптимизма-пессимизма.

Для иллюстрации работы метода выберем те же исходные данные, что и в примере 7.11.

Пусть ЛПР задало значение показателя пессимизма - 0,75.

А	S			Значение критерия
	s1	s2	s3
a1	8	8	2	3,5
a2	3	13	1	4.0
а3	5	15	0	3.75
W(a*) =				4,0

Оптимальная стратегия а* = а₂.

Очевидно, если =0, то модель выбора по правилу(7.14) отражает предпочтения ЛПР, руководствующееся правилом "в ходе операции все сложится самым удачным образом" (крайний оптимист); если=1, то критерий Гурвица вырождается в максиминный критерий и моделирует крайне пессимистичное отношение ЛПР к возможным условиям проведения операции.

Выбор значения коэффициента может быть осуществлен одним из двух способов. Во-первых, можно предложить ЛПР эвристически назначить число из интервала [0,1] (произвести точечное оценивание параметра), которое, по его мнению, в наибольшей степени отражает баланс между оптимизмом и пессимизмом. Во-вторых, оценку можно получить из условия эквивалентности двух гипотетических ситуаций выбора, показанных на рис. 7.9.

Рис. 4.9. Ситуация выбора

При этом через у⁺ и обозначены наилучшее и наихудшее значение результата для игры с природой соответственно, a s₁ и s₂ - соответствующие им состояния природы. Запись s₁s₂ означает, что результат Y получается вне зависимости от того, какое из двух состояний природы реализуется, то есть наверняка.

ЛПР должно указать такое значение значение Y результата, что ему будет безразлично, получить ли его наверняка или принять участие в игре с природой с двумя возможными исходами - наилучшим и наихудшим. После получения величиныYсоставляется очевидное равенство,

из которого следует, что

.

Заметим, что критерий Гурвица может не различать явно различающиеся по предпочтительности альтернативы в силу того, что каждой из них ставит в соответствие оценку, являющуюся линейной комбинацией наихудшего и наилучшего результата для этой альтернативы.

Дня устранения отмеченного недостатка критерий Гурвица желательно модифицировать таким образом, чтобы помимо крайних по предпочтительности значений результата в нем фигурировали и промежуточные результаты при оценке каждой альтернативы.

Об одной из таких модификаций критерия Гурвица, а также о некоторых других критериях выбора в условиях природной неопределенности один из авторов данного пособия, С. Н. Воробьев, подробно рассказал в статье. В этой статье, в частности, отмечено, что использование классических критериев Вальда, Сэвиджа, Гурвица, Бернулли) во многом затруднено из-за того, что они достаточно скромно отражают все многообразие психофизических характеристик личности ЛПР, а описания этих критериев фактически не содержат практических рекомендаций, к какому типу личности ЛПР тот или иной критерий лучше применять.

Во многом это обстоятельство как раз и было обусловлено тем (об этом мы упоминали), что само слово "риск" традиционно связывалось с неопределенностью только стохастического характера. Автор ввел понятие риска для случая природной неопределенности, определив риск как "плату" за возможность получения наиболее благоприятного исхода в операции.

Таким образом, в качестве наказания за принятие рискованного решения выступает угроза получения неблагоприятного исхода. В соответствии с таким оп­ределением риск можно оценивать, например, величиной разности между наиболее и наименее предпочтительными результатами для каждой из возможных стратегий или величиной разности между текущими результатами и уровнем притязаний. Под уровнем притязаний автор предложил понимать любой результат, достижение которого отождествляется в сознании ЛПР с конечным успехом.

Это подтвердилось многочисленными практическими наблюдениями за процессом принятия решений: очень часто при принятии решений в условиях природной неопределенности респонденты оценивали уровень притязаний как самый лучший результат из возможных при данных обстоятельствах, как некоторый вполне конкретный результат между худшим и лучшим при данных обстоятельствах или даже любой не самый худший.

Применительно к задачам принятия решений и условиях неопределенности было дано определение "тип личности ЛПР" по его отношению к степени возможности различных (благоприятных и неблагоприятных) состояний природы и понятие "склонность к нестохастическому риску".

В результате стали различать следующие "типы личности" ЛПР:

• "пессимист" - субъект, который при принятии решений в условиях неопределенности всегда руководствуется следующим внутренним убеждением: "если неприятности могут произойти, то со мной они произойдут обязательно";

• "реалист" - руководствуется установкой: "при проведении операции благоприятные и неблагоприятные состояния природы имеют примерно одинаковую степень возможности";

• "оптимист" - всегда руководствуется правилом: "со мной все будет хорошо, и все сложится удачно".

Кроме того, для "пессимиста" и "оптимиста" были выделены две дополнительные градации: "крайний..." и "разумный...".

Характер отношения ЛПР к риску в условиях природной неопределенности автор определил через его готовность пойти на возможность получения наихудшего для данной стратегии результата в надежде получить лучший результат. На этой основе были предложены следующие характеристики отношения ЛПР к нестохастическому риску:

• "несклонный к риску" - это ЛПР, которое "боится много проиграть", и поэтому при оценке возможных стратегий в первую очередь обращает внимание на величины связанных с ними наихудших результатов;

• "склонный к риску" - это ЛПР, которое "боится мало выиграть", и поэтому при оценке возможных стратегий в первую очередь обращает внимание или на величины связанных с ними наилучших результатов, или на величины "сожалений", вычисляемых для каждой возможной ситуации как разность между наилучшим при данном состоянии природы результатом и всеми текущими для него;

• "безразличный к риску" - это ЛПР, которое придает одинаковый вес как: наи­лучшим, так и наихудшим результатам, учитывая возможные промежуточные результаты.

После такого определения "типа личности" ЛПР и введения градаций его отношения к нестохастическому риску осталось только применить метод морфологических таблиц и сформировать систему почти из 20 критериев, в которую, конечно же, вошли и все классические критерии выбора.