Задание №18

№ вар.

Решить методом потенциалов транспортную задачу, заданную матрицами: А - запасов; В - потребностей; С - тарифов.

№ вар.

I

II

III

IV

V

VI

VII

VIII

IX

X

Ответ для "Z_опт":

1. 965;

2. 320;

3. 287;

4. 215;

5. 214;

6. 210;

7. 190;

8. 162;

9. 80;

10. 42;

11. Не знаю.

№ вар.

Построить математическую модель транспортной задачи и найти ее решение методом потенциалов.

I

Составить план перевозок каменного угля с трех шахт в четыре пункта. Производительность шахт (тыс.т) равна соответственно 100; 150; 50. Потребности заказчиков равны: 75; 80; 60; 85 тыс. т. Стоимость перевозки одной тонны угля задается элементами матрицы

.

Составить план перевозки, обеспечивающий минимальные транспортные издержки.

II

Три совхоза выделяют соответственно 40; 50; 30 ц молока для ежедневного снабжения четырех пунктов, потребности которых составляют соответственно 20; 40; 30; центнеров молока. Стоимости перевозок 1 ц молока задаются матрицей

.

Организовать снабжение так, чтобы потребители были обеспечены молоком, а транспортные расходы были минимальны.

III

В четырех хранилищах имеются соответственно 40; 50; 60 и 30 т топлива. Требуется спланировать перевозки так, чтобы спрос трех потребителей, составляющий соответственно 60; 80; 40 т, был удовлетворен, а затраты на транспортировку были минимальны. Стоимость перевозок 1 тонны топлива задаются матрицей

.

IV

С четырех складов, где хранится соответственно 50; 160; 70; 100 т картофеля, необходимо вывезти его в пять торговых точек. Объем завоза составляет соответственно 80; 100; 90; 50; 60 тонн. Стоимости перевозок 1 т картофеля задаются матрицей

.

Закрепить поставщиков за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной.

V

Товары с четырех баз поставляются в четыре магазина. Запасы товара на базах составляют 40; 60; 40; 80 тысяч единиц. Потребности магазинов равны (тыс. ед.) 30; 80; 60; 50. Затраты на перевозку 1 тысячи единиц заданы матрицей

.

Спланировать перевозки так, чтобы полностью удовлетворить потребности магазинов, а затраты на перевозку свести к минимуму.

VI

Продукцию трех заводов (тысячи единиц) 40; 50; 30 соответственно необходимо доставить потребителям, спрос которых составляет 20; 50; 45; 30 тысяч единиц. Известна матрица транспортных расходов:

.

Составить план перевозок так, чтобы суммарные транспортные расходы были минимальны.

VII

Найти оптимальный план перевозок по данным задачи VI варианта при дополнительном условии обязательного полного удовлетворения спроса второго потребителя b₂ = 50 тыс.ед.

VIII

Собранный урожай зерна в четырех совхозах должен быть перевезен на три элеватора, мощности которых составляют соответственно 90; 70; 50 тысяч тонн. Составить план перевозки зерна, минимизирующий транспортные расходы, если урожай по совхозам составил (тыс.т): 50; 60; 70; 40. Известна матрица транспортных расходов:

.

IX

Заводы №1, 2, 3 производят однородную продукцию в количестве соответственно 490; 450 и 470 единиц. Продукция отправляется в три пункта, потребности которых равны соответственно 300; 340 и 360 единицам. Известна матрица транспортных расходов:

.

Организовать перевозки так, чтобы суммарная стоимость транспортных расходов была минимальной, при условии, что коммуникации между заводом №2 и первым пунктом не позволяют пропускать в рассматриваемый период более 200 единиц продукции.

X

Найти оптимальное распределение трех видов механизмов, имеющихся в количестве 45; 20 и 35, между четырьмя участками работ, потребности которых составляют соответственно 10; 20; 30; 40 механизмов при следующей матрице производительности каждого из механизмов на соответствующем участке работы:

.

Нулевые элементы означают, что данный механизм не может быть использован на данном участке работы.

Ответ:

"Z_min"

1. 2618;

2. 1640;

3. 1020;

4. 805;

5. 565;

6. 560;

7. 528;

8. 460;

9. 451;

10. 296.
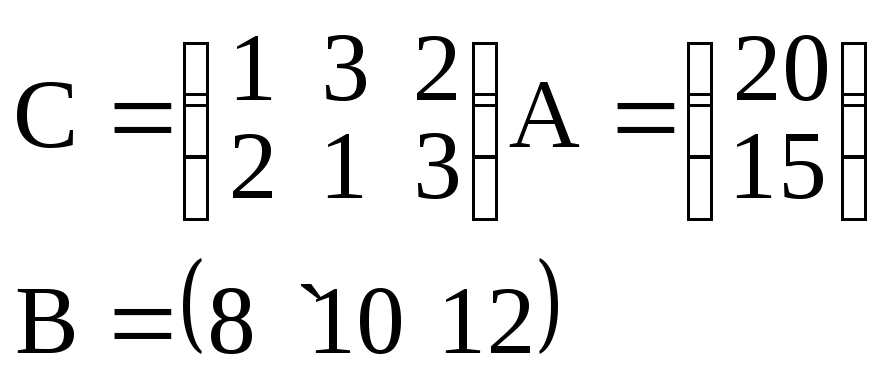
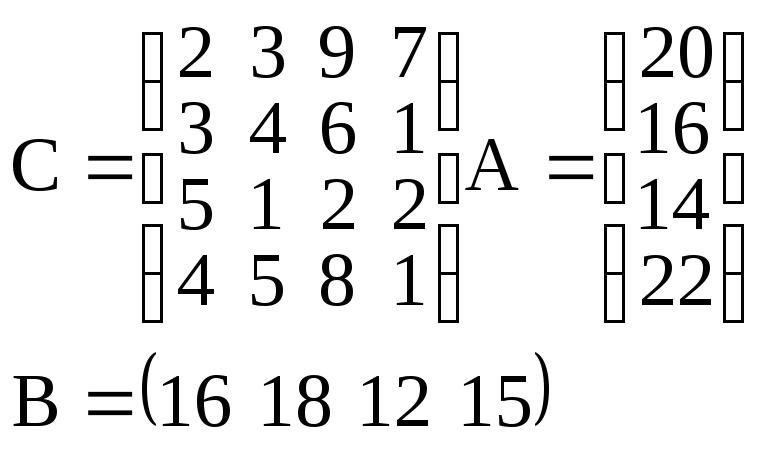