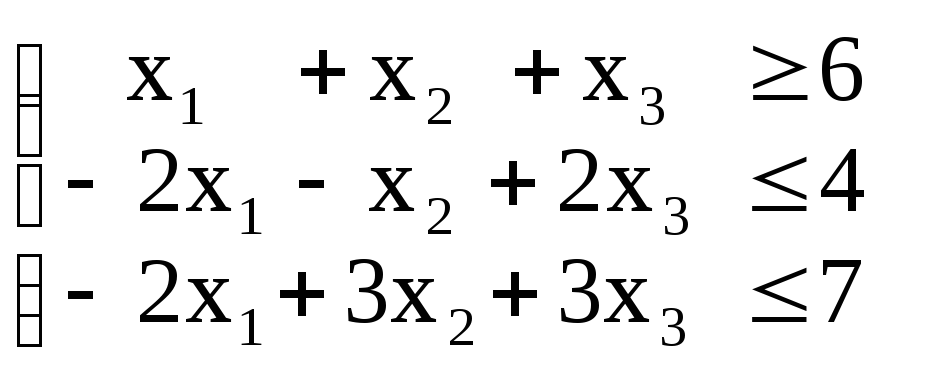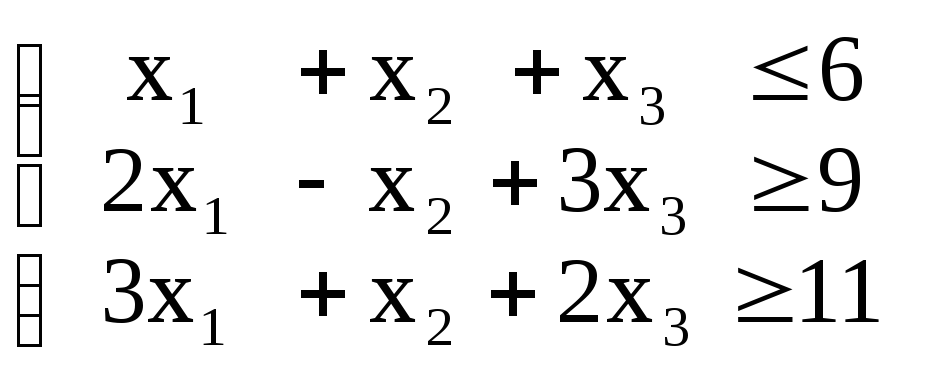Задание №14

№ вар.

А. Определить, является ли указанный вектор оптимальным решением данной задачи;

Б. Решив двойственную к данной графически, найти решение исходной.

№ вар.

I

Z = x₁ + 8x₂ + 10x₃ max

x_1,2,3  0; =(1,0,0)

Z = x₁ + 4x₂ + x₃ max

x_1,2,3  0; =(0,1/2,1/2)

II

III

Z = x₁ + x₂ + x₃ max

x_1,2,3  0; =(1,0,0)

Z = x₁ + x₂ + x₃ min

x_1,2,3  0; =(1,0,1)

IV

V

Z = ‑4x₁ ‑ 3x₂ ‑ 2x₃ ‑ 5x₄ max

x_1,2,3,4  0; =(0,2,2,0)

Z = x₁ ‑ 3x₂ + x₃ max

x_2,3  0; =(2,1,0)

VI

VII

Z = 2x₁ + 3x₂ ‑ 7x₃ + 14x₄ max

x_1,2,3,4  0; =(0,1,1,0)

Z = x₁ + x₂ ‑ 2x₃ ‑ 3x₄ max

x_3,4  0; =(-1,-2,0,0)

VIII

IX

Z = x₁ + x₂ ‑ 4x₃ max

x_1,2,3  0; =(1,0,1)

Z = x₁ + x₂ +x₃ min

x_1,2,3  0; =(1,1,0)

X

Ответ для "А":

1. Да; 2. Нет; 3. Не знаю.

Ответ для "Б" (решение двойственной):

1.Y₀ = (-5/2,1/2);

2. Y₀ = (-1/3,5/3);

3. Y₀ = (0,1);

4. Y₀ = (5/18,13/18);

5. Y₀ = (2/7,1/7);

6. Y₀ = (2/5,-1/5);

7. Y₀ = (5/4,-1/4);

8. Y₀ = (3/2,-1/2);

9. Y₀ = (9/2,-7/2);

10. Y₀ = (13,-11);

11. Не знаю.

№ вар.

Построить двойственную задачу к данной. Решив одну из них, найти оптимальное решение другой любым известным способом. (все x_j  0, )

№ вар.

I

Z = 4x₁ + 3x₂ + 5x₃ max

Z = 2x₁ + 3x₂ + 4x₃ max

II

III

Z = ‑2x₁ + 3x₂ + x₃ max

Z = x₁ + 3x₂ ‑ x₃ +2x₄ min

IV

V

Z = x₁ + 2x₂ + x₃ ‑ 3x₄ max

Z = ‑3x₁ + x₂ ‑ 3x₃ ‑ 2x₄ max

VI

VII

Z = 3x₁ ‑ 2x₂ ‑ x₃ min

Z = 5x₁ + 4x₂ + 6x₃ max

VIII

IX

Z = 2x₁ + 3x₂ + x₃ +x₄ min

Z = 4x₁ + 3x₂ +4x₃ + x₄ ‑x₅ max

X

Ответ для "Z_опт":

1. 95;

2. 40;

3. 38;

4. 68/3;

5. 21;

6. 7;

7. 5;

8. 4;

9. ‑1/7;

10. ‑5;

11. Не знаю.

№ вар

Построить двойственную задачу к данной. Решить одну из пары задач, найти оптимальное решение другой. Проверить выполнение теорем двойственности.

№ вар

Ax₁+x₂+8x₃→max

A

B

C

A

B

C

1

4/3

4

5

7/3

4

3

11

2

3/2

6

4

19/5

6

2

12

3

7/3

2

3

3/2

2

4

13

4

6/5

3

6

5/3

6

5

14

5

5/4

2

7

7/2

5

2

15

6

3/4

4

6

3/2

2

5

16

7

16/5

3

2

7/4

5

4

17

8

6/5

2

6

15/4

7

2

18

9

9/5

3

4

4/3

5

6

19

10

7/2

4

2

7/3

6

3

20

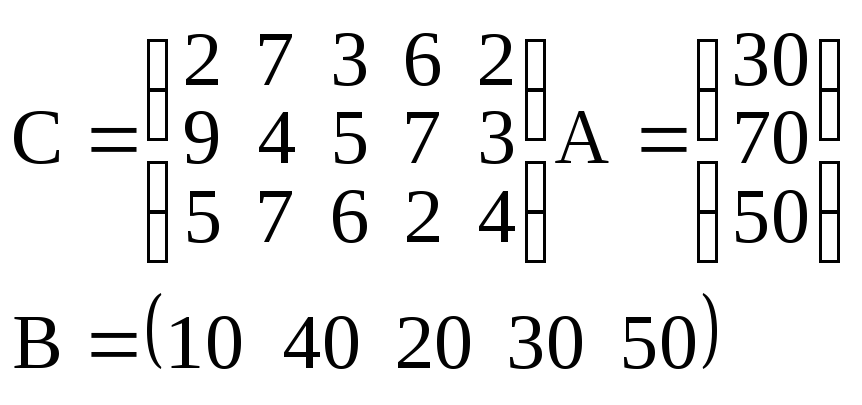
№ вар.

Решить методом потенциалов транспортную задачу, заданную матрицами: А - запасов; В - потребностей; С - тарифов.

№ вар.

I

II

III

IV

V

VI

VII

VIII

IX

X

Ответ для "Z_опт":

1. 930;

2. 690;

3. 665;

4. 518;

5. 495;

6. 470;

7. 435;

8. 240;

9. 215;

10. 190;

11. Не знаю.