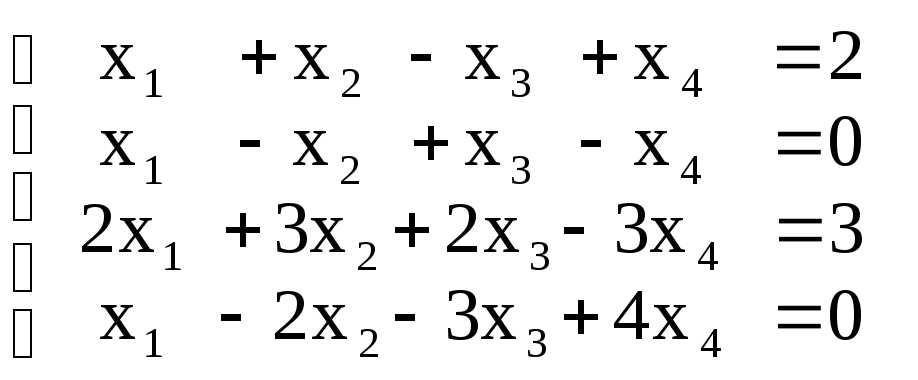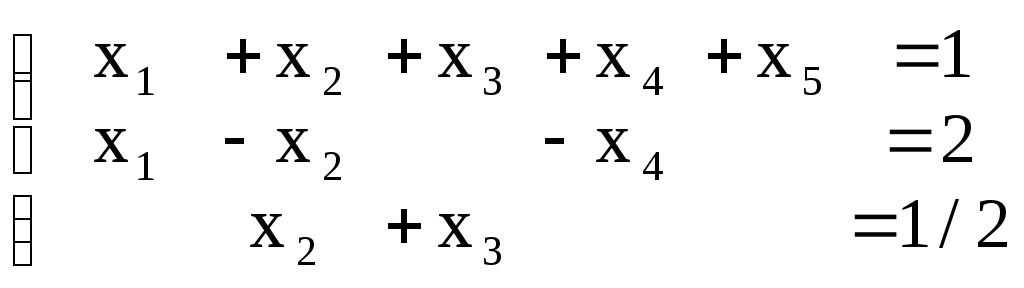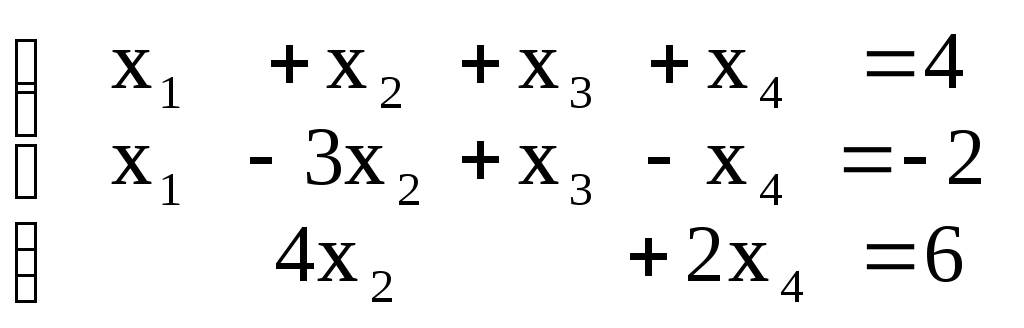Задание №6

№ вар.

Решить задачу симплекс-методом.

(Все x_j  0).

№ вар.

I

Z = x₁ + x₂ + x₃ + x₄ max

Z = x₁ + x₂ ‑ x₃ + 5x₄ max

II

III

Z = 3x₁ + 2x₂ + x₃ + x₄ ‑ 5x₅ ‑ 10x₆ max

Z = x₁ + x₂ + x₃ ‑x₅ max

IV

V

Z = x₁ ‑ x₂ + x₃ ‑ x₄ + x₅ ‑ x₆ max

Z = x₁ + 2x₂ + x₃ ‑ 2x₄ + x₅ ‑2x₆ max

VI

VII

Z = x₁ + 2x₆ max

Z = x₁ ‑ 2x₂ + 2x₃ + 3x₄ ‑ x₅ min

VIII

IX

Z = x₁ + x₂ + x₃ ‑ x₅ min

Z = x₁ ‑ x₂ + 2x₃ ‑ x₄ + x₅ min

X

Ответ:

1.Одно решение.

3.Неограниченная.

5.Не знаю.

2.Множество решений.

4.Несовместная система.

№ вар.

Решить задачу симплекс-методом (все x_j  0).

Записать общее оптимальное решение.

Найти компоненты оптимального решения при условии:

,

№ вар.

I

Z = x₁ + x₂ + x₃ max

Z = x₁ + x₂ + x₃ min

II

III

Z = 2x₁ + 3x₂ ‑ 6x₃ + 8x₄ + 10 min

Z = x₁ ‑ 3x₂ + x₃ ‑x₄ min

IV

V

Z = x₁ + 2x₃ + 2x₅ max

Z = ‑x₁ ‑ x₂ + x₃ max

VI

VII

Z = x₁ ‑ 4x₂ + 2x₃ min

Z = x₁ + x₂ + x₃ + 3x₄ +x₅ max

VIII

IX

Z = x₁ + x₂ + x₃ max

Z = x₁ + 2x₃ + 2x₅ min

X

Ответ:

"Z"

1

2

3

4

5

6

7

8

9

‑2

1

2

3

4

6

10

12

Не знаю

"X_опт"

1.(0,3/4,5/4,0).

3.(2/3,2/3,0/1).

5.(1/2,1,1/2,0).

7.(7/8,3/4,7/8,3/4).

9.(1/3,3,0,1/4,5/4).

11.Не знаю.

2.(1/2,0,1/2,0).

4.(5/4,3/2,5/4,0).

6.(3/10,1/5,1/5,0).

8.(3/2,0,3/2,5/4,3/4).

10.(1,3,5,1,0).