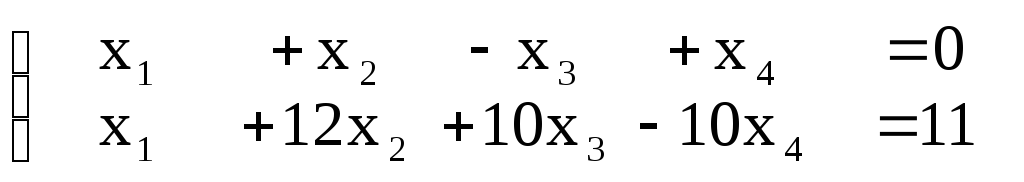Задание №4
Решить задачу, используя симплекс-метод:
Max z=х1+х2+х3-3х4
х1+Ax2+х3-3х4 ≤ 3
х1-Bх2-х3+Cx4=1
хI>=0 ,i=1..5
|
№ вар |
A |
B |
C |
№ вар |
A |
B |
C |
|
1 |
-1 |
5 |
2 |
11 |
2 |
1 |
-3 |
|
2 |
0 |
1 |
2 |
12 |
-3 |
-2 |
1 |
|
3 |
-1 |
0 |
-3 |
13 |
0 |
2 |
-3 |
|
4 |
6 |
1 |
-2 |
14 |
-1 |
2 |
1 |
|
5 |
4 |
2 |
3 |
15 |
-5 |
3 |
-3 |
|
6 |
0 |
2 |
3 |
16 |
-2 |
1 |
2 |
|
7 |
-2 |
-1 |
1 |
17 |
2 |
3 |
1 |
|
8 |
-6 |
2 |
3 |
18 |
-1 |
3 |
-5 |
|
9 |
2 |
-1 |
3 |
19 |
2 |
1 |
5 |
|
10 |
-4 |
1 |
-4 |
20 |
3 |
-4 |
1 |
Решить задачу, используя симплекс-метод:
Max z=-2x1+x2-7x3+Ax4+3x5
3x1+x2+2x3+Bx4+4x5 ≤ 15
-x1+Cx2-x3+2x4-x5=-4
xi>=0, i=1..5
|
№ вар |
A |
B |
C |
№ вар |
A |
B |
C |
|
21 |
1 |
-1 |
1 |
31 |
2 |
-5 |
-2 |
|
22 |
0 |
-7 |
1 |
32 |
-1 |
-6 |
-3 |
|
23 |
2 |
-1 |
1 |
33 |
1 |
-5 |
2 |
|
24 |
1 |
-1 |
-1 |
34 |
6 |
-7 |
3 |
|
25 |
1 |
-5 |
-2 |
35 |
2 |
-5 |
2 |
|
26 |
1 |
-7 |
2 |
36 |
3 |
-1 |
-1 |
|
27 |
2 |
-1 |
-1 |
37 |
-2 |
-8 |
1 |
|
28 |
1 |
2 |
1 |
38 |
-1 |
-6 |
3 |
|
29 |
5 |
-6 |
1 |
39 |
3 |
-5 |
-2 |
|
30 |
3 |
-1 |
1 |
40 |
7 |
-6 |
2 |
Задание №5
|
№ вар. |
Решить задачу max и min симплекс-методом. (Все xj 0). |
№ вар. |
|||||||||||||||||||
|
I |
Z = 2x1 + 4x2
|
Z = x1 + x2 + x3
|
II |
||||||||||||||||||
|
III |
Z = x1 + x2
|
Z = x1 + x2 + x3
|
IV |
||||||||||||||||||
|
V |
Z = x1 ‑ 4x2 + 3x3 + 10x4
|
Z = x1 ‑ 8x2 + x3 + 4x4
|
VI |
||||||||||||||||||
|
VII |
Z = x1 ‑ x2 + 3x3
|
Z = x1 ‑ 4x2 + 3x3 + 10x4
|
VIII |
||||||||||||||||||
|
IX |
Z = x1 ‑ 4x2 + 4x3
|
Z = x1 + x2 + x3
|
X |
||||||||||||||||||
|
Ответы: |
1.Zmax - одно решение; 2. Zmax - одно решение; 3.Zmax - не ограничена; 4.Zmax - не ограничена; 5.Система несовместна. 6.Не знаю. |
Zmin - одно решение. Zmin - не ограничена. Zmin - одно решение. Zmin - не ограничена. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
"Z" |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
||||||||||||
|
|
‑7 |
‑1/2 |
0 |
1 |
4 |
10 |
Не знаю |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
