Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ижевский государственный технический университет им. М. Т. Калашникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

8-12_BM

.odt

Скачиваний:

Добавлен:

12.03.2015

Размер:

31.14 Кб

Скачать

☆

8.Необходмое условие существования предела последовательности. ( критерий Коши)

Для того чтобы последовательность сходилась необходимо и достаточно, чтобы N .

А также два достаточных признака:

Теорема 2. Если последовательность монотонно возрастает и ограничена сверху, то она сходится. (Аналогичный признак для монотонно убывающей и ограниченной снизу последовательности)

Единственность предела последовательности.

Теорема: ( о единственности предела последовательности )

Числовая последовательность может иметь только один предел.

Доказтельство:

Предположим, что последовательность $X_{n}$ имеет два различных предела b и a, причем b < a.

Выберем $\varepsilon > 0$ таким, чтобы $\varepsilon$ -oкрестности точек b и a не пересекались (не имели общих точек). Возьмем, например, $\varepsilon = \frac{(a-b)}{3}$ . Так как число b — предел последовательности $X_{n}$ , то по заданному $\varepsilon > 0$ можно найти номер N такой, что $X_{n}\in U_{\varepsilon }(b)$ для всех $n\geq N$ . Поэтому вне интервала $U_{\varepsilon }(b)$ может оказаться лишь конечное число членов последовательности. В частности, интервал $U_{\varepsilon }(a)$ может cодержать лишь конечное число членов последовательности. Это противоречит тому, что a — предел последовательности (любая окрестность точки a должна содержать бесконечное число членов последовательности). Полученное противоречие показывает, что последовательность не может иметь два различных предела. Итак, сходящаяся последовательность имеет только один предел.

9.Определение бесконечно малой последовательности

Последовательность $\left \{ \alpha_{n} \right \}$ называется бесконечно малой, если $\lim\limits_{n \rightarrow \infty }\alpha_{n} =0$ , т.е. $\forall \varepsilon >0 \;\; \exists N_{\varepsilon}>0 \;\;\forall n\geq N_{\varepsilon} \;\;|\alpha_{n}|<\varepsilon$ .

Свойства бесконечно малых последовательностей

Бесконечно малая последовательность ограничена.
Сумма бесконечно малых последовательностей есть бесконечно малая последовательность.
Произведение бесконечно малой последовательности на ограниченную есть бесконечно малая последовательность.
Если элементы бесконечно малой последовательности $\left\{\alpha_{n}\right\}$ равны одному и тому же числу ,

то .

Основные теоремы о бесконечно малых последовательностях

Теорема 1. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.

Доказательство. Пусть – бесконечно малая последовательность. Это означает, что для любого положительного числа существует такой номер N, что для всех номеров выполняется условие , где С – любое действительное число. Тогда <

< , а это и означает, что последовательность – бесконечно малая.

Теорема 2. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство. Пусть и – бесконечно малые последовательности. Это означает, что для любого числа существуют такие номера и , что для всех номеров и для всех номеров выполняются условия и соответственно. Тогда для всех номеров выполняется условие, а это и означает, что последовательность – бесконечно малая.

Следствие 1. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Следствие 2. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 3. Бесконечно малая последовательность ограничена.

Доказательство. Пусть – бесконечно малая последовательность, ε>0 – некоторое число, а N – номер, начиная с которого выполняется условие . Обозначим через М наибольшее из следующих чисел . Очевидно, что для любого номера n, а это и означает, что последовательность {} – ограничена.

Теорема 4. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Доказательство. Пусть – ограниченная, а – бесконечно малая последовательности. Это означает, что существует число М>0 такое, что для любого номера n выполняется , и для любого числа существует номер N такой, что для всех номеров выполняется . Тогда для всех номеров и любого ε>0 выполняется , а это и означает, что последовательность – бесконечно малая.

Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 5. Если элементы бесконечно малой последовательности равны одному и тому же числу С, то С=0.

Доказательство. Предположим, что . Для существует такой номер N, что для всех номеров выполняется . Так как , а , то последнее неравенство имеет вид , откуда . Полученное противоречие показывает, что предположение неверно, следовательно, .

Теорема 6. Если – бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность , которая является бесконечно малой. Если не все элементы бесконечно малой последовательности равны нулю, то последовательность бесконечно большая.

Доказательство. Пусть – бесконечно большая последовательность. Это означает, что для любого положительного числа М можно указать такой номер N, что для всех номеров выполняется . А это означает, что при все элементы , а поэтому последовательность имеет смысл с номера N. Пусть - любое положительное число. Для числа можно указать номер такой, что для nN выполняется . Это и означает, что – бесконечно малая. Доказательство второй части теоремы проводится аналогично.

Рассмотрим теперь лемму, которая будет использоваться при доказательстве некоторых теорем.

Лемма. Для того чтобы число а являлось пределом последовательности , необходимо и достаточно, чтобы имел вид , n=1,2,…, где есть бесконечно малая последовательность.

Доказательство. Обозначим . Условие по определению предела равносильно тому, что для любого числа существует такой номер N, что для всех номеров выполняется неравенство , то есть , а это и равносильно тому, что .

Эта лемма показывает особую роль бесконечно малых последовательностей при изучении предела последовательности.

10.Бесконечно большие последовательности, их свойства и связь с бесконечно малыми последовательностями

Последовательность называется бесконечно большой, если , или .

Теорема (связь между бесконечно большими и бесконечно малыми последовательностями)

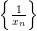Если $\left\{x_{n}\right\}$ — бесконечно большая последовательность, то начиная с некоторого номера определена последовательность $\left \{ \frac{1}{x_{n}}\right \}$ , которая является бесконечно малой.
Если все элементы бесконечно малой последовтельности $\left \{ \alpha_{n}\right \}$ отличны от нуля, то последовательность $\left \{\frac{1}{\alpha_{n}}\right \}$ — бесконечно большая.
Свойства бесконечно больших последовательностей

Сумма бесконечно больших последовательностей одного знака есть бесконечно большая последовательность того же знака.
Сумма бесконечно большой и ограниченной последовательностей есть бесконечно большая последовательность.
Произведение бесконечно больших последовательностей есть бесконечно большая последовательность.
Произведение бесконечно большой последовательности на константу есть бесконечно большая последовательность.

11.Существование предела у ограниченной монотонной последовательности.

Теорема Вейерштрасса. (Основная теорема теории последовательностей).

Если последовательность является нестрого возрастающей (нестрого убывающей) и ограничена сверху (снизу), то является сходящейся.

Данную теорему можно сформулировать немного иначе - Любая монотонная и ограниченная последовательность имеет предел.

Для того чтобы монотонная последовательность сходилась, достаточно, чтобы она была ограниченной.

Если последовательность монотонная, то для того, чтобы она была сходящейся, необходимо и достаточно, чтобы она была ограниченной.

Число е (число Эйлера)

Используя теорему Вейерштрасса, можно показать, что последовательность является сходящейся, то есть имеет предел. Данный предел равен числу е - числу Эйлера, которое является основаниемнатурального логарифма:

Док-во очень длинное, не стал сюда пихать. Делается через Бином Ньютона.

12.Геометрической прогрессией называется числовая последовательность задаваемая двумя параметрами b, q (q ≠ 0) и законом , ,

Число называют знаменателем данной геометрической прогрессии.

Если q > 0 все члены геометрической прогрессии имеют один и тот же знак, совпадающий со знаком числа b.
Если q < 0 знаки членов геометрической прогрессии чередуются.
В случае -1 < q < 1 прогрессию называют бесконечно убывающей геометрической прогрессией.

Любой член геометрической прогрессии может быть вычислен по формуле:

Формула знаменателя геометрической прогрессии:

Формула суммы n-первых членов геометрической прогрессии

где, q ≠ 1

Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q| < 1. Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма первых членов рассматриваемой прогрессии при неограниченном возрастании числа .

Формула суммы членов бесконечно убывающей геометрической прогрессии:

где, q ≠ 1

Соседние файлы в папке ВМ

#
12.03.201531.14 Кб598-12_BM.odt
#
12.03.2015211.44 Кб109Ekzamen_voprosy_po_VM_1_-_7 (1).docx
#
12.03.2015211.44 Кб111Ekzamen_voprosy_po_VM_1_-_7.docx
#
12.03.2015112.58 Кб57Ekzamen_voprosy_po_VM_31-36.docx