Матан / ЭКЗАМЕН / Матан / mat_anali_11_13_14_15

11. Предел монотонной ограниченной последовательности. Число е

Теорема Вейерштрасса

Теорема

Теорема Вейерштрасса. (Основная теорема теории последовательностей).

Если последовательность  является нестрого возрастающей (нестрого убывающей) и ограничена сверху (снизу), то  является сходящейся.

Данную теорему можно сформулировать немного иначе - Любая монотонная и ограниченная последовательность  имеет предел.

Замечание

Для того чтобы монотонная последовательность сходилась, достаточно, чтобы она была ограниченной.

Замечание

Если последовательность монотонная, то для того, чтобы она была сходящейся, необходимо и достаточно, чтобы она была ограниченной.

Применение теоремы Вейерштрасса на практике

Пример

Задание. Доказать, что последовательность  сходится.

Доказательство. Рассматриваемая последовательность ограничена снизу, так как для любого натурального  : 

Исследуем заданную последовательность на монотонность:

 ,

а значит последовательность  монотонно убывающая, а тогда, согласно теореме Вейерштрасса, последовательность сходится.

Число е (число Эйлера)

Используя теорему Вейерштрасса, можно показать, что последовательность  является сходящейся, то есть имеет предел. Данный предел равен числу е - числу Эйлера, которое является основаниемнатурального логарифма:

Пример

Задание. Найти предел последовательности  , используя тот факт, что

Решение. Приведем последовательность к соответствующему виду.

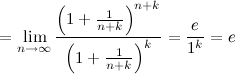
Ответ. 

13. Предел функции в точке

Пусть задано некоторое числовое множество  и каждому  поставлено в соответствие число  , тогда говорят, что на множестве  задана функция , 

Определение предела функции по Коши

Определение

Число  называется пределом функции  в точке , если для   такое, что для из того, что  следует, что  :  или при  .

Определение предела функции по Гейне

Определение

Число  называется пределом функции  в точке , если для любой последовательности , которая сходится к , соответствующая последовательность значений функции сходится к .

Полезные равенства

Теорема

Пусть функции  и  заданы в некоторой окрестности точки , кроме, возможно, самой точки , и и  . Тогда имеют место следующие равенства:

а) 

б) 

в) 

г) 

Теорема

При  функция  может иметь только один предел.

14. Предел функции при х→+∞

Бесконечно большая функция

Определение

Функция  называется бесконечно большой в точке , если для любого  существует такое, что для любого , удовлетворяющего неравенству , выполняется неравенство: . В этом случае пишут: 

Пример

Бесконечно большой функцией в точке 0 является функция 

Определение

Функция  называется бесконечно большой при , если для любого  существует такое число  такое, что для всех  из области определения функции , которые удовлетворяют неравенству , выполняется неравенство : 

Пример

Функция  является бесконечно большой функцией при .

15. Непрерывность функции в точке

Основные понятия и определения

Определение

Функция  называется непрерывной в точке , если:

1. функция  определена в точке  и ее окрестности;

2. существует конечный предел функции  в точке ;

3. это предел равен значению функции в точке , т.е. 

Замечание

При нахождении предела функции , которая является непрерывной, можно переходить к пределу под знаком функции, то есть

.

Приращение аргумента и функции

Рассмотрим функцию , которая определена в некотором интервале  и рассмотрим произвольную точку из этого интервала: .

Определение

Приращением аргумента  в точке  называется разность 

Замечание. Из последнего равенства легко увидеть, что .

Приращением функции  в точке  называется разность соответствующих значений функции  или, используя равенство из выше приведенного замечания, будем иметь:

Теорема

Функция  непрерывна в точке  тогда и только тогда, когда бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции :

Теорема

Если функции  и  непрерывны в точке , то функции , , также непрерывны в точке .

Пусть функция  задана на множестве , а  - множество значений этой функции. Пусть на множестве  задана функция . Тогда говорят, что на множестве  задана композиция функций (или сложная функция) .

Теорема

Пусть функция  непрерывна в точке , а функция  непрерывна в точке . Тогда композиция функций  непрерывна в точке .

Теорема

Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.

Точки разрыва функции и их классификация.

Определение точки разрыва

Определение

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1. функция  определена в точке и ее окрестности;

2. существует конечный предел функции  в точке ;

3. это предел равен значению функции в точке , т.е. 

называется точкой разрыва функции.

Точка разрыва первого рода

Определение

Если в точке  существуют конечные пределы  и , такие, что , то точка  называется точкой разрыва первого рода.

Точка разрыва второго рода

Определение

Если хотя б один из пределов  или  не существует или равен бесконечности, то точка называется точкой разрыва второго рода.

Точка устранимого разрыва

Определение

Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции  в точке :  или функция  не определена в точке , то точка  называется точкой устранимого разрыва.