Вопрос 24!!!

Частные и полное приращения функции двух переменных

 

Пусть задана функция z = f(х, у). Так как х и у– независимые переменные, то одна из них может изменяться, а другая сохранять постоянное значение. Дадим переменной хприращение ∆х, сохраняя значение переменной у неизменным. Тогда функцияzполучит приращение, которое назовемчастным приращением z по х и обозначим

 

∆_х z: ∆_х z = f(x + ∆x, y) – f(х, у).

Аналогично получаем частное приращениеz по у:

 

∆_у z = f(x, у + ∆ y) – f(х, у).

Наконец, если аргументу х дать приращение∆х, а аргументу у – приращение ∆у, то получим полное приращение функции z:

 

∆ z=f(x+∆x, y+∆у)–f(х, у).

Надо заметить, что полное приращение функции, вообще говоря, не равно сумме частных её приращений, т.е. ∆z ≠ ∆_х z + ∆_у z.

 

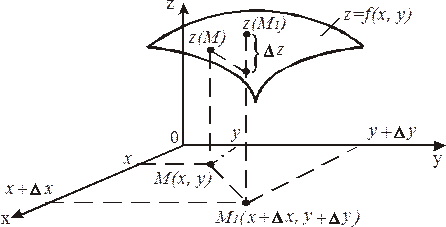
Геометрически полное приращение функции ∆z равно приращению аппликаты графика функции z = f(х, у) при переходе от точки М(х, у) к точке М₁ (х + ∆х, у + ∆у) (рис. 5).

 

 

 

         1. Частные производные первого порядка. Пусть функция  определена в области  и . Тогда при малых  определено ее частное приращение по : .

         Определение. Частной производной функции  по переменной   в точке  называют предел

,

если он существует.

         Частную производную по  обозначают одним из следующих символов:

.

Аналогично определяется частная производная по  и вводятся ее обозначения.

         Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.

         Пример. Найти частные производные функции .

 Имеем:

,    . ^

Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

Вопрос 25!!! Линии и поверхности уровня.

Рассмотрим скалярное поле, задаваемое функциейU=U(x,y,z).

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(M)принимает постоянное значение, т.е. U(x,y,z)=C (C – const).

Часто такие поверхности называются изоповерхностями.

Давая в уравнении U(x,y,z)=C величине C различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку проходит только одна поверхность уровня.

Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой круговые цилиндры, общей осью которых служит нить.

В случае плоского поля U=U(x,y,z) равенство U(x,y)=Спредставляет собой уравнение линии уровня (изолинии).

На различных картах и схемах можно найти разнообразные изолинии - линии равных глубин или высот на географических картах, линии равного давления – изобары, линии равной температуры – изотермы на метеорологических картах.

Пример: 1) Для скалярного поля U=поверхностями уровня является множество концентрических сфер с центром в начале координат

=С

 

2) Дано скалярное поле . Построить линии уровня.

 

С=1 - точка (0;0)

С=2 =3 - окружность с радиусом и центром С(0;0)

Рис. 26

С=3 =8 - окружность с радиусом и центром С(0;0) (рис. 26)