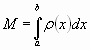Вопрос №22!!!

б) Определение определённого интеграла (слайд 4) (Определённым интегралом от функции f(x) на отрезке [a;b] называют предел интегральной суммы, когда длина максимального частичного отрезка разбиения стремится к нулю. а – нижний предел, b –верхний предел )

в) Геометрический смысл определённого интеграла (слайд 5) –

• Если f(x)?0 на [a; b] то определённый интеграл равен площади криволинейной трапеции, ограниченной линиями у=f(x), y=0, x=a, x=b.

• Если f(x)<0 на [a;b] то определённый интеграл равен взятой со знаком “минус” площади криволинейной трапеции, ограниченной линиями у=f(x), y=0, x=a, x=b.

г) С помощью какой формулы можно найти значение определённого интеграла?

 Формула Ньютона-Лейбница

2. Сегодня целью нашего урока будет посмотреть применение определённого интеграла в геометрии.

Давайте начнём с известной нам формулы площади круга. (слайд 6 -9) Рассмотрим окружность с центром в начале координат. Каким уравнением задаётся эта окружность? х²+у²=R²

Тогда её часть расположенная выше оси абсцисс есть график функции , где .

Используя геометрический смысл определённого интеграла площадь круга радиуса R

равна

Вычислим этот интеграл, пользуясь заменой переменной: .

При возрастании переменной ? что будет происходить с переменной х? возрастает от – R до R.

 и 

Тогда получим 

Как упростить подынтегральное выражение? Вынести R² за знак интеграла и воспользоваться основным тригонометрическим тождеством

, тогда 

Таким образом мы получили известную нам формулу для вычисления площади круга S=?R^2.

3. Объём тела вращения (слайд 10–11)

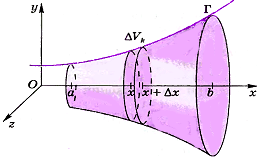
Пусть Г график непрерывной положительной функции у=f(x) в прямоугольной системе координат хОу. Необходимо вычислить объём тела вращения, ограниченного поверхностью вращения кривой Г вокруг оси х и плоскостями, проходящими через точки х = а, х = b перпендикулярно оси х. Если тело разбито на части как можно найти его объём? Объём тела равен сумме объёмов тел, его составляющих.  Поэтому можно разбить наше тело на части.

Разобьем отрезок [a;b] на части точками a<x₀<x₁<…..<x_n<b. Рассмотрим цилиндр с высотой и радиуса основания y_k = f(x_k).

Как можно вычислить объём цилиндра? 

Тогда объем нашего цилиндра будет равен 

Тогда объём всего тела может быть записан при помощи приближённого равенства . Чтобы получить точное равенство надо взять предел 

По определению определённого интеграла мы получили формулу для вычисления объёма тела вращения.

4. Решение задач

№ 1. Используя формулу объёма тела вращения, получите формулу для вычисления объёма конуса. (слайд 12)

Чтобы воспользоваться полученной формулой необходимо задать с помощью функции прямую, которую будем вращать вокруг оси Ох.

Уравнение прямой y=kx

k – угловой коэффициент прямой k=tg?=

тогда уравнение прямой примет вид 

То есть объём конуса можно вычислить по формуле 

№ 2. (самостоятельно) (слайд 13)

Вычислите объём тела, полученного вращением кривой – графика функции у= sinx, 0?х??, вокруг оси Ох.

 

№ 3 Найти объем тела, образованного вращением фигуры, ограниченной линиями (слайд 14)

, х=0, у= вокруг оси Оу

Решение:

Аналогично можно доказать, что объём тела, полученного вращением вокруг оси Оу можно вычислить по формуле 

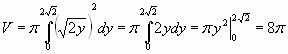
Применение определённого интеграла в физике

1. Работа. (слайд 16)

Пусть к движущейся по прямой точке приложена направленная вдоль этой прямой переменная сила F=f(x), где f(x) есть непрерывная функция от х – координаты движущейся точки. Работа силы F при передвижении точки от a до b равна

где a=x₀<x₁<…<x_n=b, ?x_j=x_j+1-x_j

в силу непрерывности функции f(x) произведение близко к истинной работе на отрезке [x_j; x_j+1], а сумма таких произведений близка к истинной работе на отрезке [a; b], и притом тем ближе, чем меньше наибольший из всех ?x_j.

№ 4.

К движущейся по прямой точке приложена направленная вдоль этой прямой сила F=2х-1, где х – координата движущейся точки. Вычислите работу силы F по перемещению точки от 0 до 3. (слайд 17)

Решение: 

2. Масса стержня переменной плотности (слайд 18)

Будем считать, что отрезок [a; b] оси Ох имеет массу с переменной линейной плотностью , где - непрерывная на отрезке [a; b] функция. Общая масса этого отрезка 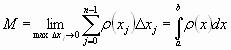, где a=x₀<x₁<…<x_n=b, ?x_j=x_j+1-x_j

№ 5. Вычислить массу стержня на отрезке от 0 до 2, если его плотность задаётся функцией (слайд 19)

Решение: