
- •5.2. Физические процессы происходящие в системе с двумя p-n переходами
- •5.2.1. Основные физические процессы в биполярных транзисторах
- •5.2.2. Биполярный транзистор в схеме с общей базой. Зонная диаграмма и токи
- •5.2.3. Модуляция ширины базы. Эффект Эрли
- •5.2.4. Дифференциальные сопротивления переходов биполярного транзистора
- •5.2.5. Коэффициент обратной связи
5.2.3. Модуляция ширины базы. Эффект Эрли
При нормальном включении биполярного транзистора на эмиттерный переход подается прямое смещение Uэп , а на коллекторный переход – обратное, Uкп.
Рассмотрим, как такое включение влияет на изменение ширины базы биполярного транзистора (рис. 5.21).
В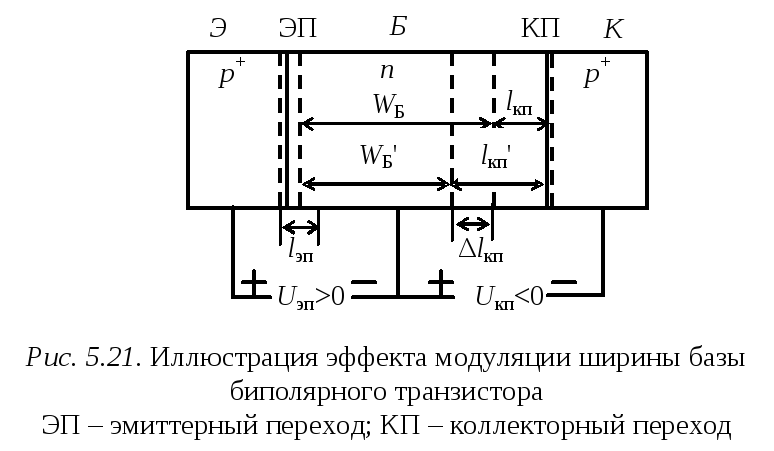 эмиттерном переходе, включенном в прямом
направлении, ширина запирающего слоя
распространяется в область базы и равна
эмиттерном переходе, включенном в прямом
направлении, ширина запирающего слоя
распространяется в область базы и равна
 ≈0,1
мкм.
≈0,1
мкм.
К коллекторному переходу приложено обратное напряжение и ширина запирающего слоя, распространяющегося в область менее легированной базы, значительно больше:
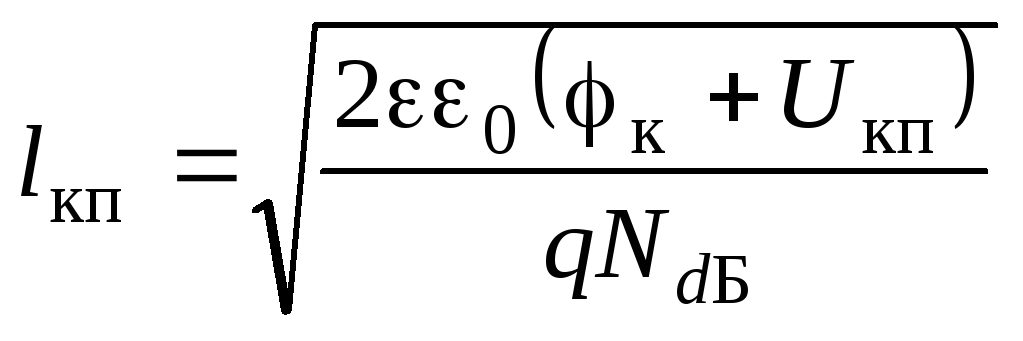 ≈1…5
мкм.
≈1…5
мкм.
Увеличение абсолютного значения обратного напряжения Uкп ведет к уменьшению ширины базы на величину WБ′= WБ - Δlкп (рис 5.21). Этот эффект называют модуляцией ширины базы.
Рассмотрим, как модуляция ширины базы влияет на коэффициент передачи . Проанализируем возможность зависимости коэффициента передачи от напряжения на коллекторе Uк. Эта зависимость может проявиться через следующие цепочки: увеличение напряжения на коллекторе Uк увеличит ширину запирающего слоя p‑n перехода lкп, а увеличение ширины запирающего слоя p‑n перехода вызовет уменьшение ("модуляцию") ширины базы.
Из-за
уменьшения ширины базы WБ
при увеличении напряжения Uк
на коллекторе отношение
![]() будет уменьшаться, гдеL
– диффузионная длина инжектированных
носителей является неизменной величиной.
Поэтому скорость рекомбинации избыточных
носителей в базе также будет уменьшаться
и большее количество неосновных
носителей заряда дойдет до коллектора.
В результате ток коллектора Iк
возрастает, а так как
будет уменьшаться, гдеL
– диффузионная длина инжектированных
носителей является неизменной величиной.
Поэтому скорость рекомбинации избыточных
носителей в базе также будет уменьшаться
и большее количество неосновных
носителей заряда дойдет до коллектора.
В результате ток коллектора Iк
возрастает, а так как
![]() ,
то увеличивается коэффициент передачи
тока эмиттера.
,
то увеличивается коэффициент передачи
тока эмиттера.
Зависимость
от отношения
![]() ширины
базыW
к диффузионной длине носителей заряда
L
очевидна из анализа выражения (4.61) для
коэффициента передачи :
ширины
базыW
к диффузионной длине носителей заряда
L
очевидна из анализа выражения (4.61) для
коэффициента передачи :
![]() ,
,
откуда
следует, что при уменьшение отношения
![]() коэффициент передачи тока эмиттера
возрастает, а при увеличении
коэффициент передачи тока эмиттера
возрастает, а при увеличении![]() значение
уменьшается.
значение
уменьшается.
Изменение коэффициента передачи биполярного транзистора вследствие модуляции ширины базы при изменении коллекторного напряжения Uк получило название “эффект Эрли”.
Как следствие, на зависимости Iк= f(Uк)|Iэ=const при увеличении напряжения Uк на коллекторном переходе несколько возрастает и ток коллектора Iк. Это свидетельствует о том, что значение дифференциального сопротивления rк обратно-смещенного коллекторного перехода имеет хотя и высокое, но конечное значение.
5.2.4. Дифференциальные сопротивления переходов биполярного транзистора
Дифференциальное сопротивление коллекторного перехода rк определяется как
![]() .
(5.26)
.
(5.26)
 В
активном режиме при Uк << 0
зависимость тока коллектора Iк
от параметров биполярного транзистора
выглядит следующим образом: Iк = Iэ + Iк0.
Из приведенного соотношения следует,
что в явном виде ток коллектора Iк
от напряжения на коллекторе Uк
не зависит. Поэтому в первом приближении
сопротивление коллекторного перехода
rк
при Uк << 0
стремится к бесконечности.
В
активном режиме при Uк << 0
зависимость тока коллектора Iк
от параметров биполярного транзистора
выглядит следующим образом: Iк = Iэ + Iк0.
Из приведенного соотношения следует,
что в явном виде ток коллектора Iк
от напряжения на коллекторе Uк
не зависит. Поэтому в первом приближении
сопротивление коллекторного перехода
rк
при Uк << 0
стремится к бесконечности.
С учетом изложенного выражение (5.26) для расчета дифференциального сопротивления коллекторного перехода rк представим в виде:
![]() .
(5.27)
.
(5.27)
При
изменении напряжения на коллекторе Uк
меняется ширина обедненной области
![]() ,
а, следовательно, и ширина базы биполярного
транзистораW.
Этот эффект обуславливает конечное
значение дифференциального сопротивления
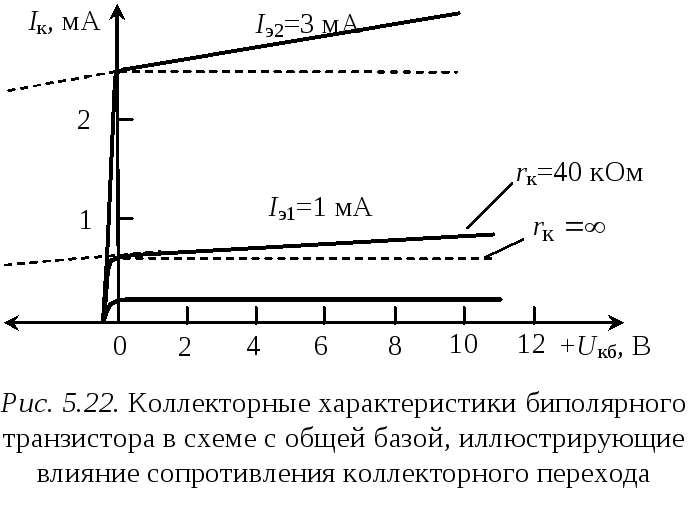
коллекторного перехода (рис. 5.22).
Соотношение (5.27) можно представить в
виде:
,
а, следовательно, и ширина базы биполярного
транзистораW.
Этот эффект обуславливает конечное
значение дифференциального сопротивления
коллекторного перехода (рис. 5.22).
Соотношение (5.27) можно представить в
виде:
![]() .
(5.28)
.
(5.28)
Подставляя
значение
![]() в соотношение (5.28) с учетом сказанного
получаем выражение для дифференциального
сопротивления коллекторного перехода:
в соотношение (5.28) с учетом сказанного
получаем выражение для дифференциального
сопротивления коллекторного перехода:
![]() .
(5.29)
.
(5.29)
Пример. Рассчитать численное значение сопротивления коллекторного перехода rк при следующих параметрах биполярного транзистора на основе кремния (Si): ND = 1015 см-3; L = 0,1 мм; W = 30 мкм, Uк = 5В, Iэ = 1 мА, Si = 11,8.
Подставляя параметры в выражение (5.29), получаем rк 5,2 МОм.
На рисунке 5.22 приведены выходные характеристики Iк= f(Uк)|Iэ=const биполярного транзистора в схеме с ОБ, иллюстрирующие влияние конечного сопротивления коллекторного перехода, обусловленным эффектом Эрли. Заметим, что пересечения продолжений пологих частей коллекторных характеристик с осью напряжений сходятся в одной точке. Напряжение, соответствующее этой точке называется напряжением Эрли и приводится в качестве справочных данных на транзистор.
С учетом дифференциального сопротивления коллекторного перехода выражение (5.21) для коллекторного тока в схеме с ОБ приобретает вид
![]() ,
(5.30)
,
(5.30)
где Uкб – обратное напряжение коллектор-база.
Для расчета дифференциального сопротивленияе эмиттерного перехода используется выражение (4.15) для прямосмещенного p-n перехода:
![]() ,
,
где Iэ – ток через эмиттерный переход.
