Гальваномагнитные

Эффект Холла

Эффект, открытый американским физиком Эдвином Гербертом Холлом в 1879 году, заключается в явлении возникновения попереч- ной разности потенциалов в полупроводнике, по которому протекает электрический ток и суще- ствует магнитное поле Н, перпендикулярное на-

правлению тока.

Физическая природа эффекта Холла заключается в том, что на движущийся носитель тока в магнитном поле с индукцией В действует сила Лоренца

где v –скорость носителя; q – его заряд.

2

где Uх (0,6…1)·10-4 В - разность потенциалов между поперечными гранями

пластинки, называемая эдс Холла; а – ширина пластинки (рис. 1).

Поле Ех действует на электроны с силой F=-qEх, направленной против силы Лоренца Fл. При выполнении условия Fл=F поперечное электрическое

поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов на боковых гранях пластины прекращается. Тогда из равенства

где j – плотность тока, А/м2, n – концентрация электронов, м-3.

4

Тогда выражение для поля Ех приобретает вид.

5

С учетом разброса средней скорости дрейфа электронов в полупроводнике значение коэффициента Холла определяется из выражения

где А=1,18 для полупроводников с преимущественным рассеянием носителей заряда на тепловых колебаниях кристаллической решетки; А=1,93 при рассеянии на ионизированных примесях.

Для дырочных полупроводников коэффициент Холла рассчитывается по формуле

где q и p –заряд и концентрация дырок, соответственно.

6

При смешенной электронно-дырочной проводимости величина коэффициента Холла рассчитывается по формуле

соответственно.

Из формулы (6.20) следует, что в собственных полупроводниках при выполнении условия ni=pi значение

коэффициента Холла равно

7

Преобразователи Холла

Это гальваномагнитные полупроводниковые

приборы, основанные на использовании эффекта Холла.

ЭДС преобразователя Холла конечной длины рассчитывается по формуле

где J – ток через преобразователь, А; δ – толщина преобразователя, м; l – длина преобразователя; а –

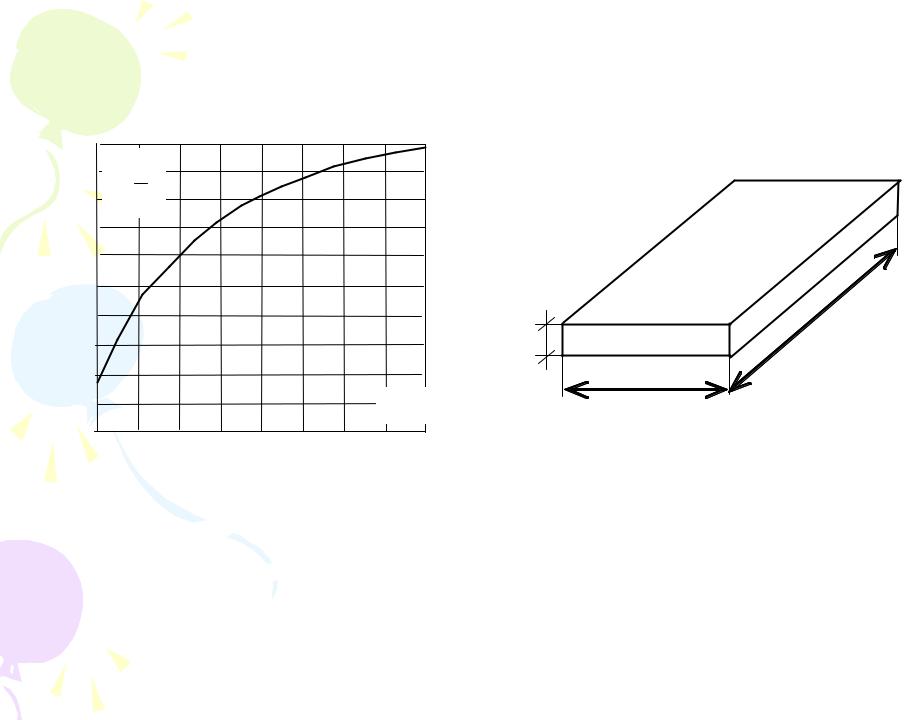
функция, график которой приведен на рис. 2.

8

Рис. 2. Зависимость поправочной функции f(l/a)от размеров

преобразователя

9

Материалом для преобразователя Холла служит монокристаллическая пластинка из Ge или InSb. Эти материалы характеризуются высокой подвижностью электронов. Также используются тонкие пленки с толщиной δ=0,01…0,1 мкм, нанесенные на диэлектрическую подложку методом испарения в вакууме. В этом случае материалами служат HgSe, HgTe, сплавы HgSe-HgTe, в которых подвижность электронов достигает значения 1 м2/ (В·с).

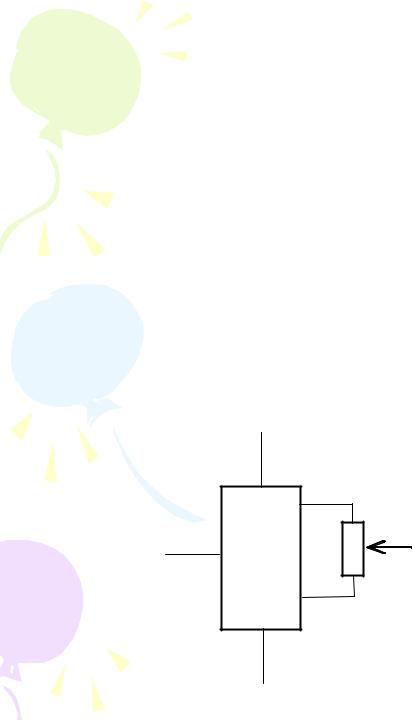
Конструкция преобразователя Холла показана на рис. 3. Для устранения неэквипотенциальности выходных электродов 2-2 в схеме подключения преобразователя предусмотрен переменный резистор Rк. Предельная частота работы преобразователей Холла достигает 10…100 МГц.