
- •Влажный воздух Основные определения и характеристики
- •Конденсационный гигрометр.
- •И тогда,
- •Плотность влажного воздуха:
- •Молекулярная масса влажного воздуха:
- •Влагосодержание влажного воздуха
- •Тогда ,
- •Газовая постоянная r влажного воздуха:
- •Объем влажного воздуха, приходящегося на 1кг сухого, находят из условия
- •Энтальпия I влажного воздуха, отнесенная к 1 кг сухого воздуха:
Плотность влажного воздуха:
Плотность влажного воздуха по законам газовых смесей (см. метод. пособие «Газовые смеси и смешение газов»):
![]()
![]()
Где
![]() -
парциальное давление сухого воздуха(
-
парциальное давление сухого воздуха(![]() ),
),
![]() ,
,
![]() ,В
– барометрическое давление,
,В
– барометрическое давление,
![]() -
удельный объем сухого насыщенного пара
(по таблицам),
-
удельный объем сухого насыщенного пара
(по таблицам),
φ – относительная влажность (по данным психрометра)
Окончательно
![]()
Молекулярная масса влажного воздуха:
Известно для
смеси
 ,
где
,
где![]() (
(![]() -объемная
доля).
-объемная
доля).
Для нашего случая Рсм = В.
![]() - объемная доля
сухого воздуха
- объемная доля
сухого воздуха
![]() - объемная доля
водяного пара
- объемная доля
водяного пара
![]()
Тогда
![]()
Окончательно
![]()
Рн – давление насыщения пара при температуре воздуха (температуре сухого термометра).
Молекулярная масса влажного воздуха меньше, чем сухого воздуха, т.е. влажный воздух легче сухого.
Влагосодержание влажного воздуха
В процессе сушки влажность воздуха непрерывно увеличивается, а количество сухого воздуха в паровоздушной смеси остается постоянным, поэтому о процессе сушки судят по тому, как изменяется количество водяного пара на 1 кг сухого воздуха. Такие показатели паровоздушной смеси как теплоемкость, влагосодержание, энтальпия и др. относят к 1 кг сухого воздуха, находящегося во влажном воздухе.
Например, если на 1 кг сухого воздуха приходится dкг водяных паров, то общая масса смеси на 1 кг сухого воздуха, находящегося во влажном воздухе, составляет (1+d) кг.
Влагосодержание влажного воздуха – это отношение массы пара к массе сухого воздуха, содержащихся в паровоздушной смеси, т.е.
![]() , [кг/кг]
, [кг/кг]
где Мп, Мв – масса пара и масса сухого воздуха во влажном воздухе.
![]() - массовые доли
пара и сухого воздуха во влажном воздухе.
- массовые доли
пара и сухого воздуха во влажном воздухе.
Известно, что
![]() ,
т.е.
,
т.е.![]() ;
;![]()
Тогда ,
но
![]() и
и![]()
Окончательно
![]() (1)
(1)
Максимально возможное содержание влаги в воздухе будет при φ=1:
![]() (2)
(2)
Т.к. давление
насыщения Рн растет с повышением
температуры, то
![]() зависит от температуры воздуха тем
больше, чем она выше.
зависит от температуры воздуха тем
больше, чем она выше.
Обозначение:
![]() , (3)
, (3)
где Ψ – степень насыщения влажного воздуха. Из формулы (3) следует, что при φ близком к 1, значения Ψ и φ примерно одинаковы.
Из уравнения (1)
выразим Рп:
![]()
Из уравнения (2)
выразим Рн:
![]()
Откуда
![]()
![]()
Газовая постоянная r влажного воздуха:
![]()
 ,
,
Объем влажного воздуха, приходящегося на 1кг сухого, находят из условия
BVвл.в= (1кг +d)RT=>![]()
Удельный объем влажного воздуха [м3/кг] найдем, если объем влажного воздуха, приходящегося на 1 кг сухого (Vвл.в), разделим на его массу (1+d) кг:
![]()
Удельную массовую теплоемкость паровоздушной смеси, отнесенную к 1 кг сухого воздуха,определяют по формуле:
![]() - это для 1 кг
смеси, где содержится
- это для 1 кг
смеси, где содержится
![]() кг сухого воздуха. Таким образом если
относить все к 1 кг сухого воздуха, то
нужно разделить Ссм наgв:
кг сухого воздуха. Таким образом если
относить все к 1 кг сухого воздуха, то
нужно разделить Ссм наgв:
![]()
![]()
Приближенно:
![]() - для Р = constиt< 100C.
- для Р = constиt< 100C.
![]() - для Р =Ратм и
невысоких степенях перегрева.
- для Р =Ратм и
невысоких степенях перегрева.
Энтальпия I влажного воздуха, отнесенная к 1 кг сухого воздуха:
![]()
Для обеспечения одинаковости точек начала отсчета энтальпий полагают, что как и у воды энтальпия сухого воздуха при 0 С равна нулю.
Таким образом
![]() .
.
Энтальпия перегретого водяного пара, содержащегося во влажном воздухе:
![]() ,
,
где
![]() ;
;![]()
![]()
![]() - для
- для
![]() от 0 до 100 С.
от 0 до 100 С.
Тогда после подстановки этих значений:
![]()
и
![]()
I – d – диаграмма для влажного воздуха и её построения.
J-dдиаграмма была предложена российским ученым Л.К. Рамзиным в 1918г.J-dдиаграмма удобна для определения параметров влажного воздуха и решения практических задач, связанных с сушкой материалов.
Построена для В = 98 кПа(это среднегодовое барометрическое давление в центральных районах РФ). Обычные колебания В мало сказываются наJ-dдиаграмме.
Принцип построения:
В области ненасыщенноговоздуха (где пар находится в перегретом состоянии):
iв=Св·t=1,0048t
iп=
2500 + 1,96t
, , но ,
- сухой воздух и тогда из уравнения

J= 1,0048t+ (2500+1,96t)d,
следует, что изотермывI-dдиаграмме – это прямые линии с угловым коэффициентом.
![]()
,
из этого уравнения следует, что с ростом температуры наклон изотерм увеличивается.
И зотермы
удобно строить, задаваясьd=0
иd=dн
зотермы
удобно строить, задаваясьd=0
иd=dн![]() .
Т.к. влагосодержаниюdн
соответствует относительная влажность
воздуха φ=100% то, соединив точкиdнвсехизотерм получим кривую насыщения
φ=100% для В=98 кПа.
.
Т.к. влагосодержаниюdн
соответствует относительная влажность
воздуха φ=100% то, соединив точкиdнвсехизотерм получим кривую насыщения
φ=100% для В=98 кПа.
Но при этом получается, что наиболее важная областьненасыщенного пара на диаграмме, получаетсяочень узкой и вытянутой,что очень не удобно для практики.
Поэтому для удобствапрямоугольную систему заменяюткосоугольной, с углом между осями абсцисс и ординат 1350.

При этом изотерма t=00С в несыщенной области располагаетсяпочтигоризонтально. ЛинииJ=const– уже не горизонтальные, а наклонные прямые под углом 1350. Для удобства влагосодержаниеdсносят (проецируют) нагоризонтальнуюпрямую, проходящую через начало координат (в дальнейшем остаетсятолько эта прямая – как осьd, а низотбрасывается!).
Д
 алее
на диаграмме проводитсясправа
дополнительнаяось Рп – парциального
давления водяного пара и по уравнению
алее
на диаграмме проводитсясправа
дополнительнаяось Рп – парциального
давления водяного пара и по уравнению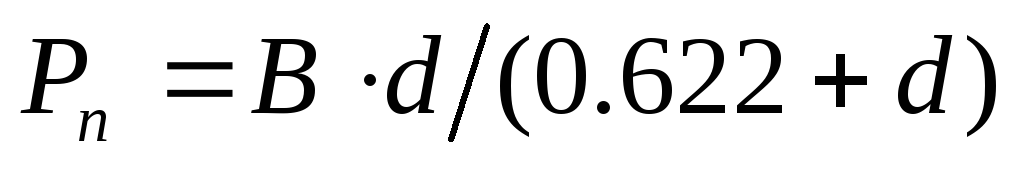 строится кривая Рп=Рп(d),
выходящая из начала координат. Эта
кривая строится в нижней части диаграммы.
строится кривая Рп=Рп(d),
выходящая из начала координат. Эта
кривая строится в нижней части диаграммы.
Далее на J-dдиаграмме наносятся линии φ=const. Для этого длязаданногозначения φ определяют по таблицам водяного пара для ряда значений температурt1,t2,t3, ….:

Затем на кривой Рп=Рп(d) находят соответствующие Рп, из этих точек проводятся прямые параллельные осиIдо пересечения с соответствующими изотермамиt1,t2,t3. Точки пересечения соединяют и получают кривую линиюφ=const.
Кривая φ=100% разделяет I-dдиаграмму наверхнююобластьвлажного ненасыщенного воздухаинижнююобластьпересыщенного воздуха,в котором влага может находиться в капельном состоянии (область тумана). Линия φ=100% -максимальноевозможное насыщение влагой воздуха при данной температуре. На практике используетсяI-dдиаграмма ВТИ.I-dдиаграмма ВТИ построена по точным формулам, т.е. водяной пар в воздухене считаетсяидеальным газом.
На диаграмме ВТИ при t>1000С (точнее 99,40С – этоtнасдля В=98кПа) линии φ=constидут почти вертикально вверх.
По приближенным формулам
![]() ,
и
,
и
![]()
![]()
,
но т.к. при t=99,40С Рн=В=98кПа, то приd=constи φ=const, т.е. линии φ=constидут поd=const).
В современных
изданиях I–d- диаграмм приведены также линии
постоянных истинныхтемператур мокрого
термометра![]() .
Коротко остановимся на ней.
.
Коротко остановимся на ней.
При испарении
влаги в процессе сушки I=const, т.к. теплотаотбираемаяот воздуха для просушивания материалавозвращаетсяк нему вместе с
испаряемой влагой, т.е. в уравнении![]() уменьшение первого слагаемого
уменьшение первого слагаемого![]() компенсируется увеличением второго
слагаемого
компенсируется увеличением второго
слагаемого![]() .
Этот процесс приI=constусловноназывается процессомадиабатного испарения. (При этом
полагается, что начальная температура
воды = 0 С).
.
Этот процесс приI=constусловноназывается процессомадиабатного испарения. (При этом
полагается, что начальная температура
воды = 0 С).
Температура
воздуха при сушке уменьшается и пределом
её понижения является температура
адиабатного насыщения воздуха(«адиабатная температура мокрого
термометра») -![]() .
Эта температура
.
Эта температура![]() находится на диаграмме как температура
точки пересечения линииI=constс кривой насыщения
φ=100%.
находится на диаграмме как температура
точки пересечения линииI=constс кривой насыщения
φ=100%.
Если начальная
температура воды > 0 С, то с водой будет
вноситься в воздух дополнительное
количество теплотыи адиабатность
процесса испарения нарушается. В этом
случае![]() и линия
и линия![]() идет более полого, чемI=constидействительную
температуру мокрого термометранаходят как температуру точки на
пересечении линии
идет более полого, чемI=constидействительную
температуру мокрого термометранаходят как температуру точки на
пересечении линии![]() с кривой φ=100%.
с кривой φ=100%.
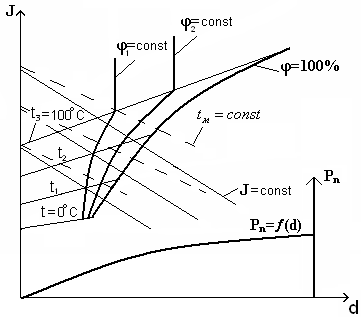
На диаграмме штриховой линией нанесены линии постоянной температуры мокрого термометра– это температура, приобретаемая водой, если поверхность ее обдувается потоком влажногоненасыщенноговоздуха. Если поверхность обдувается потокомнасыщенноговоздуха, то температура водысовпадаетс температурой воздуха. Поэтому наI-dдиаграмме изотермы сухого и мокрого термометров пересекаютсяна линии насыщенного воздуха, т.е. φ=100%.
В процессе нагреваниявлажного воздуха (например, в калорифере сушилки) влагосодержаниеdне изменяется, а относительная влажность уменьшается, поэтому нагрев (и охлаждение) изображаются прямой линиейd=const.
Температура, при которой в процессе охлаждения достигается φ=100%, называется точкой росы. На данном рисунке это температура изотермыtp.

АМВ – процесс охлаждения воздуха; точка А- ненасыщенный воздух; точка М – насыщенный влажный воздух; точка В – пересыщенный воздух.
При дальнейшем охлаждении ниже точки росы (точка В) смесь (туман) будет содержать воду в виде:
а) сухого насыщенного пара в количестве dN;
б) в виде жидкости в количестве (dB-dN).
Если в сушилке нет тепловых потерь то, пренебрегая начальной энтальпией испаряемой жидкости, процесс сушки идет по изоэнтальпе (например, линия Е-Д).
Энтальпия воздуха при испарении влаги остается постоянной, т.к. теплота, отбирается от воздуха для подсушивания материалов, возвращается обратно к нему вместе с испаренной влагой, т.е. в уравнении
![]() ,
,
уменьшение первого слагаемого будет компенсироваться увеличением второго слагаемого. Если есть тепловые потери, то процесс условно изображается линией Е-F. При этом энтальпия влажного воздуха на выходе из сушилки уменьшится на размер тепловых потерь:
![]() ,
,
если бы процесс сушки совпадал с изоэнтальпой, то состояние влажного воздуха можно было бы в I-dдиаграмме определить по показаниям сухого (tc) и мокрого (tм) термометров (точка пересечения этих двух изотерм, одна из которыхI=tм=const).
Но действительный процесс отличается от адиабатного, поэтому для определения состояния влажного воздуха по показаниям сухого и мокрого термометров пользуются психрометрической формулой:
![]() ,
,
где:
Рп – парциальное давление водяного пара;
Рнм – давление насыщения водяного пара при температуре мокрого термометра (определяется по таблицам);
В – барометрическое давление;
А – психрометрический коэффициент (при скорости обтекания воздухом
2м/с А≈67∙10-5).
далее:
![]() и
и
![]() ,
где:
,
где:
Рн – давление насыщения для tc.
Для построения изотермы мокрого термометра tмнужно:
по температуре мокрого термометра tми таблицам водяного насыщенного пара находят Рнм;
задаются рядом значений tсiи по психрометрической формуле вычисляют Рпi;
для каждой tciопределяют φi=Рпi /Рнi;
точка пересечения изотермы tсi и φiдает точку изотермы мокрого термометра.
