
Глава первая
ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
§ 1.1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Для описания физических полей принято использовать их математические модели — скалярные и векторные поля. В произвольной системе координат скалярное поле ϕ приобретает вид некоторой функции ϕ принимающей численные значения — действительные или комплексные. Векторное поле А задается тремя проекциями на единичные векторы (орты) выбранной системы координат:
A = Ax1 ( x1 , x2 , x3 )1 x1 + Ax 2 ( x1 , x2 , x3 )1 x 2 + Ax 3 ( x1 , x2 , x3 )1 x 3 .
Для характеристики величины и направления скорости изменения скалярного поля в пространстве вводят градиент этого поля
grad ϕ = |
1 |
|
∂ϕ |
1 x1 + |
1 |
|
∂ϕ |
1 x 2 + |
1 |
|
∂ϕ |
1 x 3 , |
(1.1) |
|
|
|
|
|
|
||||||||
|
h1 ∂x1 |
h2 ∂x2 |
h3 ∂x3 |
|
|||||||||
где h1, h2, h3 – коэффициенты Лямэ по координатам x1, x2, x3 являющиеся коэффициентами пропорциональности между дифференциалами обобщенных координат и бесконечно малыми ребрами элементарного параллелепипеда в выбранной точке пространства.
Приведем значения коэффициентов Лямэ для наиболее употребительных координатных систем:
декартова система координат (х, у, z)
hx = hy = hz = 1;
цилиндрическая система координат (r,ϕ, z) hr=1 , hϕ = r , hz = 1 ;
сферическая система координат (r, ϑ , ϕ) hr =1 , hϑ = r , hϕ = r sinϑ .
Конкретно градиент вычисляют следующим образом: в декартовой системе координат
grad ≡ |
∂ |
1 x + |
∂ |
1 y + |
∂ |
1 z ; |
|
∂x |
∂y |
∂z |
|||||
|
|
|
|
в цилиндрической системе координат
grad ≡ |
∂ |
1r |
+ |
1 |
∂ |
1φ + |
∂ |
1 z ; |
|
∂r |
r |
∂φ |
∂z |
||||||
|
|
|
|
|
в сферической системе координат
grad ≡ |
∂ |
1r + |
1 ∂ |
1ϑ + |
1 |
|
∂ |
1ϕ . |
|
|
|
|
|
|
|
||||
∂r |
r ∂ϑ |
rsin ϑ |
|
∂ϕ |
|||||
|
|
|
|
|
|||||
Описание дифференциальных свойств векторного поля несколько сложнее. Векторное поле А принято характеризовать скалярным полем – дивергенцией divА и векторным полем – ротором rоtА. Значение дивергенции равно плотности источников рассматриваемого поля в заданной точке пространства. Трактовка ротора векторного поля сложнее, можно считать, что оно в известном смысле характеризует степень отличия исследуемого поля от однородного.
Дивергенцию векторного поля А вычисляют путем дифференцирования его проекций по определенным правилам:
в декартовой системе координат
div A = |
∂Ax |
+ |
∂Ay |
+ |
∂Az |
; |
(1.2) |
|
∂x |
∂y |
|
∂z |
|||||
в цилиндрической системе координат |
|
|
|
|
||||
|
|
|
|
div A = |
1 |
|
∂ |
(rAr ) + |
1 |
|
∂Aϕ |
+ |
|
∂A |
z |
; |
|
|
(1.3) |
|||||||
|
|
|
|
r |
∂r |
r |
|
∂ϕ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|||||||||
в сферической системе координат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
div A = |
1 |
|
∂ |
(r |
2 |
Ar |
) + |
|
|
1 |
|
∂ |
|
|
(sin ϑAϑ |
) + |
|
1 |
|
∂Aϕ |
. (1.4) |
|||||
r |
2 |
|
∂r |
|
|
rsin ϑ |
|
∂ϑ |
|
|
rsin ϑ |
|
∂ϕ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В произвольной ортогональной криволинейной системе координат
|
1 |
|
|
|
∂ |
|
|
∂ |
|
|
∂ |
|
|
|
|
|
div A = |
|
|
|
|
|
|
|
( h2 h3 Ax1 ) + |
|
|
( h1h3 Ax2 ) + |
|
|
( h1h2 Ax3 |
) |
. (1.5) |
h h |
|
h |
|
∂x |
|
∂x |
|
∂x |
|
|||||||
|
1 |
2 |
|
3 |
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
Проекции ротора векторного поля имеют вид:
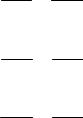
в декартовой системе координат
(rot A) x = ∂∂Ayz − ∂∂Azy ,
(rot A) y = ∂∂Azx − ∂∂Axz ,
(rot A) z = ∂∂Axy − ∂∂Ayx ;
в цилиндрической системе координат
(rot A) r = |
1 |
|
∂A |
z |
− |
|
∂Aϕ |
|
|
, |
|
||||||||
r |
∂ϕ |
|
|
|
|
∂z |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(rot A) ϕ |
= |
|
∂Ar |
|
− |
|
∂Az |
|
, |
|
|
|
|||||||
|
∂z |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
|||||
(rot A) z = |
1 |
∂(rAϕ ) |
− |
∂A |
r |
|
|
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
r |
|
|
∂r |
|
|
∂ϕ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в сферической системе координат
|
|
|
|
1 |
|
|
∂(sin ϑ A |
) |
|
|
|
∂Aϑ |
|
|
, |
|||||||||||
(rot A ) r |
= |
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
− |
|
|
|
||||||
rsin ϑ |
|
|
∂ϑ |
|
|
|
|
|
|
|
∂ϕ |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
( rot A )ϑ |
= |
1 |
|
|
1 |
|
|
∂A |
r |
|
− |
∂(rA ϕ |
) |
, |
||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
∂ϕ |
|
|
|
∂r |
|
|
||||||||||||||
|
|
|
sin ϑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(rot A )ϕ |
= |
|
1 |
∂(rA |
ϑ |
) |
− |
|
|
∂A |
r |
|
|
|
|
|
|
|||||||||
|
r |
|
∂r |
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||
|
|
|
|
∂ϑ |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(1.6)
(1.7)
(1.8)
Ротор векторного поля А в произвольной системе координат выражают через проекции исходного поля и коэффициенты Лямэ:
|
1 |
x1 |
|
|
|
∂(h |
3 |
A |
) |
|
∂(h |
2 |
A |
x2 |
) |
|
|
1 |
x2 |
|
|
|
∂(h A |
) |
|
∂(h |
3 |
A |
) |
|
||||||||
rot A = |
|
|
|
|
|
|
|
x3 |
− |
|
|
|
|
|
|
|
+ |
|
|
|
1 |
|
x1 |
− |
|
|
x3 |
|
+ |
|||||||||
h |
h |
|
|
∂x |
|
|
|
|
∂x |
|
|
|
h h |
|
|
∂x |
|
|
∂x |
|
||||||||||||||||||
|
3 |
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
∂(h A |
) |
|
|
∂(h A |
) |
|
|
|
|
|
|
|
|
(1.9) |
||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
x3 |
|
|
|
|
2 |
x2 |
|
− |
|
|
1 |
x1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x1 |
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
h1h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Дифференциальные операции со скалярными и векторными полями |
||||||||||||||||||||||||||||||||||||||
удобно записывать с помощью оператора Гамильтона . По определению |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
gradU |
|
= U , |
|
|
div A = A , |
|
rot A = [ A]. |
|
|
|
|
|
(1.10) |
|||||||||||||||||||||
В декартовой системе координат оператор Гамильтона есть символический вектор
≡ |
∂ |
1 x + |
∂ |
1 y + |
∂ |
1 z . |
(1.11) |
|
∂x |
∂y |
∂z |
||||||
|
|
|
|
|
Из дифференциальных векторных операций второго порядка широкое применение в электродинамике находит оператор 2, закон действия которого на векторное поле А описывается соотношением
|
|
|
|
|
|
|
|
|
|
2 A = grad div A − rot |
rot A . |
|
|
(1.12) |
|||||||||||||||||
Дифференциальная операция второго порядка, действующая на |
|||||||||||||||||||||||||||||||
скалярное поле, задается оператором Лапласа |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= ∆ ≡ div |
|
grad . |
|
|
|
|
|
||||||||||
Оператор Лапласа в различных координатных системах записывается |
|||||||||||||||||||||||||||||||
следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
в декартовой системе координат |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 U = |
∂ 2 U |
+ |
|
∂ 2 U + |
∂ 2 U |
; |
|
|
(1.13) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x 2 |
|
|
|
∂y 2 |
∂z 2 |
|
|
|
|
||||||
в цилиндрической системе координат |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
1 ∂ |
|
|
∂U |
|
|
|
1 ∂ |
2U |
|
∂ 2U |
; |
|
(1.14) |
||||||
|
|
|
|
|
|
|
|
U |
= |
|
|
|
r |
|
|
+ |
|
|
|
|
|
+ |
|
|
|||||||
|
|
|
|
|
|
r ∂r |
∂r |
r 2 ∂ϕ |
2 |
∂z 2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
в сферической системе координат |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
1 |
|
∂ |
|
|
2 |
∂U |
|
|
1 |
|
|
|
∂ |
|
|
∂U |
|
1 |
∂ 2U |
.(1.15) |
|||||||
|
|
U |
= |
|
|
|
r |
|
|
+ |
|
|
|
|
|
|
|
|
sin |
ϑ |
|
|
+ |
|
|
||||||
|
r 2 |
|
|
∂r |
r 2 sin ϑ ∂ϑ |
|
|
∂ϑ |
r 2 sin 2ϑ ∂ϕ 2 |
||||||||||||||||||||||
|
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Для графического изображения векторных полей принято строить картину их силовых линий. В каждой точке силовой линии вектор поля касателен к ней. Там, где интенсивность поля больше, силовые линии проводят чаще, и наоборот.
§ 1.2. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
1.1. В декартовой системе координат проекции векторного поля А постоянны в каждой точке пространства: Ax = A0 , Ay = B0 , Az = 0 .
Построить картину силовых линий векторного поля.
Решение. Поскольку одна из декартовых составляющих векторного поля отсутствует, силовые линии должны представлять собой семейство плоских кривых, лежащих в плоскостях, параллельных плоскости ху. Вектор поля в каждой точке касателен к силовой линии, откуда вытекает дифференциальное уравнение силовых линий
dx / A0 = dy / B0 , |
(1.16) |
являющееся следствием подобия двух прямоугольных треугольников с катетами dх, dу и А0, В0 соответственно. Общий интеграл уравнения (1.16) имеет вид
у= (В0/А0)х+ С,
где С – произвольная постоянная.
Таким образом, силовые линии поля представляют собой однопараметрическое семейство прямых с угловым коэффициентом наклона
коси х, равным В0 /А0 (рис. 1.1).
1.2.Векторное поле А, удовлетворяющее во всех точках рассматриваемой области условию divА = 0, называется соленоидальным (полем без источников). При выполнении условия rotА=0 поле А является потенциальным векторным полем. Если такое поле характеризует силу, действующую на материальную точку, то работа внешних сил при обходе замкнутого контура будет равна нулю.
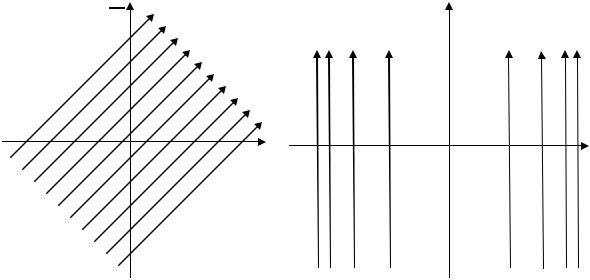
В декартовой системе координат векторное поле А имеет
единственную составляющую Аy =15х2.
Проверить, является ли поле: а) соленоидальным; б) потенциальным. Решение. Картина силовых линий поля А в плоскости ху изображена на
рис. 1.2. Вычисляя дивергенцию этого поля по формуле (1.2), получим, что divА=∂Аy/∂y=0. Следовательно, исследуемое поле соленоидально. Однако в соответствии c (1.6) rotА=30х1z, поэтому поле не является потенциальным.
y
y
A
A
0 |
0 |
x |
|
x
Рис. 1.1 |
Рис. 1.2 |
1.3. Вычислить дивергенцию векторного произведения полей А и В. Решение. Здесь удобно воспользоваться оператором Гамильтона,
записав
div [AB ]= [AB ].
Оператор Гамильтона является дифференциальным оператором, поэтому к приведенному векторному произведению можно применит обычные правила дифференцирования произведения:
[AB ]= A [AB ]+ B [AB ].
Нижние индексы у оператора указывают поле, на которое он воздействует. Поле, на которое оператор не воздействует, должно быть вынесено за знак оператора подобно константе. В результате получаем
div [AB ]= B[ A A ]+ A[ B B ]= B rot A − A rot B .
§ 1.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.4. Скалярное поле ϕ задано в декартовой системе координат выражением
ϕ = 3x 2 y cos z + 2 z 2 .
Вычислить векторное поле grad ϕ.
Ответ: grad ϕ = 6 xycosz 1 x + 3x 2 cosz 1 y + (4 z − 3x 2 ysinz )1 z .
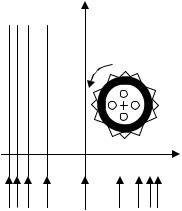
1.5. В декартовой системе координат векторное поле А имеет единственную составляющую Аz=3у2.
Построить качественно пространственную картину распределения силовых линий поля. Вычислить векторное поле rotА.
Ответ: rot А=6у1х.
1.6. Пусть поле А предыдущей задачи характеризует векторы скоростей потока жидкости. В любую точку пространства может быть помещена миниатюрная «турбина» с прямыми лопатками (рис. 1.3); ориентация ее оси произвольна.
Почему не будет вращаться «турбина», помещенная в поток жидкости со скоростями, одинаковыми в каждой точке? Почему угловая скорость вращения равна нулю при у=0 и изменяет направление при переходе из области у<0 в область у>0? Установить связь этих результатов с математическим понятием ротора векторного поля как циркуляции по бесконечно малому контуру.
Z |
|
|
|
|
|
|
|
|
|
|
|
|
1.7. В сферической системе координат |
|
|
|
|
|
|
|
|
|
|
|
|
|
задано векторное поле А=r1r. |
|
|
|
|
|
|
Определить скалярное поле divA. |
|
|
|
|
|
|
Качественно построить картину силовых |
|
|
|
|
|
|
|
0 |
|
|
|
|
Y |
линий векторного поля. |
|
|
|
|
Ответ: div А=3. |
||
|
|
|
|
|
A |
|
Рис. 1.3 |
|
|
|
|
1.8. В сферической системе координат |
|
векторное поле А имеет единственную r-ю составляющую, причем Аr= f(r). Какова должна быть функция f(r), чтобы дивергенция поля А
обращалась тождественно в нуль? Построить картину силовых линий поля. Ответ: f(r)=a/r2, где а – константа.
1.9.В декартовой системе координат скалярное поле ϕ имеет вид
ϕ= ехр (–j kr),

где - j =  −1 мнимая единица;
−1 мнимая единица;
k = k x 1x + k y 1y + k z 1z — постоянный вектор; r = x1x + y1y + z1z — радиус-вектор.
Найти выражения для gradϕ и ∆ϕ.
Ответ: grad ϕ = -jkexp(-j kr ) , ∆ϕ = −k 2 exp(-j kr ) ,
где k 2 = k x2 + k y2 + k z2 .
1.10. Определить дивергенцию и ротор векторного поля, имеющего в декартовой системе координат единственную составляющую
Ax = 20 sin( x / π ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: div A = |
20 |
|
x |
|
||
π |
cos |
|
|
, rot A = 0 . |
||
|
||||||
|
|
|
π |
|
||
1.11. Определить дивергенцию и ротор векторного поля А, характеризуемого следующими составляющими в цилиндрической системе координат: Ar = 10 / r 2 , Aϕ = 0 , Az = 0 .
Ответ: div A = −10 / r 3 , rot A = 0 .
1.12. Определить дивергенцию и ротор векторного поля А, имеющего в сферической системе координат единственную составляющую
Aϑ = 8r exp( −10 r ).
Ответ: div A = 0 , rot A =16(1−5r)exp(−10r)1ϕ .
1.13. В декартовой системе координат некоторое скалярное поле задано трехмерным интегралом Фурье
ϕ = |
1 |
|
|
∫ +∞∫∫Ф(k1 , k 2 , k3 ) exp [j(k1 x + k 2 y + k 3 z )]dk 1 dk 2 dk 3 . |
|||||
(2π ) |
3 |
||||||||
|
|
|
−∞ |
|
|
|
|
||
Вычислить ∆ϕ. |
|
|
|
||||||
Ответ: |
∆ϕ |
= |
|
1 |
|
∫+∞∫∫F (k1 , k 2 , k3 ) exp [j(k1 x + k 2 y + k3 z )]dk1dk 2 dk 3 , |
|||
(2π ) |
3 |
||||||||
|
|
|
|
|
|
|
−∞ |
||
где F =−(k12 +k22 +k32 )Ф.
1.14. Изобразить графически картину силовых линий векторных полей,

заданных в декартовой системе координат своими проекциями:
Ax = y +10, Ay = 0 , Az = 0 .
Bx = |
x |
, By = |
y |
, Bz = 0 . |
x 2 + y 2 |
x2 + y2 |
1.15. Найти ротор и дивергенцию следующих векторных полей, заданных в декартовой системе координат:
A = cos(ay)1x +sin(ax)1y +tg(az)1z ,
B = 6x1x + 5z1y +10 y1z .
Ответ: rot A = a(cos(ax)+ sin(ay))1z , div A = a/cos2(az), rot B = 5 1z , div B = 6 .
1.16.Используя правила действия с оператором Гамильтона, доказать тождество
rot[AB] = (B )A −(A )B + AdivB −BdivA .
1.17.В пространстве заданы два векторных поля А и В. Найти выражение для поля С = grad (АВ).
Указание: Выразить операцию grad через оператор и воспользоваться правилом дифференцирования произведения.
Ответ: C = [Arot B] + [B rot A] +(B ) A+(A ) B .
1.18. Доказать следующие тождества векторного анализа (ϕ и А — произвольные дифференцируемые скалярное и векторное поля):
div rot A =0 ,
rot grad ϕ = 0 ,
rot (ϕ A) =[grad ϕ A]+ϕ rot A , div (ϕ A) = grad ϕ A+ϕ div A , grad (ϕ1ϕ2 ) =ϕ1 grad ϕ2 +ϕ2 grad ϕ1 .
1.19. Векторное поле А обладает единственной составляющей Ax, которая постоянна в пределах плоского слоя толщиной 2d:
|
0, |
( y < d), |
|
||
Ax = A0 |
, (d ≥ y ≥ −d), |
|
|
0, |
(y < −d). |
|
||
Найти выражение ротора поля.
Ответ: rotA = A0 [δ(y - d) -δ(y +d)]1z , где δ (у) — функция Дирака.
