Глава 8. Собственные значения и собственные векторы матрицы.

В этой главе рассматриваются вопросы о собственных векторах и собственных значениях произвольной квадратной матрицы, симметрической матрицы и подобных матриц.

1. Основные понятия.

Определение. Вектор , называетсясобственным вектором квадратной матрицы , если существует такое число, что

. При этом числоназываетсясобственным значением матрицы , соответствующим собственному вектору.

Уравнение может быть записано в виде

.

Определение. Если - собственное значение матрицы, асоответствующий ему собственный вектор, тоназываютсобственной парой матрицы .

● Пример 1. Показать, что вектор является собственным вектором матрицы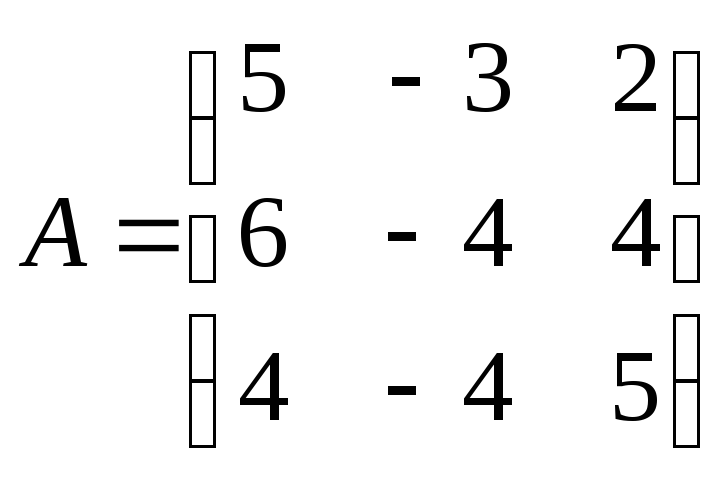. Найти соответствующее ему собственное значение.

Решение.

Так как 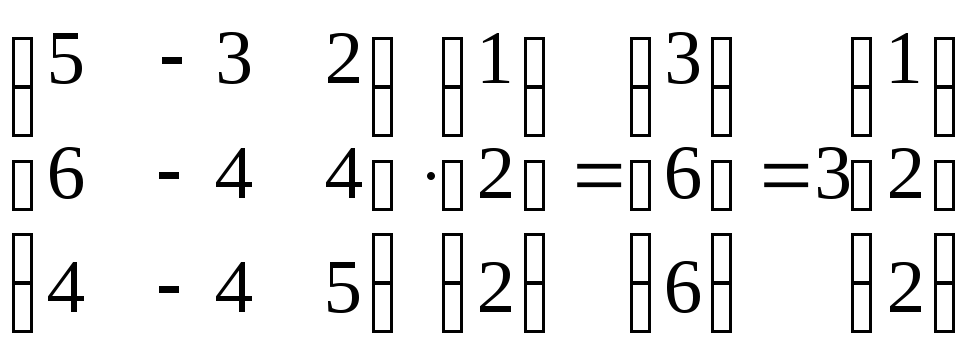(), то- собственный вектор матрицы, соответствующий собственному значению.●

● Пример 2. Показать, что если - собственная пара матрицы, то- собственная пара матрицы.

Решение. Действительно,

, т.е. . Из последнего следует, что- собственная пара матрицы.●

● Пример 3. При каких ивекторявляется собственным вектором матрицы?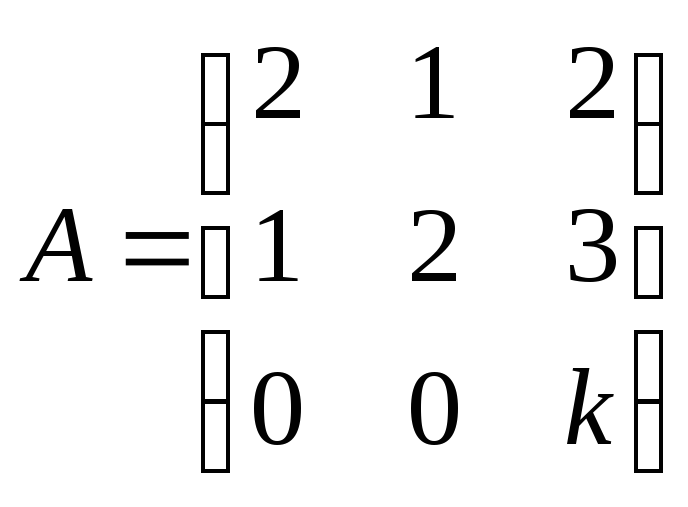

Решение. Найдем вектор ..

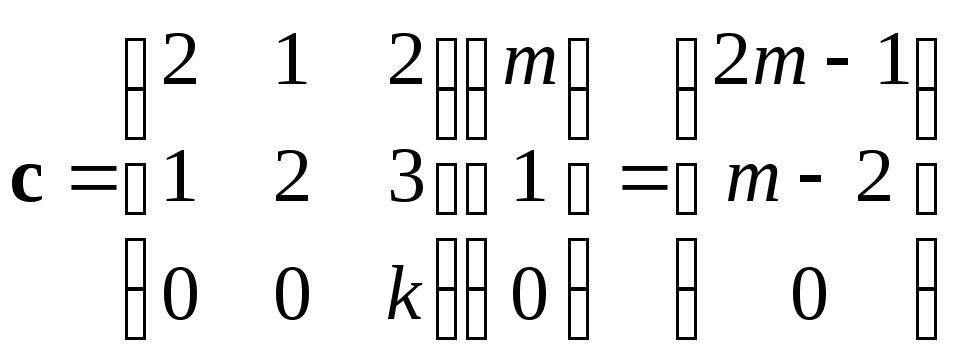Если - собственный вектор матрицы , то, откуда. Из последнего имеемии.

Ответ: при и произвольномвекторсобственный вектор матрицы.

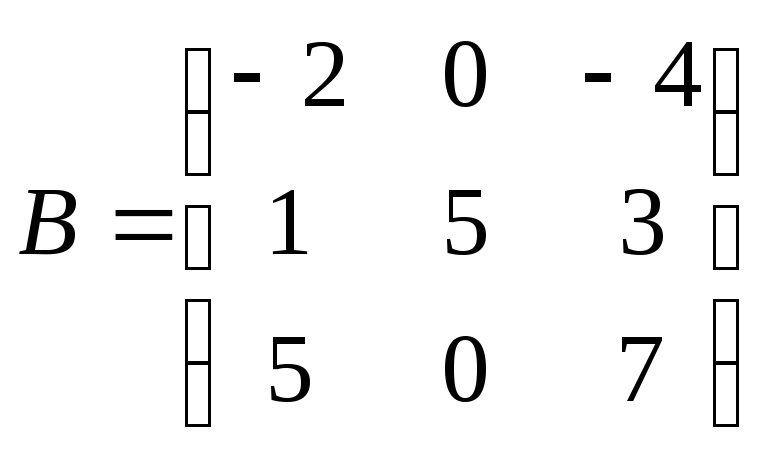● Пример 4. Существует ли , при котором- собственный вектор матрицы? Если существует, указать соответствующую собственную пару.

Решение. Вычислим произведение

Если - собственная пара матрицы, то

.

Из последнего равенства имеем 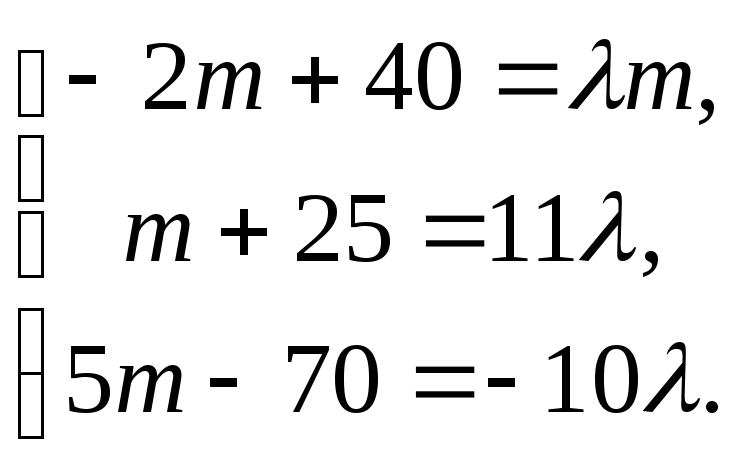Откуда,,.

- собственная пара матрицы.●

2. Свойства собственных векторов.

1) Если - собственный вектор матрицы , а- соответствующее ему собственное значение, то при любомвектортакже является собственным вектором этой матрицы, соответствующим этому же собственному значению.

►Действительно, .◄

Замечание. Любой собственный вектор матрицы определяет целое направление собственных векторов этой матрицы с одним и тем же собственным значением.

2) Собственные векторы матрицы, соответствующие различным её собственным значениям, линейно независимы.

►Доказательство. Пусть и- собственные пары матрицы, где.

Предположим, что илинейно зависимые векторы.

Если илинейно зависимы, то хотя бы один из этих векторов можно представить в виде линейной комбинации другого (пусть).

Тогда , откуда следует, что. Так как, то.

Полученное противоречие доказывает утверждение.◄

3) Если илинейно независимые собственные векторы матрицы, соответствующие одному и тому же собственному значению, то любая нетривиальная линейная комбинация этих векторов() также является собственным вектором этой матрицы, соответствующим этому же собственному значению.

►Действительно, , что и требовалось доказать.◄

4) Если матрица диагональная , то ее собственные значения совпадают с диагональными элементами этой матрицы (), а единичный векторявляется собственным вектором, соответствующим собственному значению.

►Действительно, ◄

3 Нахождение собственных значений и собственных векторов.

Собственные значения и собственные векторы матрицы удовлетворяют матричному уравнению.

Если собственный вектор матрицы , то однородная системаимеет нетривиальное решение, поэтому(порядок матрицыи. Последнее уравнение позволяет найти собственные значения матрицы.

Определение. Многочлен называютхарактеристическим многочленомматрицы.

Определение. Уравнение

называется характеристическим уравнением матрицы .

Корни характеристического уравнения матрицы являются собственными значениями матрицы.

Характеристическое уравнение матрицы может быть записано в виде.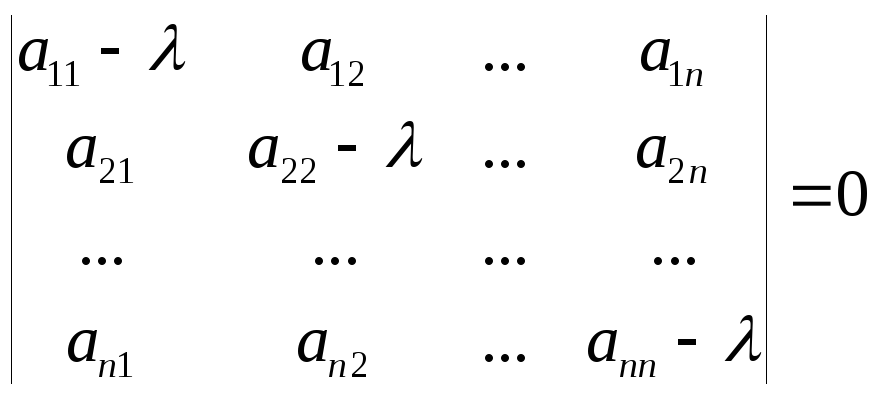

Определение. Множество всех собственных значений квадратной матрицы называется спектром этой матрицы.

Спектр матрицы -го порядка содержитсобственных значений матрицы, которые могут быть как действительными, так и комплексными, простыми так и кратными.

Для матрицы характеристическое уравнениеможет быть может быть преобразовано к виду .

, поэтому характеристическое уравнение матрицы 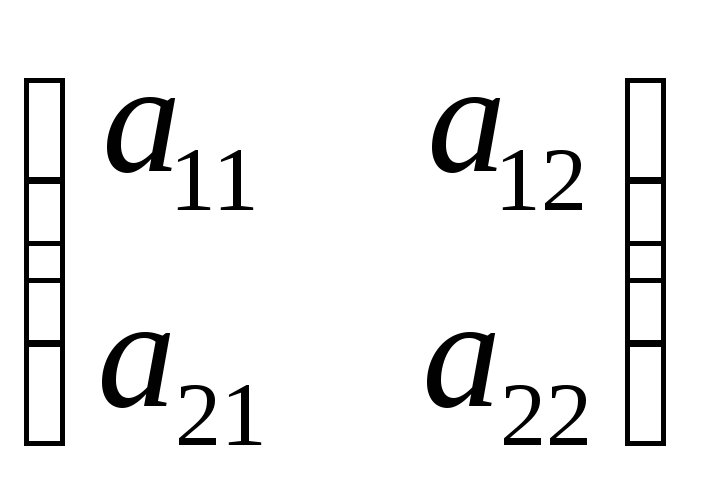имеет вид

. (8.1)

При этом

,(8.2)

.(8.3)

Уравнение 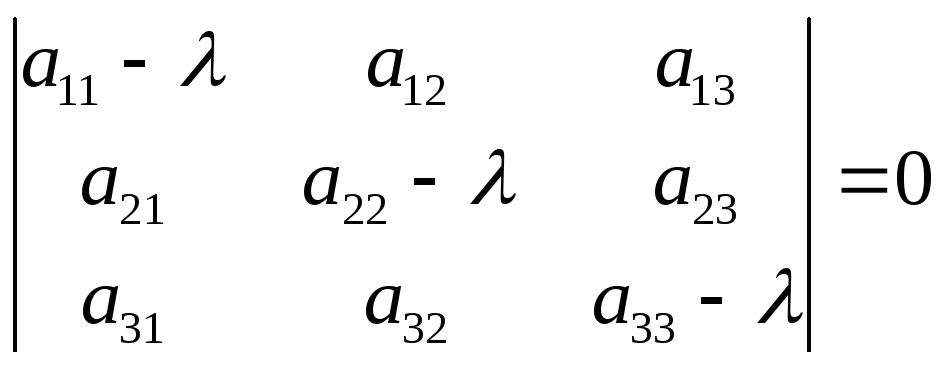является характеристическим уравнением матрицы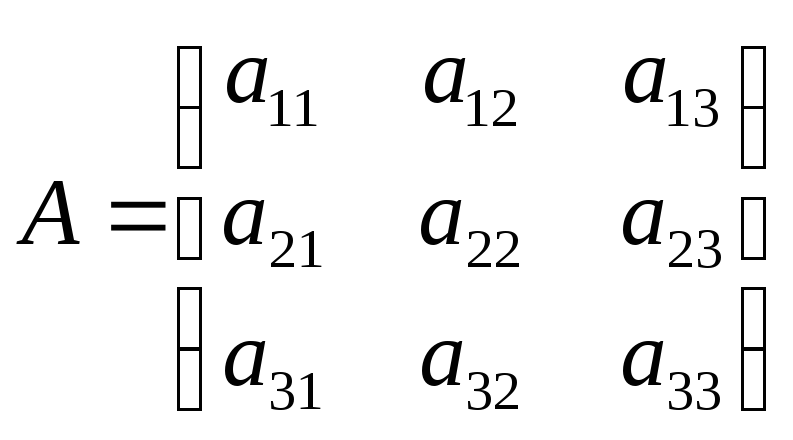.Это уравнение может быть представлено в виде

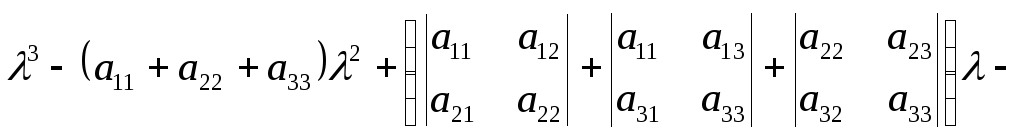
или

, (8.4)

где , аминоры определителя.

Если ,икорни характеристического уравнения (8.4), то это уравнение может быть записано в виде

. (8.5)

Сравнивая уравнения (8.4) и (8.5), можно записать следующее:

,(8.6)

,(8.7)

.(8.8)

Собственные векторы матрицы , соответствующие собственному значению, удовлетворяют матричному уравнению, которое может быть записана в форме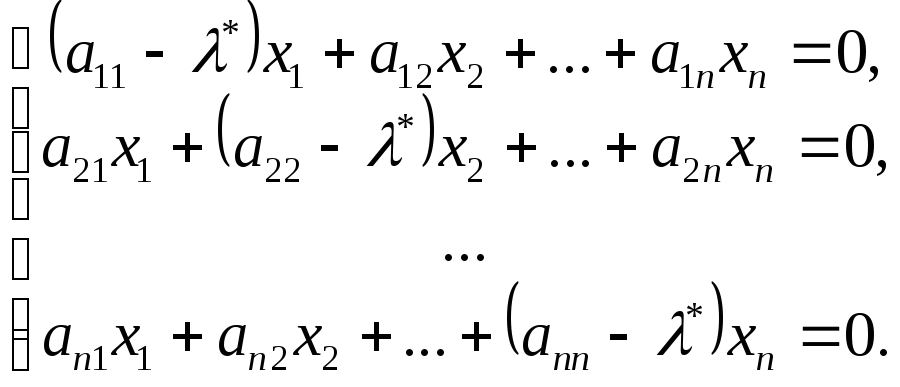Так как ранг матрицы этой системы меньше числа неизвестных (=0), то система имеет бесконечное множество

решений, каждое ненулевое из которых является собственным вектором, соответствующим собственному значению .

● Пример 5. Найти собственные значения и собственные векторы матрицы .

Решение. - характеристическое уравнение для данной матрицы, откуда,и.

Для нахождения собственных векторов, соответствующих собственному значению , имеем системуэквивалентную уравнению. Векторявляется решением этого уравнения, а привектор- искомый собственный вектор.

Для нахождения собственных векторов, соответствующих собственному значению , имеем системуиз которой следует, что векторприявляется собственным вектором, соответствующим собственному значению.

Ответ. ,при;,при.

● Пример 6.

Найти собственные пары матрицы .

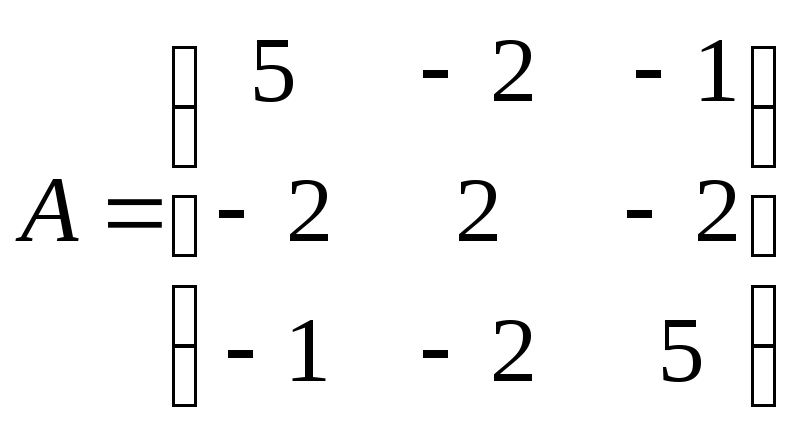Решение. 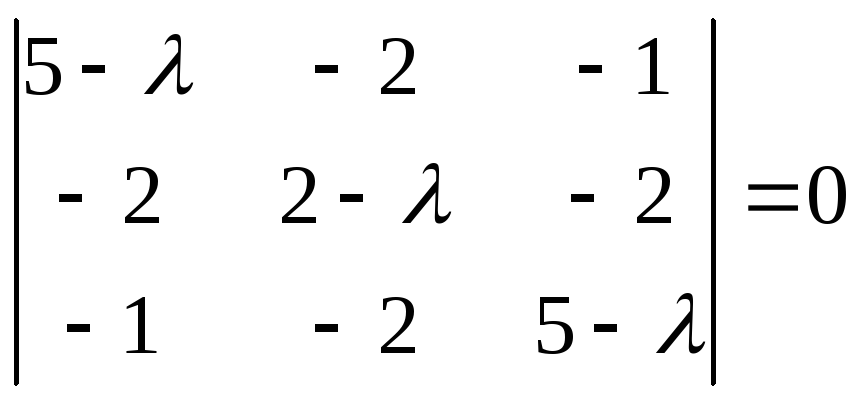- характеристическоеуравнение матрицы , которое может быть записано в виде, где,,,,(проверьте).

- характеристическое уравнение матрицы , корни которого.

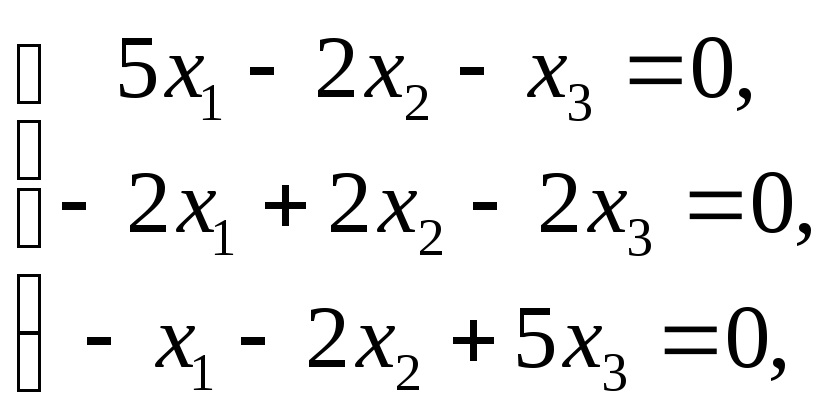Собственные векторы, соответствующие собственному значению , находим из системы. Приимеем систему которая равносильна системе 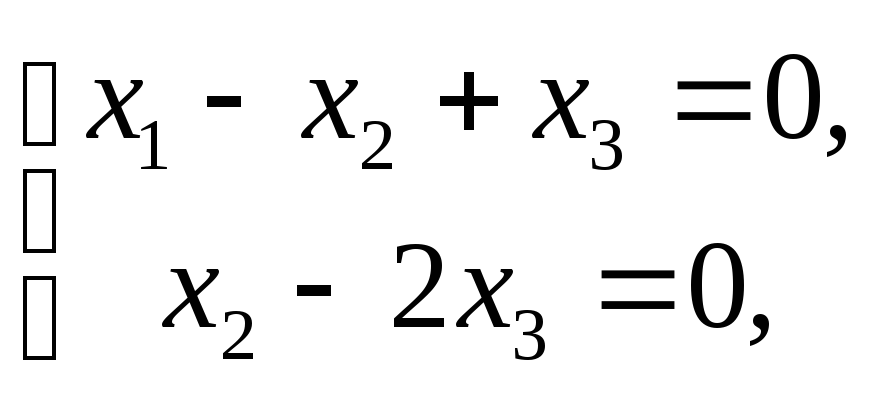решение которой .

При векторявляется собственным вектором матрицы, соответствующим собственному значению.

При для нахождения собственных векторов имеем систему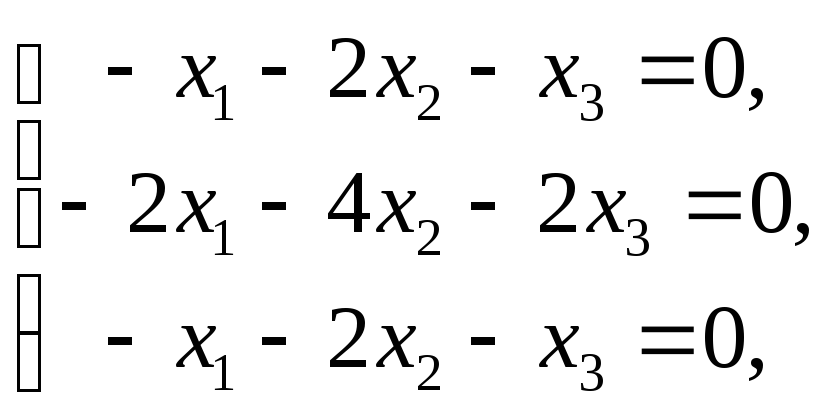которая равносильна одному уравнению.

При любых ивекторесть решение уравнения, а при

является собственным вектором, который соответствует собственному значению .

Ответ: при;при.

● Пример 7. Найти собственные значения и собственные векторы матрицы .

Решение. Характеристическое уравнение для указанной матрицы имеет вид , откудаи.

Для нахождения собственных векторов, соответствующих собственному значению , имеем системуиз которой следуетпри.

Для нахождения собственных векторов, соответствующих собственному значению , имеем системуиз которой следуетпри.

Ответ. ,при;,при.

● Пример 8.

Доказать, что если собственная пара невырожденной матрицы , то -собственная пара матрицы .

►Так матрица невырожденная (), то существует. Произведение собственных значений матрицыравно, а так как, то собственное значение.

- собственная пара матрицы , поэтому.Умножив последнее равенство слева на , имеем, откуда,и. Последнее равенство означает, что - собственная пара матрицы .◄