Дискретка_Экзамен_Ответы / комб / 2 Сочетания
.docx
2.7. Сочетания
Сочетанием из n элементов по k называется k-элементное подмножество n-элементного множества.
Теорема 2.5.
Количество всех различных сочетаний
из n
элементов по k
определяется формулой
.
Доказательство.
Можно получить все
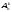размещений,
упорядочив всеми возможными способами
каждое из
сочетаний. Количество способов
упорядочивания одного сочетания равно
k!,
следовательно
=
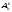k!
. Отсюда
.
Пусть элементами множества М являются натуральные числа от 1 до n. Для сокращения записи такое множество будем обозначать {1..n}.
Например,
сочетания из шести элементов по три
(
),
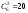в возрастающем лексикографическом
порядке запишутся следующим образом:
123 135 234 256
124 136 235 345
125 145 236 346
126 146 245 356
134 156 246 456
Алгоритм 2.5 порождения сочетаний из n элементов по k.
Вход: i – заполняемое место в сочетании С;
b – минимальный элемент, который можно поставить на i-ое место.
Выход: последовательность всех сочетаний из n элементов по k в возрастающем лексикографическом порядке.
Глобальные параметры: С – формируемое сочетание;
n – мощность множества.
k – количество элементов в сочетании.
Сочетание(i, b)
Ci := x
i=k
x{b..n-k+i}
+
С
Сочетание (i+1, x+1)
Конец
Рис.2.11. Рекурсивный алгоритм порождения сочетаний
из n элементов по k
Пусть задано множество {1,2,3,4,5} и требуется получить все его сочетания по 3.
сочетание
3 {1,2,3)
множество
{3,4,5}
4 сочетание
сочетание
{1,2,4)
{1,2,?} 5
2 сочетание
{1,2,5)
множество
множество 7
сочетание
{2,3,4} 6 {4,5} {1,3,4)
сочетание
сочетание 8
{1,?,?}
{1,3,?}
сочетание
9 {1,3,5)
1 множество
{5} 10 сочетание
сочетание
{1,4,5)
множество {1,4,?}
{1,2,3}
сочетание
11 множество
13 сочетание
{?,?,?}
12 {4,5}
{2,3,4)
множество
сочетание 14
{3,4} {2,3,?} сочетание
сочетание
15
{2,3,5)
17 {2,?,?} множество
{5} 16 сочетание
сочетание
{2,4,5)
{2,4,?}
множество множество
{4} 18 {5} 19 сочетание
сочетание
сочетание
{3,4,5)
{3,?,?} {3,4,?}
Рис.2.12. Схема получения всех сочетаний по алгоритму 2.5