Дискретка_Экзамен_Ответы / булевы / 5 скобочная минимизация булевых функций

5.6.3. Скобочная минимизация булевых функций

Скобочная минимизация булевых функций (факторизация) в ряде случаев позволяет получить скобочную форму, значительно более простую, чем минимальная ДНФ. Процесс факторизации заключается в многократном выполнении операции вынесения за скобки общих членов. Работу факторного алгоритма рассмотрим на примере.

Пусть минимальная ДНФ функции f имеет вид:

Обозначим каждую элементарную конъюнкцию буквами А, В, С, D. Тогда функцию f можно представить множеством: F = (A, B, C, D).

На первом этапе работы алгоритма ищутся все попарные пересечения элементов множества F. B нашем случае имеем:

AB=x₁; AC=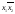; AD=;

BC=x₁; BD=x₁x₅; CD=.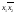

Выбирается та пара элементов множества F, пересечение которых дает конъюнкцию наибольшей длины. Для рассматриваемого примера выберем либо пару (А, С), либо (А, D), либо (C, D), что с точки зрения результатов работы алгоритма безразлично. Выберем пару (C, D) и запишем функцию f аналитически, вынося общий элемент за скобки по отношению к C и D. Получим:

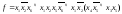
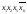Обозначим A₁=; B₁=; C₁=.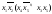

Получим F₁=(A₁, B₁, C₁).

На втором этапе алгоритма ищутся все попарные пересечения элементов множества F₁. В нашем случае имеем:

A₁B₁=x₁; A₁C₁=; B₁C₁=x₁.

Вновь выбирается пара элементов множества F₁, пересечение которых дает конъюнкцию наибольшей длины. Выберем пару (A₁, C₁) и запишем функцию f аналитически, вынося общий элемент за скобки по отношению к A₁ и C₁. Получим:

.

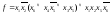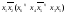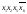Обозначив А₂=, В₂=, получим множест-во F₂=(A₂, B₂). Ищем пересечение элементов множества F₂. Получаем A₂B₂=x₁. Окончательно имеем:

.
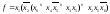