
Билеты по математике / Билет 17
.pdf
Билет 17
1. Расстояние от точки до прямой – определение.
Расстояние от точки до прямой определяется через расстояние от точки до точки. Покажем как это делается.
Пусть на плоскости или в трехмерном пространстве задана прямая a и точка M1, не лежащая на прямой a. Проведем через точку M1 прямую b, перпендикулярную прямой a. Обозначим точку пересечения прямых a и b как H1. Отрезок M1H1 называется перпендикуляром, проведенным из точки M1 к прямой a.
Определение.
Расстоянием от точки M1 до прямой a называют расстояние между точками
M1 и H1.
Однако чаще встречается определение расстояния от точки до прямой, в котором фигурирует длина перпендикуляра.
Определение.
Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.
Это определение эквивалентно первому определению расстояния от точки до прямой.
Обратите внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.
Возьмем на прямой a точку Q, не совпадающую с точкой M1. Отрезок M1Q называют наклонной, проведенной из точки M1 к прямой a. Нам нужно показать, что перпендикуляр, проведенный из точки M1 к прямой a, меньше любой наклонной, проведенной из точки M1 к прямой a. Это действительно так: треугольник M1QH1 прямоугольный с гипотенузой M1Q, а длина гипотенузы
всегда больше длины любого из катетов, следовательно,  .
.

К началу страницы
Расстояние от точки до прямой на плоскости – теория, примеры, решения.
В зависимости от исходных данных для нахождения расстояния от точки до прямой можно использовать различные методы геометрии: теорему Пифагора, определения синуса, косинуса, тангенса угла, признаки равенства и подобия треугольников и т.п. Множество подобных задач решается на уроках геометрии в средней школе.
Если же при нахождении расстояния от точки до прямой есть возможность ввести прямоугольную систему координат, то можно воспользоваться методом координат. В этом пункте статьи мы подробно остановимся на двух способах нахождения расстояния от точки M1 до прямой a, которые заданы в прямоугольной декартовой системе координат Oxy на плоскости. В первом случае расстояние от точки M1 до прямой a мы будем искать как расстояние от точки M1 до точки H1, где H1 – основание перпендикуляра, опущенного из точки M1 на прямую a. Во втором способе нахождения расстояния от точки M1 до прямой a будем использовать нормальное уравнение прямой a.
Итак, поставим перед собой следующую задачу: пусть на плоскости зафиксирована прямоугольная система координат Oxy, задана точка  ,
,
прямая a и требуется найти расстояние  от точки M1 до прямой a. Разберем по-очереди два способа ее решения.
от точки M1 до прямой a. Разберем по-очереди два способа ее решения.
Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.
Если мы определим координаты  точки H1, то искомое расстояние
точки H1, то искомое расстояние  мы сможем вычислить, используя формулу для нахождения расстояния от точки
мы сможем вычислить, используя формулу для нахождения расстояния от точки
M1 до точки H1 по их координатам:  .
.
Осталось разобраться с нахождением координат точки H1.

Мы знаем, что прямой линии в прямоугольной системе координат Oxy соответствует некоторое уравнение прямой на плоскости. Будем считать, что способ задания прямой a в условии задачи позволяет написать общее уравнение прямой a или уравнение прямой с угловым коэффициентом. После этого мы можем составить уравнение прямой, проходящей через заданную точку M1 перпендикулярно заданной прямой a. Обозначим эту прямую буквой b. Тогда точка H1 – это точка пересечения прямых a и b, следовательно, координаты точки H1 можно определить, обратившись к материалу статьи координаты точки пересечения двух прямых.
Итак, мы получили алгоритм для нахождения расстояния от заданной точки  до заданной прямой a:
до заданной прямой a:
находим общее уравнение прямой a вида 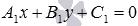 или уравнение прямой a с угловым коэффициентом
или уравнение прямой a с угловым коэффициентом  ;
;
получаем общее уравнение прямой b вида  или уравнение прямой b с угловым коэффициентом вида
или уравнение прямой b с угловым коэффициентом вида  ,
,
учитывая, что прямая b проходит через заданную точку M1 и перпендикулярна заданной прямой a;
определяем координаты  точки H1 - точки пересечения прямых a и
точки H1 - точки пересечения прямых a и
b, решая систему линейных уравнений |
или |
;
вычисляем требуемое расстояние от точки M1 до прямой a по формуле
.
Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.
Следующая теорема отвечает на вопрос: «Как найти расстояние от заданной точки до заданной прямой на плоскости»?
Теорема.
В прямоугольной системе координат Oxy на плоскости расстояние от точки
 до прямой a, заданной нормальным уравнением прямой вида
до прямой a, заданной нормальным уравнением прямой вида
 , равно модулю значения выражения, находящегося в левой части нормального уравнения прямой, вычисленного при
, равно модулю значения выражения, находящегося в левой части нормального уравнения прямой, вычисленного при  ,
,
то есть,  .
.
Доказательство.

Так как прямой a в прямоугольной системе координат Oxy на плоскости соответствует нормальное уравнение прямой  , то
, то
 - нормальный вектор прямой a единичной длины, а расстояние от начала координат до прямой a равно p единиц. Изобразим эти
- нормальный вектор прямой a единичной длины, а расстояние от начала координат до прямой a равно p единиц. Изобразим эти
данные на чертеже, а также добавим точку  , радиус-вектор точки М1 -
, радиус-вектор точки М1 -
 , построим искомое расстояние от точки М1 до прямой a -
, построим искомое расстояние от точки М1 до прямой a -  , покажем проекции М2 и H2 точек М1 и H1 соответственно на прямую,
, покажем проекции М2 и H2 точек М1 и H1 соответственно на прямую,
проходящую через точку O и имеющую направляющий вектор 
, обозначим числовую проекцию вектора  на направление вектора
на направление вектора
 как
как  .
.
В зависимости от расположения точки М1 относительно прямой a возможны следующие варианты.

Все полученные результаты можно описать одной формулой:
. Осталось привести полученное равенство к виду
 , то есть показать, что
, то есть показать, что
 .
.
Определение скалярного произведения векторов дает нам равенство
 , а это же самое скалярное произведение в координатной форме имеет вид
, а это же самое скалярное произведение в координатной форме имеет вид
, следовательно,
 . Тогда
. Тогда

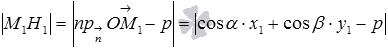 , что и требовалось доказать.
, что и требовалось доказать.
Таким образом, чтобы найти расстояние от точки  до прямой a на плоскости нужно:
до прямой a на плоскости нужно:
|
получить |
нормальное |
уравнение |
прямой |
a |
в |
виде |
|
|
|
(если оно сразу не дано); |
|
|
|
|
|
вычислить |
значение выражения |
|
- |
полученное |
||
|
значение является искомым расстоянием |
. |
|
|
|
||
2 Таблица основных неопределённых интегралов [править]

