
Билеты по математике / Билет 18
.pdf
Билет 18
1. Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
,
где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению
и
Канонический вид[править]
Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду
 ,
,
где a и b — полуоси[источник не указан 194 дня].
Полярные координаты[править]
График гиперболы в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то
Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то
Параметризация ветви гиперболы с помощью гиперболических функций
Уравнения в параметрической форме[править]
Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции[1].
В первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви.
Свойства[править]

Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
o Иначе говоря, если  и
и  фокусы гиперболы, то касательная в
фокусы гиперболы, то касательная в
любой точки  гиперболы является биссектрисой угла
гиперболы является биссектрисой угла  .
.
Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при  .
.
Асимптоты[править]
Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1
Для гиперболы, заданной в каноническом виде
уравнения двух асимптот имеют вид:
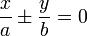 .
.

Диаметры и хорды[править]
Диаметры гиперболы
Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
Угловой коэффициент  параллельных хорд и угловой коэффициент
параллельных хорд и угловой коэффициент  соответствующего диаметра связан соотношением
соответствующего диаметра связан соотношением
Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
Определение центра гиперболы по её графику
Касательная и нормаль[править]
Поскольку гипербола является гладкой кривой, в каждой её точке (x0, y0) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:
 ,
,

или, что то же самое,
.
Вывод уравнения касательной
Уравнение касательной произвольной плоской линии имеет вид
Каноническое уравнение гиперболы можно представить в виде пары функций
 .
.
Тогда производная этих функций имеет вид
.
Подставив это уравнение в общее уравнение касательной, получим
Уравнение нормали к гиперболе имеет вид:
.
Вывод уравнения нормали
Уравнение нормали произвольной плоской линии имеет вид
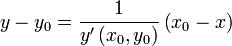 .
.
Каноническое уравнение гиперболы можно представить в виде пары функций
 .
.
Тогда производная этих функций имеет вид

.
Подставив это уравнение в общее уравнение нормали, получим
 .
.
2.
Преобразование интегралов
Интегрирование по частям
или
(u, v непрерывно дифференцируемы на интервале 
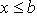 ).
).
Замена переменного (интегрирование подстановкой)
Если функция x = x(u) непрерывно дифференцируема на интервале 
 , а функция f(x) непрерывна на интервале
, а функция f(x) непрерывна на интервале 
 , где m - точная нижняя, а M - точная верхняя граница функции x(u) на интервале
, где m - точная нижняя, а M - точная верхняя граница функции x(u) на интервале 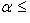
 , то
, то
