Билеты по математике / Билет 3

БИЛЕТ № 3

1. Определитель n-го порядка.

Определитель n-го порядка есть сумма n! членов каждый из которых соответствует одному из n! упорядоченных множеств полученных r попарными перестановками элементов из множества

1,2,…,n.

Замечание 1. Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.

Замечание 2. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.

Пример 2.14. Вычислить определитель n-го порядка.

Решение. Рассмотрим определитель диагональной матрицы А

Искомый определитель Dn получается прибавлением к каждому элементу определителя матрицы

Осталось вычислить сумму алгебраических дополнений всех элементов матрицы. Заметим, что алгебраическое дополнение недиагонального элемента равно нулю ( Aij при i не равном j , так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.

Поэтому:

2.Производная от функций, заданных неявно и в параметрическом виде.

Производные от функций, заданных параметрически:

Пусть задана зависимость двух переменных 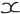и от параметра , изменяющегося в пределах о до :

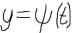Пусть функция имеет обратную: . Тогда мы можем, взяв композицию функций и от величины , получить зависимость от Х:

. Зависимость величины У от величины Х , заданная через зависимость каждой из них от параметра в виде: , называется функцией Y=Y(X) , заданной параметрически. Производную функции , заданной параметрически, можно выразить через производные функций и : поскольку и, по формуле производной

обратной функции, , то , где -- значение параметра, при котором получается интересующее нас при вычислении производной значение х.

Заметим, что применение формулы приводит нас к зависимости между и , снова выраженной в виде параметрической зависимости: , 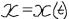; второе из этих

соотношений -- то же, что участвовало в параметрическом задании функции . Несмотря на то, что производная не выражена через х в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра.

Производные функций, заданных неявно:

Если независимая переменная х и функция у связаны уравнением вида, которое не разрешено относительно у, то функция у называется неявной функцией переменной.

Всякую явно заданную функцию можно записать в неявном виде . Обратно сделать не всегда возможно.

Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию как функцию от , а затем из полученного уравнения найти производную .