Билеты по математике / Билет 22

22

Базис на плоскости и в пространстве.

Определение. Базисом на плоскости называются два любых линейно независимых вектора.

Из теоремы 2 (см. п. 4) следует, что два любых неколлинеарных вектора образуют базис. Пусть любой вектор на плоскости, а векторы и образуют базис. Так как на плоскости всякие три вектора линейно зависимы, то вектор линейно выражается через векторы базиса, т. е. выполняется соотношение

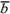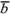относительно базиса и 1 . Разложение вектора по и 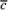является единственным

Доказательство. Допустим, что наряду с разложением (3) имеет место разложение

Покажем, что в этом случае 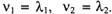Действительно, вычитая равенство (4) из равенства (3), получаем соотношение

(Возможность почленного вычитания равенств (4) и (3) и производимой группировки членов вытекает из свойств линейных операций над

Определение. Базисом в пространстве называются три любых линейно независимых вектора.

Из теоремы 2 (см. п. 5) следует, что три любых некомпланарных вектора образуют базис. Как и в случае плоскости, устанавливается, что любой вектор разлагается по векторам , и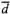

причем это разложение единственное.

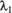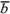Числа , , называют координатами вектора в пространстве относительно базиса , и .

Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными линейными

координаты умножаются на это число. Доказательство. Пусть, например,

.

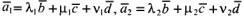Тогда в силу свойств линейных операций (см. п. 2)

В силу единственности разложения по базису ,, теорема для этого базиса доказана.

Экстремумы функции

Определение 1. Точка называется точкой максимума [точкой минимума]

функции , если существует такая - окрестность точки , что для всех значений из этой окрестности выполняется неравенство .

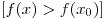Определение 2. Значение функции в точке максимума (точке минимума)

называетсямаксимумом (минимумом) функции .

Определение 3. Точки минимума и точки максимума называются точками экстремумафункции , а значения функции в этих точках —

экстремумами функции .

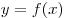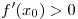Теорема 1. Если функция непрерывна в точке , а на промежутке и на промежутке , то является точкой максимума функции .

Теорема 2. Если функция 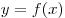непрерывна в точке , а на промежутке и на промежутке , то — точка минимума функции .

Теорема 3 (Ферма). Пусть функция определена в некоторой окрестности точки и дифференцируема в этой точке. Если — точка экстремума функции , то .

Теорема 4. Пусть функция дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки 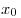, и непрерывна в точке . Тогда, если меняет знак с «» на «» (с «» на «») при переходе через точку , то — точка минимума (точка максимума) функции .