Билеты по математике / Билет 16

Билет 16

1. 2.4. Скалярное произведение векторов и его свойства

Определение 1. Скалярным произведением двух ненулевых векторов называется число, равное произведению модулей векторов - сомножителей на косинус угла между ними.

. (2.6)

Спроектируем вектор на вектор

,

тогда

.

Определение 2. Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию второго вектора на первый.

Рассмотрим свойства скалярного произведения.

1. .

2. .

Доказательство.

.

3. ,

где - константа.

Доказательство.

,

т.е. скалярный множитель выносится за знак скалярного произведения. Если векторы

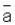и

коллинеарны, то угол между ними = 0 или = 180 , а cos = 1. Поэтому

.

В частности,

.

Выражение

называется скалярным квадратом вектора a и

.

Скалярный квадрат вектора равен квадрату его модуля.

Если один из векторов скалярного произведения равен нулю, то скалярное произведение равно нулю.Если отличные от нуля векторы и ортогональны, то их скалярное произведение равно нулю.

. (2.7)

Действительно, если

,

то угол= 90 и cos90 , следовательно,

.

Если скалярное произведение двух векторов

и ,

отличных от нуля, равно нулю, то векторы ортогональны. Действительно, если ( , ) = 0, но

то cos = 0, а это значит, что = 90 и . Таким образом, это условие является необходимым и достаточным условием ортогональности двух векторов.

Скалярное произведение ортов , ,

Так как

, ,

единичные векторы, то

, ,

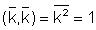. (2.8)

А так как они попарно ортогональны

то ( , ) = 0, ( , ) = 0, ( , ) = 0. (2.9)

Наиболее просто скалярное произведение векторов вычисляется в декартовом базисе.Пусть векторы

и

заданы своими координатами

и

.

Используя свойства скалярного произведения, находим

.(2.10)

Таким образом, в декартовом базисе скалярное произведение равно сумме произведений соответствующих координат. Это утверждение позволяет вывести ряд формул.

. (2.11)

Вычислим угол между векторами

и

; (2.12)

. (2.13)

Необходимое и достаточное условие ортогональности векторов

и

определяется следующим равенством : x1x2 +y1y2 +z1z2 = 0 (2.14)

2. Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или

Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле

В случае сложной функции y = f(u), u = g(x) аргумент u функции y называют промежуточным аргументом в отличие от независимой переменной x. Тогда правило дифференцирования сложной функции можно сформулировать так: производная сложной функции равна произведению производной этой функции по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x.

огари и еская производная — производная от натурального логарифма функции.

Часто применяется для упрощения нахождения производной некоторых функции, например сложно-показательных

Производная сложно-показательной функции [править]

Производная произведения функций [править]

.

Можно расписать формулу и прийти к другой форме: