Билеты по математике / Билет 14

Билет 14

1.Вектором называется направленный отрезок. Если у отрезка AB его концы равноправны, то для вектора один из концов отрезка, например, A называется началом, а другой, то есть B, – концом. Обозначим вектор либо указанием концов отрезка, причем начало вектора ставится на первое место, либо строчной латинской буквой со стрелкой или чертой над буквами.

Углом между ненулевыми векторами и называется угол BAC. Углом между

любыми двумя ненулевыми векторами и называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю.

Нулевым вектором называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.

Замечание 11.1

Любую пару векторов, один из которых равен нулевому вектору будем считать коллинеарными.

Теорема 11.1.

Два вектора, сонаправленные с третьим вектором, сонаправлены.

Доказательство

Рисунок 11.1.6. К теореме 11.1

Свойства равенства векторов:

каждый вектор равен самому себе;

если вектор равен вектору то равен

два вектора, равные третьему, равны.

Теорема 11.2.

Пусть даны два вектора и не лежащие на одной прямой. Соединим начала A и C и концы B и D этих векторов. Если четырехугольник ABDC – параллелограмм, то

и наоборот, если то четырехугольник ABDC – параллелограмм.

Доказательство

Рисунок 11.1.7. К теореме 11.2

Теорема 11.3.

Если то

Доказательство

Рисунок 11.1.8. К теореме 11.3

Пусть на плоскости Oxy точка – начало вектора а точка – его конец.

Координатами вектора 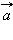называются числа Для обозначения того, что вектор имеет координаты и используют запись Длина отрезка

.

3. Таблица производных

1. .( Un)'= n· Un–1· U'.

Следствие: (х) '=1.

2. ( au)'=au· lna· U'.

Следствие: (еu)'=euu'.

3. .

Следствие: .

4.(sinU)'=cosU·U'.

5.(cosU)'=–sinU·U'.

6. .

7. .

8. .

9. .

10. .

11. .

Пример. Найти производные заданных функций:

1) .

Решение. Применим формулу , здесь n=3,

. Тогда . Найдем U'.

Следовательно, .

2) .

Решение. Преобразуем сначала данную функцию, а затем найдем производную этой функции:

.

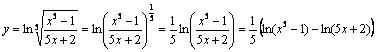Тогда .

Для нахождения производных и применим

формулу: . Получим:

Для нахождения производной применим формулу

. Тогда

Следовательно, . 4) .

Решение. . Найдем: по формуле ( au)'=au· lna· U'.

Будем иметь .

Производную (х2cos2x)' найдем по формуле (U·υ)'=U'υ+Uυ'и

(cosU)'= -sinU*U'. Тогда

Следовательно, .

Пример. Вычислить приближенное значение , заменив в точке х=243 приращение функции дифференциалом.

Решение. Имеем: .

В нашем примере х=243, х+∆х=252, тогда ∆х=252–243=9,

.

Отсюда

Поэтому .

Следовательно, .

4. Функции нескольких переменных

Определение. Переменная z называется функцией переменных х и у, если каждой паре значений х и у в некоторой области их изменения поставлено в соответствие одно значение z. Функциональную зависимость z от х и у записывают в виде: z=f(x,у). Это уравнение определяет некоторую поверхность в

параболоид. Пусть z=a, тогда x2+y2=a, т.е. линия пересечения плоскости z= a с поверхностью z=x2+y2 есть окружность x 2+ y 2= a

радиуса . Пусть у=0, тогда z=x2 и, следовательно, при пересечении плоскости Oхz с поверхностью получается парабола. Метод сечений дает возможность лучше представить себе геометрический образ данной функции.

Определение. Число А называется пределом функции z=f(x,у) в точке М0(х0, у0), если для каждого числа ε>0 найдется такое число β>0, что для всех точек М(х,у), для которых выполняется неравенство |ММ0|<β, будет выполняться неравенство | f(x,у)– A|<

ε

точке М0(х0,у0), если имеет место равенство .

5. Частные производные и полный дифференциал 1-го

порядка

Определение. Производная от функции z=f(x,у) по х, найденная в предложении, что у остается постоянным, называется

частной производной от z по х и обозначается или f'x (x,у). Аналогично определяется и обозначается частная производная z по

у.

Если функция z=f(x,у) имеет в точке (х,у) непрерывные частные производные, то ее полное приращение может быть

полного приращения z и называется полным дифференциалом

Производная найдена в предположении, что у постоянна, а

найдена в предположении, что х постоянна. По формуле (3):

.

Ответ. dz=(10 x–6xy3) dx+(9 x2 y2+6) dy.