Билеты по математике / Билет 27

БИЛЕТ № 27

1.Проекции вектора на ось, их свойства.

Пусть на плоскости или в пространстве заданы ось l с единичным вектором е и произвольный вектор а.

Ортогональной проекцией (или просто проекцией) вектора а на ось l называется число, равное произведению длины вектора а на косинус угла между векторами е и а.

Проекция вектора а на ось l обозначается символом прl а или пре а. Таким образом, по определению

прl а = | a | cos .

Отложим вектор а от точки О оси l.

Если угол между векторами е и а острый (рис. 50, а), то проекция вектора а на ось l равна длине отрезка ОА1 и где А1 — проекция точки А на прямую l.

Действительно,

Если угол между векторами е и а тупой (рис. 50,б), то проекция вектора а на ось l равна длине отрезка ОА1 и взятой со знаком минус.

В самом деле,

Если вектор а перпендикулярен оси l, то = 90° и прl а = | a | cos 90° = 0. Рассмотрим два важных свойства проекции вектора на ось.

Свойство 1. Для любых векторов а и b справедливо равенство прl (а + b) = прl а + прl b, где l — произвольная ось.

Это свойство позволяет заменять проекцию суммы векторов суммой их проекций и наоборот. Свойство 2. Для любого вектора а и любого числа k справедливо равенство

прl ka = k прl a,

где l — произвольная ось.

Это свойство позволяет выносить и вносить числовой множитель за знак проекции.

Справедливость этих свойств следует из правил действий над векторами, заданными своими координатами.

В самом деле, пусть l — произвольная ось с началом отсчета О и единичным вектором е. Введем прямоугольную систему координат следующим образом (рис. 51).

Примем точку О за начало координат, а вектор е — за первый базисный вектор (i = e). В качестве других базисных векторов j и k возьмем любые два единичных перпендикулярных друг другу вектора, лежащих в плоскости перпендикулярной оси l. Пусть вектор а = OA> имеет координаты х, у, z. Тогда, по определению проекции,

прl а = | a | cos .

Но | a | cos = x, т. е. проекция любого вектора на ось l равна абсциссе этого вектора в выбранном нами базисе.

Так как абсцисса суммы векторов равна сумме абсцисс слагаемых векторов (§ 11), то, следовательно, и проекция суммы векторов на ось l равна сумме проекций этих векторов на ось l.

Точно так же и проекция произведения вектора на число равна произведению этого числа на проекцию вектора, так как при умножении вектора на число его абсцисса умножается на это число.

2.Непрерывность функции. Свойства пределов от непрерывных функциях.

Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.

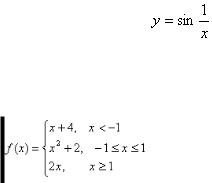
Тот же факт можно записать иначе:

Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.

Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию

f(x) = f(x0) + a(x)

где a(х) – бесконечно малая при х®х0. Свойства непрерывных функций.

1)Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.

2)Частное двух непрерывных функций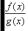 – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.

3)Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке. Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.