Билеты по математике / Билет 9
.pdf
Билет 9
1. Система линейных уравнений может быть представлена в матричной форме как:
или:
.
Здесь 
— это матрица системы, 
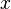— столбец неизвестных, а 
— столбец свободных членов. Если к матрице 
приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Однородные системы
Однородной системой линейных уравнений называется система вида:
Нулевое решение 
системы (1) называется тривиальным решением.
Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.
Если существует любое ненулевое решение системы, то оно называется нетривиальным.
Решения однородной системы обладают свойством линейности:
Теорема (о линейном решении однородных систем).
Пусть 
— решения однородной системы (1), 
—
произвольные константы. Тогда 
также является решением рассматриваемой системы.
Неоднородной системой линейных уравнений называется система вида:
— её расширенная матрица.
Теорема (об общем решении неоднородных систем).
Пусть 
(т.е. система (2) совместна), тогда:
если 
, где 
— число переменных системы (2), то решение (2) существует и оно единственно;
если 
, то общее решение системы (2) имеет вид
, где 
— общее решение системы (1), называемое
общим однородным решением,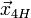 
— частное решение системы (2), называемое частным неоднородным решением.
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Гаусса требует 
арифметических операций.
Для системы 
линейных уравнений с 
неизвестными (над произвольным полем)
с определителем матрицы системы 
, отличным от нуля, решение записывается в виде
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
В этой форме формула Крамера справедлива без предположения, что 
отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов).
Можно также считать, что либо наборы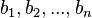 
и 
, либо набор 
состоят не из элементов кольца коэффициентов системы, а какого-нибудь
модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
2. Определение первообразной.
Первообразной функции f(x) на промежутке (a; b) называется такая функция
F(x), что выполняется равенство 
для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна
нулю, то справедливо равенство 
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Определение неопределенного интеграла.
Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается 
.
Выражение 
называют подынтегральным выражением, а f(x) –
подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом
интегрирования является не одна функция F(x), а множество ее первообразных
F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
1.
Производная результата интегрирования равна подынтегральной функции.
2.
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
3. |
, |
где |
k |
– |
произвольная |
константа. |
|
Коэффициент можно выносить за знак неопределенного интеграла. |
|||||
4.Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.